This document summarizes a thesis analyzing the static and dynamic finite element analysis of a composite leaf spring. The thesis examines a fiberglass-epoxy composite leaf spring used in a Chevrolet vehicle and explores its performance under heavier loads. Analytical calculations and FEA simulations are used to analyze stresses in the leaf spring and identify failures from increased loading. The results suggest reducing leaf spring thickness to lower delamination stresses at the mid-section from dynamic loading. Experimental validation and further studies of hybrid composites and eye-end design are recommended for future work.

1. STATIC AND DYNAMIC FEA ANALYSIS
OF A COMPOSITE LEAF SPRING
By
Himanshu Arun Raut
Thesis Advisor: Dr. Andrey Beyle
Thesis Defense Committee
Dr. Wen Chan, Dr. Kent Lawrence
Department of Mechanical and Aerospace Engineering

2. Contents
1. Introduction
2. Motivation and objective
3. Material properties
4. Geometry
5. Analytical calculations
6. Boundary Conditions & Simulation
7. Results
8. Conclusion
9. Future work
10. Acknowledgement
11. References

3. • Leaf springs function by absorbing the normal forces and vibration impacts due to
road irregularities by means of the leaf deflection and stored in the form of strain
energy for a short period of time and then dissipated.
• Steel leaf springs along with other alloys such as 55Si2Mn90 and similar type of cold
rolled steels have been used. Composites have been a suitable replacement for such
materials sue to several reasons.
• Firstly, Composites have a better elastic strain energy storage capacity
• Composites also have a high strength to weight ratio
• In addition to this composite leaf springs prevent sagging as in the case of steel leaf
springs which tend to make the ride more bumpy.
Introduction

4. Fig.1&2. Nomenclature of a leaf spring.
General arrangement of leaf spring over axle

5. • The objective of this study is to analyze the composite leaf spring structure that is
being manufactured by the industry for Chevrolet Corvette Grand model. The leaf
spring is made up of reinforced fiberglass epoxy.
• The composite leaf spring was designed to withstand forces incurred by weight of the
car(1500 Kgs=3300lbs. approx.) along with other external loads up to a certain limit.
• It was suggested that the same leaf spring may be used to support commercial light
tractor trailer. It was observed that the leaf sprig was unable to perform optimally as it
did for the automobile for the same load operating conditions.
• Delamination and micro-cracks started to appear on the central region where the leaf
spring is clamped to the axel.
Motivation and Objective

6. Motivation and Objective(contd..)
• We aim to show the cause of failure for the composite leaf spring by the use of finite
element simulations and by means of analytical calculations.
• Alternative designs and compatible material changes have been suggested in the later
part of the sections.

7. Fig3.Reinforced fiberglass epoxy composite leaf spring Fig4.Closeup of midsection

8. Material Properties
Composite
Material E1 (GPa) E2 (GPa) ν12 ν23 G12 (GPa) G23 (GPa)
Glass/Epoxy 61.401 13.454 0.259 0.436 5.362 4.685
Kevlar/Epoxy 108.276 3.814 0.34 0.246 2.119 1.531
Carbon/Epoxy 210.9 7.744 0.3 0.3 3.608 2.978
Material E1 (GPA) E2 (GPA) ν12 ν23 G12 (GPA) G23 (GPA)
Glass Fiber 85.5 85.5 0.23 0.23 35 35
Kevlar Fiber 151.17 4.1 0.35 0.15 2.9 1.782
Carbon Fiber 300 14 0.3 0.15 8 6.087
Epoxy Matrix 3 3 0.3 0.3 1.11 1.154
Table1. Anisotropic material properties calculated from fiber and matrix (calculated for 70% fiber)
Table2. Fiber and matrix material properties

9. Anisotropic material properties for composite are calculated by the following method
• Obtain the compliance matrix for the fiber and matrix C1 and C2
• Calculate for the two elements of compliances bij for the plane strain state for fiber and matrix.
• Calculate bulk moduli K23 for the fiber and matrix
• Calculate the effective elastic properties of the Unidirectional composite
• Substitute values of the effective elastic properties for the composite material in the compliance matrix
• Calculate the inverse of this compliance matrix
ν12
𝐸1
=
ν21
𝐸2
ν13
𝐸1
=
ν31
𝐸3
ν23
𝐸2
=
ν32
𝐸3

10. Geometry
Fig.5 drawings for front views of leaf spring assembly

11. Fig.6 drawings for front and top views of clamp and bushing

12. Analytical calculations
Calculations are performed under the following assumptions
1. The leaf spring is a part of a circular ring and possesses symmetry
2. The leaf spring is made up of linier anisotropic material and the pole is located at the center
of the two circles
3. The angle between the applied force and the transversal axis is 0°
4. Bending of the linearly anisotropic curved beam occurs due to the application of end force
which is applied at the center of the cross section
Note: All calculations are performed on PTC Mathcad Prime 3.1. Please refer reference [8]

13. Analytical calculations for radial ,normal and shear stresses [1]
Fig.6 reference [1]

14. Reference [2]

15. Radial Stresses (MPa)
Radius 766 768 770 772 774 776 778 780 782 784 786
Thetaθ
0 0 0 0 0 0 0 0 0 0 0 0
1 0 0.054 0.095 0.124 0.141 0.146 0.139 0.121 0.092 0.051 0
2 0 0.107 0.19 0.248 0.281 0.292 0.279 0.242 0.184 0.103 0
3 0 0.161 0.284 0.371 0.422 0.437 0.418 0.364 0.276 0.154 0
4 0 0.214 0.379 0.495 0.562 0.583 0.557 0.485 0.367 0.206 0
5 0 0.268 0.473 0.618 0.703 0.728 0.696 0.606 0.459 0.257 0
6 0 0.321 0.568 0.741 0.843 0.873 0.843 0.726 0.551 0.308 0
7 0 0.374 0.662 0.864 0.983 1.018 0.973 0.847 0.642 0.359 0
8 0 0.427 0.756 0.987 1.122 1.163 1.111 0.967 0.733 0.41 0
9 0 0.481 0.85 1.109 1.261 1.307 1.248 1.087 0.824 0.461 0
10 0 0.533 0.943 1.232 1.4 1.451 1.386 1.206 0.915 0.512 0
11 0 0.586 1.036 1.353 1.539 1.594 1.523 1.326 1.005 0.562 0
12 0 0.639 1.129 1.475 1.677 1.737 1.659 1.444 1.095 0.613 0
13 0 0.691 1.222 1.595 1.814 1.88 1.795 1.563 1.185 0.663 0
14 0 0.743 1.314 1.716 1.951 2.022 1.931 1.681 1.274 0.713 0
15 0 0.795 1.406 1.836 2.087 2.163 2.066 1.798 1.363 0.763 0
16 0 0.847 1.497 1.955 2.223 2.303 2.2 1.915 1.452 0.812 0
17 0 0.898 1.588 2.074 2.358 2.443 2.333 2.031 1.54 0.862 0
18 0 0.949 1.679 2.192 2.492 2.582 2.466 2.147 1.627 0.911 0
19 0 1 1.768 2.309 2.625 2.721 2.595 2.262 1.715 0.96 0
20 0 1.051 1.858 2.426 2.758 2.858 2.73 2.376 1.801 1.008 0
21 0 1.101 1.947 2.542 2.89 2.995 2.86 2.49 1.887 1.056 0
22 0 1.151 2.035 2.575 3.021 3.13 2.99 2.603 1.973 1.104 0
Table3.
Analytical results

16. 0
0.5
1
1.5
2
2.5
3
3.5
766 768 770 772 774 776 778 780 782 784 786
RadialStresses(MPa)
Radius (mm)
Fig7. Radial stress are highest for θ=22° radius 776mm
θ=22°

17. Fig8. Radial stress for curved
section plane
Fig9. Radial stress for
mid section plane

18. Fig10.

19. θ
Analytical
Radial stresses
(MPa)
Computational
Radial Stresses
(MPa)
% error
0 0 0 0
2 0.292 0.527 44.6
4 0.583 0.606 3.795
6 0.873 0.89 1.91
8 1.163 1.174 0.93
10 1.451 1.45 0.07
12 1.737 1.73 0.4
14 2.022 2.112 4.26
16 2.303 2.28 1.009
18 2.582 2.537 1.744
20 2.858 2.927 2.357
22 3.13 2.988 4.75
Computational and Analytical Results
Comparison
0
0.5
1
1.5
2
2.5
3
3.5
0 5 10 15 20 25
RADIALSTRESSES(MPa)
θ
-
Analytical data Comptational daata
Table4. Radial stress at r = 766mm Fig11.

20. Boundary conditions and simulations
rot z = free
rot x, y=0
x, y, z=0
rot z = free
rot x, y=0
x = free
y, z=0
A remote mass of 375 Kg is attached at the center of the bottom face to promote forced
vibrations.
Fig12. boundary conditions

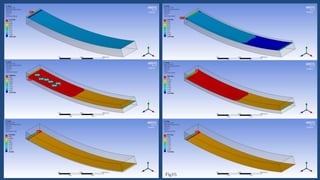
21. Meshing has been done by using body sizing and by use of hex dominant method with element
type as all quad. Mid side element nodes are selected to KEPT. This generates a mesh with brick
elements particularly SOLID 186. SOLID186 is a higher order 3-D 20-node solid/brick element.
The middle mesh was generated using sphere of influence[3]
Fig13. Meshing for geometry Fig14. Meshing element reference [3]

22. 0
10
20
30
40
50
60
70
80
7 10 15 30
Deformationsinmm
Loads in KN
Deflections
fiberglass epoxy kevlar epoxy carbon epoxy
Static Analysis Results
7 10 15 30
RadialStresses(MPa)
Loads KN
RADIAL STRESSES
glass epoxy kevlar epoxy carbon epoxy
Fig15. Fig16.

23. 0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
80.00
90.00
100.00
0.00 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60
DEFORMATION(MM)
TIME IN SECONDS
DEFLECTION
Reinforced fiberglass epoxy Kevlar epoxy Carbon Epoxy
Transient Analysis Results
Fig15.
Vid1.

24. 0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
8.00
9.00
0.00 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60
RADIALSTRESSES(MPa)
TIME IN SECONDS
RADIAL STRESSES
glass epoxy kevlar epoxy carbon epoxy
Fig16a,b,c,d

25. Vid1.

26. Varying thickness model results fiberglass epoxy
Fig17.
(a) Model for thickness 22 mm (b) Model for thickness 18 mm

27. Varying thickness model results fiberglass epoxy
Fig18.
(a) Model for thickness 22 mm (b) Model for thickness 24 mm

28. • When the spring constant is low the effective force decreases thereby reducing the radial
and shear stresses
• Since k is proportional to the thickness, the reduction of the spring constant will mean
reducing the thickness of the leaf spring.
• This will result in increase in the tensile and compressive stresses on the top and bottom
faces of the leaf spring
• Here the objective is to compromise the thickness that moderates the level of
delamination stresses with tensile and compressive stresses in a safe level

29. • The reinforced fiberglass epoxy fails doe to delamination stress built up specifically in the mid
section
• The deflection due to dynamic loading induces tensile forces on the laminate layers.
• This results in tensile radial stress built up along with inter laminar shear stresses.
• The leaf spring model can be improved by changing the design as illustrated in the results
section.
• The thickness of the leaf spring needs to be reduced in order to minimize the delamination
stresses (σr)max
Conclusion

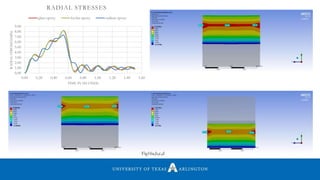
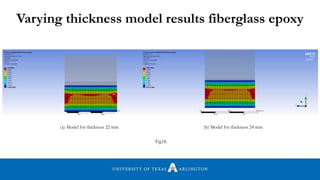
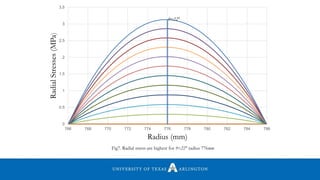
30. 2
2.5
3
3.5
4
4.5
1.02 1.021 1.022 1.023 1.024 1.025 1.026 1.027
(σr)max(Mpa)
b/a
DELAMINATION STRESS(σr)max
Fig19. Delamination stresses (σr)max as a function of b/a for β=3.568
Reference [2]

31. • Experimental study can be performed for the same model to validate the result using 3 point
and 4 point bend set up
• Eye end design can be studied to reduce the chances of local delamination due to
concentration of interlaminar shear stress.[@]
• Hybrid composites can be used as study material for heavy axel loadings
Future Work
Reference [4]
Fig20.

32. Acknowledgement
• I would like to thank Dr. Andrey Beyle for his inspiring guidance, encouragement and for
investing his valuable time in mentoring me.
• I would also like to thank the committee members who are present here for giving their valuable
time and opinion.
• In the end I would like to thank my colleagues and friends who help me along the way

33. References
1. Lekhnitskii, S.G.; Tsai, S.W.; and Cherom, T.: Anisotropic plates. Gordon and Breach Science
Publishers, New York, 1968
2. ANSYS Documentation > Mechanical APDL > Element Reference > I. Element Library >
SOLID 186
3. William L. Ko, T.: Delamination Stresses in Semicircular Laminated Composite Bars Jan 1988
NASA
4. Shokrieh MM, Rezaei D. Analysis and Optimisation of composite leaf springs. Comp Struct
2003;60:317-25

34. Thank You!
Questions?