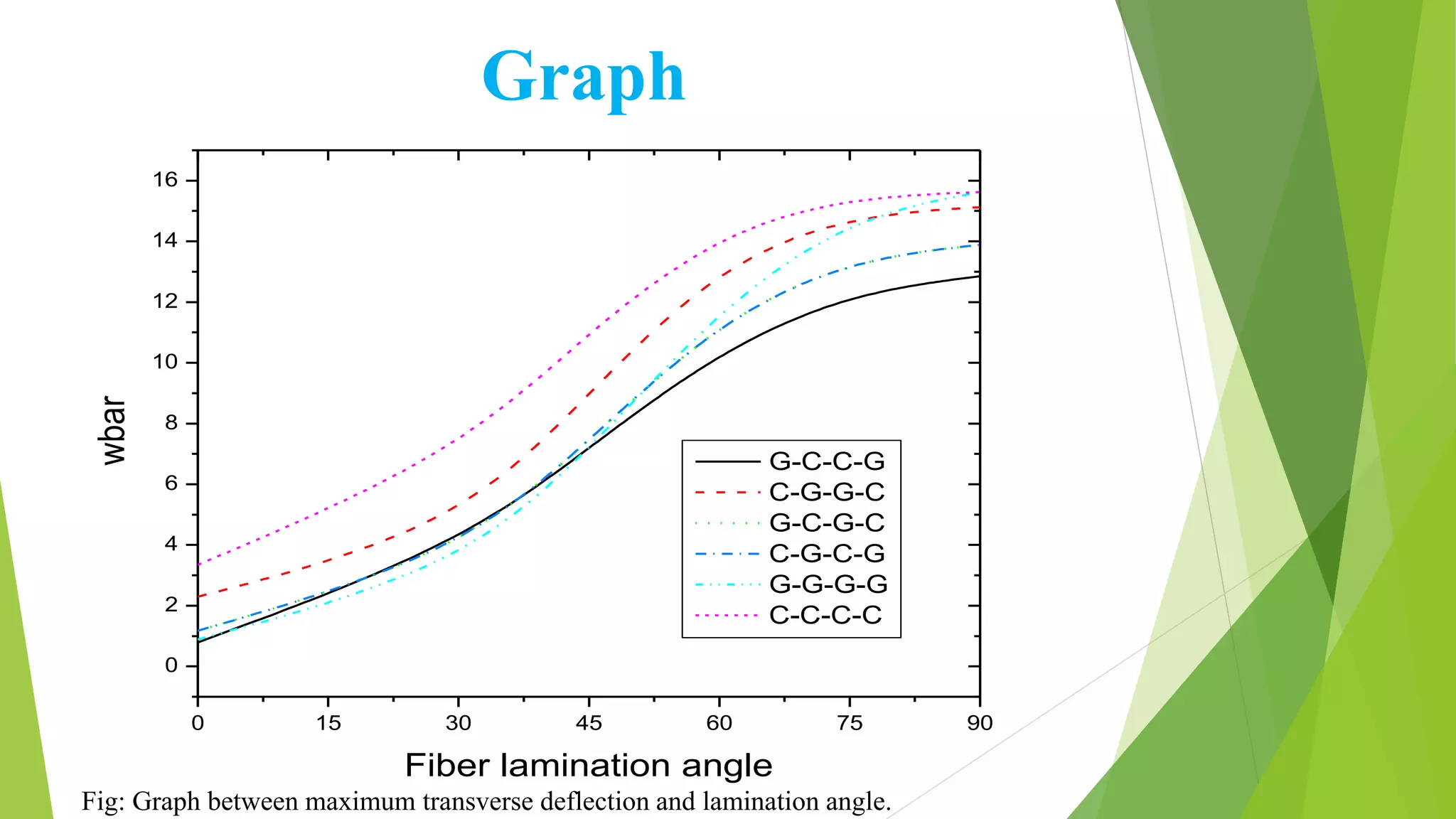
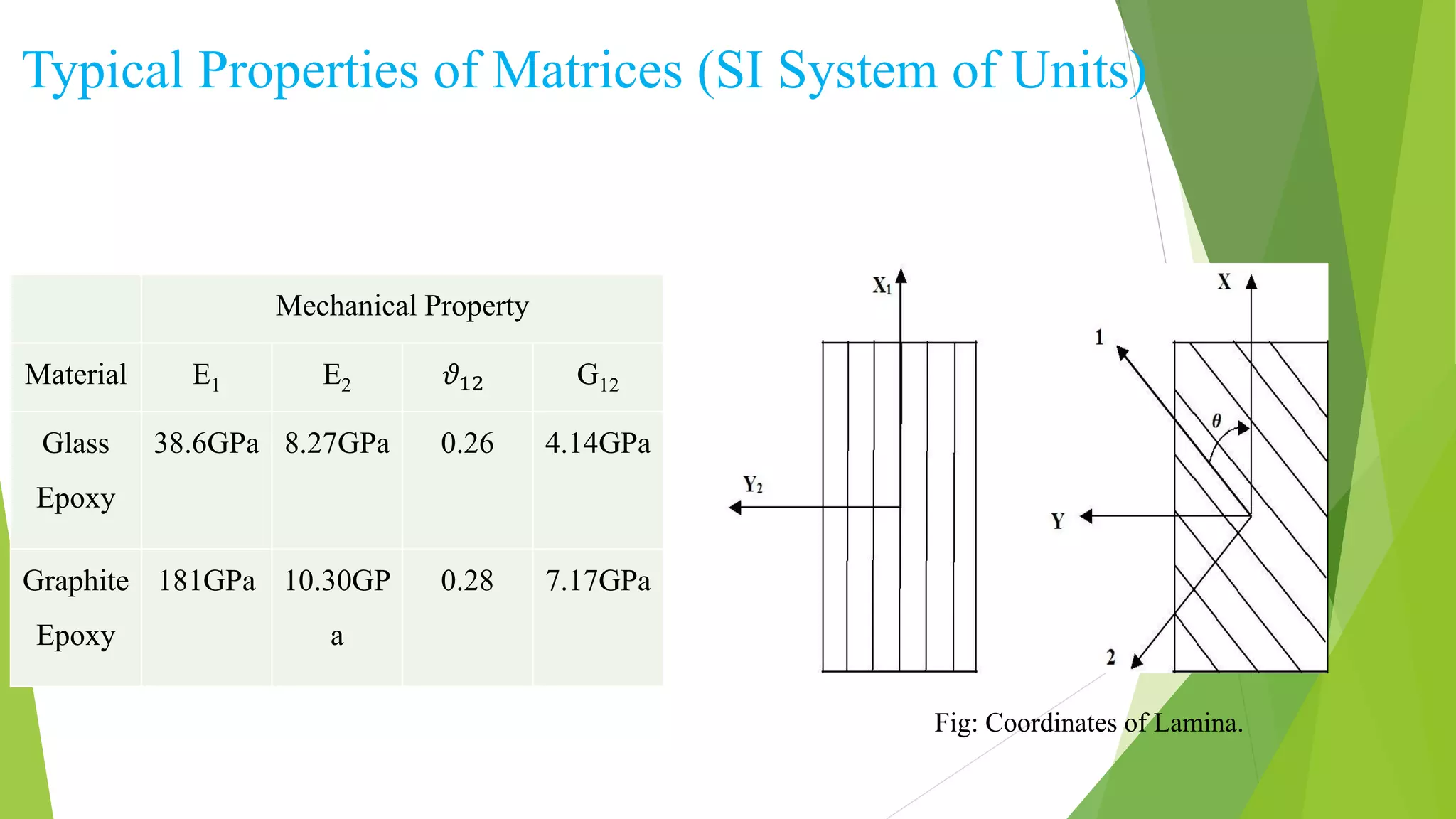
The seminar report investigates the impact of lamination angles on the maximum deflection of simply supported composite beams, specifically made of glass-epoxy materials. It details the methods used for analysis, including classical laminated beam theory and MATLAB simulations, and finds that the g-c-c-g arrangement of composite materials yields the minimum transverse deflection. Conclusions drawn highlight the effectiveness of this arrangement in practical applications and suggest future studies to explore variations in beam types and loading conditions.

1. A Seminar Report on
“Study of the Effect of Lamination angle on
maximum deflection of simply supported
composite beam”
Under the Guidance of
Mr Arnab Choudhary
(ASSISTANT PROFESSOR)
MECHANICAL ENGINEERING
DR. B C ROY ENGINEERING COLLEGE
DURGAPUR

2. Slide Plan
1. Composite material
2. Fibre matrix
3. Classification of laminates
4. Advantages
5. Applications
6. Literature Review
7. Problem Outline
8. Approach to the problem
9. Laminate Constitutive Equation
10. A B D Matrix
11. Beam Equation
12. Symmetric Beams
13. Deflection
14. Typical Properties of Matrices (SI System
of Units)
15. Result
16. Discussion Of Results
17. Conclusion
18. Future Work
19. Reference

3. Composite Material
Definition
 A Composite material is a material system composed of two or more macro constituents that
differ in shape and chemical composition and which are insoluble in each other.
 Made from two or more constituent materials
 Materials having significantly different physical or chemical properties.
 Produced material have different characteristics from the individual components.

4. Fibre and Matrix
 Fibre reinforced composite materials consists of fibres of significant strength and
stiffness embedded in a matrix with distinct boundaries between them. Both fibres and
matrix maintain their physical and chemical identities, yet their combination performs a
function which cannot be done by each constituent acting singly.
 Fibres convey structural stiffness and strength to GRP (glass reinforced plastic)
materials. The matrix transfers the load between the fibres and also supports them under
compression loading.

5. Classification of Laminates
 Symmetric Laminates:
A laminate is called symmetric when the material, angle and thickness of the layers are
the same above and below the mid-plane.
 Anti-symmetric Laminates:
A laminate is called anti-symmetric when the material and thickness of the plies are
same above and below the mid-plane but the orientation of the plies at same distance
above and below the mid-plane have opposite signs.

6. Advantages
 Good inplane stiffness and strength.
 Low density.
 Relatively low cost.
 Corrosion resistance.
 Low coefficient of thermal expansion.
 Relatively mature technology.
 Excellent in-service experience.
 Compared with metals, the principal advantages of
advanced composites in aerospace applications are their
superior specific strength and stiffness,
6

7. Applications
 1. Marine field
 2. Aircraft and Space
 3. Automotive
 4. Sporting goods
 5. Medical Devices
 6. Commercial applications

8. Literature Review
 In an early study on composite by Barbero et al. focused on
ultimate bending strength of composite beams under bending. The
study compared the experimental and analytical solution and
found that glass fibre reinforced plastic (GFRP) beam attained
ultimate bending strength as the result of local buckling of the
compression in flange.
 In another study on composite rectangular beams, Chandra and
Chopra presented a comparative study of experimental and
theoretical data to understand the static response on composite
rectangular beams.

9. Problem Outline
A simply supported laminated composite beam of length 0.2m
and width of 6mm made of glass epoxy material in considered for
study angle ply antisymmetric arrangement of the lamina are
considered. A uniform load of 400N/m is applied on the beam.
Maximum deflection of the beam is calculated for different
lamination angle. The main objective of the paper is to find out the
lamination angle at which minimum deflection is obtained & to final
out the effect at lamination angle on maximum at beam deflection.

10. Approach to the problem
 A mathematical model is built up using classical laminated
beam theory (CBT).
 To find out the maximum deflection of simply supported
beam subjected to uniformly distributed load (UDL) for
different material.
 Maximum deflection is calculated for different laminated
angle by formulating a program in MATLAB software.
 The study is intended to provide tools that ensure better
designing options for composite laminate.

11. Laminate Constitutive Equation
• Stress-Strain Relationship for 𝜃 Lamina
The stress-strain relationship for thin lamina in the matrix form along the global x-y axis is given as
𝜎𝑥
𝜎 𝑦
𝜏 𝑥𝑦
=
𝑄11 𝑄12 𝑄16
𝑄21 𝑄22 𝑄26
𝑄61 𝑄62 𝑄66
𝜀 𝑥
𝜀 𝑦
𝛾𝑥𝑦
• Constitutive Equation of Laminated Plate
The stresses in the 𝑘 𝑡ℎ
ply at a distance of 𝑍 𝑘from the reference plane in terms of strains and laminate
curvatures can be expressed as
𝜎𝑥
𝜎 𝑦
𝜏12 𝑘 𝑡ℎ
=
𝑄11 𝑄12 𝑄16
𝑄21 𝑄22 𝑄26
𝑄61 𝑄62 𝑄66 𝑘 𝑡ℎ
𝜀 𝑋
𝑂
𝜀 𝑌
𝑂
𝛾 𝑋𝑌
𝑂
+ 𝑍𝑥
𝐾 𝑋
𝐾𝑦
𝐾12

12. A B D Matrix
The total constitutive equation or load-deformation relations for the laminate is as follows
𝑁
𝑀
=
𝐴 𝐵
𝐵 𝐷
𝜀0
𝐾
Where
𝐴 = 𝑄 𝑘
ℎ 𝑘 − ℎ 𝑘−1
𝑛
𝑘=1
𝐵 =
1
2
𝑄 𝑘
𝑛
𝑘=1
ℎ 𝑘
2
− ℎ 𝑘−1
2
𝐷 =
1
3
𝑄 𝑘
(
𝑛
𝑘−1
ℎ 𝑘
3
− ℎ 𝑘−1
3
)

13. Beam Equation
The bending stress in an isotropic beam under an applied
bending moment, M , is given by,
σ =
𝑀𝑧
I
where
z= Distance from the centroid
I= Second moment of area
𝜎= Bending stress
M= Bending moment

14. Symmetric Beams
 To keep the introduction simple, we will discuss beams that are symmetric
and have a rectangular cross-section.
 Because the beam is symmetric, the loads and moments are decoupled
𝑀 𝑥
𝑀 𝑦
𝑀 𝑥𝑦
= 𝐷
𝐾𝑥
𝐾 𝑦
𝐾𝑥𝑦
or
𝐾𝑥
𝐾 𝑦
𝐾𝑥𝑦
= 𝐷 −1
𝑀 𝑥
𝑀 𝑦
𝑀 𝑥𝑦
Now, if bending is only taking place in the x direction then
𝑀 𝑌 = 0 , 𝑀 𝑥𝑦 = 0
That is
Kx = D11Mx
Ky = D12Mx
KXY = D16Mx

15. Deflection
To find the maximum deflection of the beam, 𝛿 we use the isotropic beam
formula:
𝑊𝑚𝑎𝑥 =
5𝑞𝐿4
384 𝐸 𝑥𝑥 𝐼 𝑦𝑦
Where,
q = Load Intensity (N/m)
L = Length of the beam (m)
𝛿 = Deflection of the beam
𝐸 𝑥 𝑥 =Effective bending modulus of beam
Iyy = second moment of area with respect to the x–y –plane

16. Non dimensional transverse deflection,
𝑤 = 𝑤 𝑚𝑎𝑥(𝐸2ℎ3
𝑞0 𝑎4
) ∗ 102
𝑊 =
𝑊𝑚𝑎𝑥 × 8.27 × 109 × ℎ3 × 𝑏
𝑞𝐿4 × 100

17. Typical Properties of Matrices (SI System of Units)
Mechanical Property
Material E1 E2 𝜗12 G12
Glass
Epoxy
38.6GPa 8.27GPa 0.26 4.14GPa
Graphite
Epoxy
181GPa 10.30GP
a
0.28 7.17GPa
Fig: Coordinates of Lamina.

18. Result
Wbar for different material arrangement
ARRANGEMENT
LAMINATION ANGLE
G-C-C-G C-G-G-C G-C-G-C C-G-C-G G-G-G-G C-C-C-C
[±0]
0.7918 2.2911 1.1768 1.1768 0.8892 3.3476
[±30]
3.9791 4.5605 3.6844 3.6844 3.2126 6.9985
[±45]
7.2019 9.0034 7.4395 7.4395 7.0851 11.0671
[±60]
10.4028 13.2527 11.414 11.414 11.8315 14.3012
[±75]
12.2993 14.8525 13.401 13.401 14.7884 15.4477
[±90]
12.8528 15.1215 13.8788 13.8788 15.625 15.625
Maximum deflection of simply supported composite beam at different lamination angle for
different combination of composite material.

19. Graph
0 15 30 45 60 75 90
0
2
4
6
8
10
12
14
16
wbar
Fiber lamination angle
G-C-C-G
C-G-G-C
G-C-G-C
C-G-C-G
G-G-G-G
C-C-C-C
Fig: Graph between maximum transverse deflection and lamination angle.

20. • Graph shows the effect of fibre lamination angle on transverse deflection of beam.
• It is observed that as the lamination angle increases from ± 0° to ± 90° transverse deflection
increases.
• Maximum deflection obtained at ±90° and minimum deflection obtained at ± 0°. Transverse
deflection is obtained for different combination of composites material.
• It is find out from the graph that G-C-C-G combination of composite material experience the
minimum transverse deflection as compared to other combination of composite material.
• Graphite has more strength than glass as well as modulus of elasticity of graphite is higher than
glass that makes graphite more strengthened and glass softer.
Discussion Of Results

21. Conclusion
 It is concluding that the best arrangement of composite material is G-C-C-G. So it canbe
used for different practical application.
 G-C-C-G arrangement facilitates reliable service as there is minimum transvers deflection
obtained among all of the arrangement.
 An analytical method was developed for deflection analysis of a composite rectangular
beam.
 A graph is plotted between Deflection & Lamination angle.
 An analytical method is purposed to evaluatetransverse deflections of composite beam with
simply supported arrangement. MATLAB CODES are used to implement the analytical
expressions that are derived.
 From the study it is concluded that as the lamination angle changes to ± 0° to ± 90°
transverse deflection increases.
 Maximum transverse deflection is obtained at ± 90° and minimum transverse deflection
obtained at± 0°.
21

22. Future Work
 Further calculation can be made for deflection with different types of beam such as
cantilever beam, overhanging bean, fixed beam, and different types of load condition
such as point load, uniformly varying loadetc.
 By taking some different composites material deflection can be obtained.
 Calculation to be made by considering some other parameters such as maximum stress
developed.
 Maximum transverse deflection can also be obtained by using ANSYS software and
compared with result obtained from analytical method

23. References
 Autar K. Kaw “Mechanics of Composite Materials”, Second
edition, 2006, pp. 431-445
 J.N.Reddy “Mechanics of Laminated Composite Plates and Shells
Theory and Analysis”, Second Edition, 200, pp. 10-48
 Barbero, E. J., Fu, S. H., and Raftoyiannis, I. “Ultimate bending
strength of composite beams.” Journal of Materials in Civil
Engineering Vol.3 No.4, 1991, pp. 292–306.
 Chandra, R., and Chopra, I., “Experimental and theoretical
analysis of composites I-beams with elastic couplings”, AIAA
Journal Vol. 29 No.12, 1991, pp. 2197–2206.