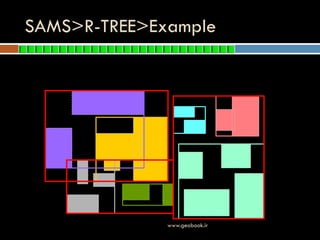
This document discusses spatial indexing methods for geographic data. It begins by defining indexes and their purpose for improving data access times. It then describes two main types of spatial indexes: point access methods (PAMs) like grid files, kd-trees, z-ordering, and B-trees; and spatial access methods (SAMs) like the R-tree. The document focuses on R-trees, explaining their structure, algorithms for searching, inserting and deleting data, and variations like the R*-tree that further optimize performance. It concludes by listing references for additional information on spatial indexing techniques.

1. EMAIL : MOH3N.RASHIDIAN@gmail.com
TEL :(+98) 9378812726
IN THE NAME OF ALLAH
PRESENTOR: Mohsen Rashidian
www.GeoBook.ir
CONTACT INFO:
www.geobook.ir
SPATIAL INDEXING

2. PREDICTED TIME : 30 MIN
SLIDE NOM:41
SUBJECT:
SPATIAL INDEXING
EMAIL
www.geobook.ir

3. CONTENTS…
 What is an index?
 Main index types…
 Point access methods(PAMS)…
 Spatial access methods(SAMS)…
 R-TREE issues
 Summary
 References
www.geobook.ir

4. What is an index?
 Concept of an index:
“auxiliary file to search a data file“
 index records have
•key value
•address of relevant data sector (arrows)
 In general indices improve access time but may cause deletion
And insertion data items
can increase processing time!
www.geobook.ir

5. An index in general…
 Assume we have some files…
In computer science 4 ways are exist:
1-pile records
2-fixed size records
3-sequential records
4-indexed sequential
No meaningful sequence
worst access time
best insertion time
better access time(fixed size)
Still best insertion time
Ordered by a key sequence value
good access time
Low speed insertion time(to keep sequence order)
Include the primary data area and an indexed area
good access time
Good insertion time(may need to refer indexed area)
www.geobook.ir

6. Main index types
 Point access methods(PAMs)
i. Grid File
ii. kd-tree based
iii. Z-ordering
iv. B-tree
 Spatial access methods(SAMS)
i. R-TREE(R*-tree, Hilbert R-tree)
www.geobook.ir

7. Point access methods(PAMS)
 PAM: index only point data
Multidimensional Hashing(grid files)
Hierarchical (tree-based) structures (kd-tree)
Space filling curve(z-ordering or quad-tree)
 The problem
Given a point set and a rectangular query, find the points enclosed in the
query
www.geobook.ir

8. PAMS>Grid File
 Idea: Use a grid to partition the space each cell is
associated with one page
 Exponential growth of the directory
 implementation
Grid array:
2 dimensional array with pointers to
buckets G(0,…, nx-1, 0, …, ny-1)
Linear scales:
Two 1 dimensional arrays that used to
access the grid array X(0, …, nx-1),
Y(0, …, ny-1)
www.geobook.ir

9. PAMS>Grid File>Example
Linear scale X
Linear scale
Y
Grid Directory
Buckets/Disk
Blocks
www.geobook.ir

10. PAMS>KD-TREE
 kd-tree is a main memory binary tree for indexing
k-dimensional points
 Storing in external memory is tricky
 At each level we use a different dimension
 kd-tree is not necessarily balanced
A
B
C
DE
x=5
y=6
x=6
Y=3
www.geobook.ir

11. X=5
y=5
y=6
x=3
y=2
x=8 x=7
X=5 X=8
X=7
Y=6
Y=2
Y=5
X=3
PAMS>KD-TREE>Example
www.geobook.ir

12.  Map points from 2-dimensions to 1-dimension
 Basic assumption:
Finite precision in the representation of each co-ordinate, K bits
(2K values)
 The address space is a square (image) and represented as a
2K x 2K array
 Each element is called a pixel
PAMS> Z-ordering
www.geobook.ir

13. PAMS> Z-ordering
 Impose a linear ordering on the pixels of the
image  1 dimensional problem
00 01 10 11
00
01
10
11
A
ZA = shuffle(xA, yA) = shuffle(“01”, “11”)
= 0111 = (7)10
www.geobook.ir

14. PAMS> Z-ordering for Regions
 Break the space into 4 equal quadrants: level-1 blocks
 For a level-i block: all its pixels have the same prefix up to
2i bits; the z-value of the block
www.geobook.ir

15.  Object is recursively divided into blocks until:
 Blocks are homogeneous
 Pixel level
 Quadtree: ‘0’ stands for S and W
‘1’ stands for N and E
00 01 10 11
00
01
10
11
SW
SE
NW
NE
1100
10
01
11
1001
1011
PAMS> Quad tree
www.geobook.ir

16. Quad tree(2D)
00 01 10 11
00 01 10 11
00 01
10 11
00 01
10 10
www.geobook.ir

17. Quad-tree(3D) or Oc-tree
010 011 100 101000 001 110 111
010 011 100 101000 001 110 111
000 001
010 011
100 101
110 111
www.geobook.ir

18. PAMS>B-TREE
 Good access time
 Reasonable sequential read on the sequence key
 Insertion and deletion do not damage the balance
of the tree
www.geobook.ir

19. Spatial access methods(SAMS)
 Indexes for spatial data that have extend (not only
point data)
 Use only Minimum Bounding Rectangles –MBRs
(filtering)
 R-tree (Guttman, 1984) is the prominent SAM
 Implemented in Oracle, Postgres, Informix
www.geobook.ir

20.  2-dimensional version of the B-tree!
SAMS>R-TREE
 Can store:
i. a set of polygons (regions of a subdivision)
ii. a set of polygonal lines (or boundaries)
iii. a set of points
iv. a mix of the above
 Stored objects may overlap
www.geobook.ir

21. SAMS>R-TREE
 Originally by Guttman, 1984
 Dozens of variations and optimizations since
 Suitable for windowing, point location and intersection
queries
Every internal node contains entries (rectangle, pointer to child node)
All leaves contain entries (rectangle, pointer to object) in database or file
Rectangles are minimal bounding rectangles (MBR)
Definition R-tree:
www.geobook.ir

22. SAMS>R-TREE>Grouping of objects
 Objects close together in same leaves
⇒ small rectangles ⇒ queries descend in only few subtrees
 Group the child nodes under a parent node such that small
rectangles arise
www.geobook.ir

23. Heuristics for fast queries
 Small area of rectangles
 Small perimeter of rectangles
 Little overlap among rectangles
 Good access time
 Reasonable amount of insertion and deletion does not cause
tree reconstraction
 Height number of deletion and insertion requires restruction
of tree
www.geobook.ir

24. SAMS>R-TREE>Example
www.geobook.ir

25. SAMS>R-TREE>Example
www.geobook.ir

26. SAMS>R-TREE>Example
www.geobook.ir

27. SAMS>R-TREE>Example
www.geobook.ir

28. SAMS>R-TREE>Example
www.geobook.ir

29. SAMS>R-TREE>Example
point containment
query
www.geobook.ir

30. SAMS>R-TREE>Example
point containment
query
www.geobook.ir

31. SAMS>R-TREE>Searching
 Q is query object (point, window, object)
 For each rectangle R in the current node,
 if Q and R intersect,
 search recursively in the subtree under the pointer at R (at an
internal node)
 get the object corresponding to R and test for intersection with R
(at a leaf)
www.geobook.ir

32. SAMS>R-TREE>Inserting
 Determine minimal bounding rectangle (MBR) of new object
 When not yet at a leaf (choose subtree):
i. determine rectangle whose area increment after insertion of R is
smallest
ii. increase this rectangle if necessary and insert R
 At a leaf:
i. if there is space, insert, otherwise Split Node
New MBRs
Split Node
www.geobook.ir

33. SAMS>R-TREE>Deletion
 Find the leaf (node) and delete object; determine new
(possibly smaller) MBR
 If the node is too empty (< m entries):
i. delete the node recursively at its parent
ii. insert all entries of the deleted node into the R-tree
 Note: Insertions of entries/sub-trees always occurs at the level
where it came from
www.geobook.ir

34. SAMS>R-TREE>Deletion>Example
Should deleted
www.geobook.ir

35. SAMS>R-TREE>Deletion>Example
www.geobook.ir

36. SAMS>R-TREE>Deletion>Example
www.geobook.ir

37. SAMS>R-TREE>Deletion>Example
www.geobook.ir

38. SAMS>R-TREE>Deletion>Example
www.geobook.ir

39. R*-TREES!
 Is there any other property that can be optimized?
R*-tree  Yes!
 Optimization Criteria:
i. Area covered by an index MBR
ii. Overlap between directory MBRs
iii. Margin of a directory rectangle
iv. Storage utilization
 Sometimes it is impossible to optimize all the above
criteria at the same time!
www.geobook.ir

40. REFRENCES…
 H. V. Jagadish: Linear Clustering of Objects with Multiple Atributes. ACM SIGMOD
Conference 1990: 332-342
 Walid G. Aref, Hanan Samet: A Window Retrieval Algorithm for Spatial Databases
Using Quadtrees. ACM-GIS 1995: 69-77
 A. Guttman (1984). R-trees: A dynamic index structure for spatial searching. Proc. A
CM SIGMOD Int. Conf. on Management of Data, pages 47-57.
 Oracle Spatial 10g White Paper (2006). Oracle Spatial Quadtree Indexing, 10g
Release 1 (10.1).
‫ﭘﻭﺭﻑ‬ ‫ﺣﮑﻳﻡ‬.1388‫ﺩﺭﺱ‬ ‫ﮐﻼﺳﯽ‬ ‫ﺟﺯﻭﻩ‬“‫ﻣﮑﺎﻧﯽ‬ ‫ﺩﺍﺩﻩ‬ ‫ﭘﺎﻳﮕﺎﻩ‬“‫ﺑﺧﺵ‬DATA INDEXING‫ﺩﻭﺭﻩ‬
‫ﺍﺭﺷﺩ‬ ‫ﮐﺎﺭﺷﻧﺎﺳﯽ‬GIS‫ﮐﺭﻣﺎﻥ‬ ‫ﺻﻧﻌﺗﯽ‬ ‫ﺩﺍﻧﺷﮕﺎﻩ‬.
www.geobook.ir

41. www.geobook.ir