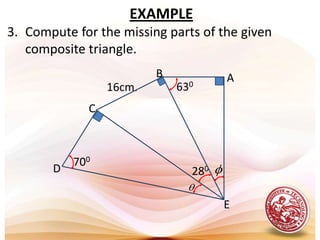
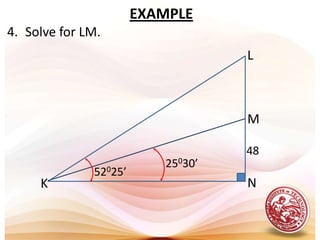
1. Solving right triangles involves sketching the triangle, identifying given and unknown parts, and using trigonometric functions, the Pythagorean theorem, or angle relationships to calculate unknowns. 2. Angles of elevation are formed between an observer's line of sight above the horizontal, while angles of depression are below the horizontal. These can be used to calculate heights or distances. 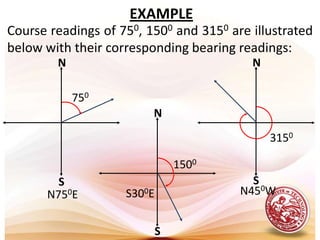3. Bearing is the acute angle from north or south, while course is the clockwise angle from north along the line of travel. These specify directions.

1. SOLUTIONS OF RIGHT TRIANGLE

2. SOLUTION OF RIGHT TRIANGLE Solving a triangle means determining the measures of all sides and angles of the triangles. In solving problems involving right triangle, the following steps may be considered:Sketch the required triangle as accurate as possible based on the given data.

3. Identify the given and the required parts of the triangle.

4. Solve for the unknown parts of the triangle using any of the following:The definitions of the trigonometric functions.b) The Pythagorean relations.c) The relation of complimentary angles.

5. EXAMPLE 1. Solve the following triangles, in which C = 900:a = 35 , c = 92b) A = 29030’ , b = 72.82. Compute for the length of AD.AB8 cm.480C72010’D

6. EXAMPLE 3. Compute for the missing parts of the given composite triangle.BA63016cm.C700D280E

7. EXAMPLE 4. Solve for LM.LM4825030’52025’NK

8. ANGLES OF ELEVATION AND DEPRESSION If an observer sights an object, the angle formed between a horizontal line and his line of sight is called the angle of elevationif the line of sight is above the horizontal and the angle of depression if the line of sight is below the horizontal.Object Line of sightAngle of ElevationHorizontal LineObserver Angle of DepressionLine of sightObject

9. EXAMPLE If the angle of elevation of the top of the tower is 52031’. Find the height of the tower if the observer is 41.5 m. from its base.2. Find the angle of elevation of the sun if the shadow of the pole 60 ft. tall and reaches 90 ft. from the pole.3. From the top of a lighthouse 30 m. high, the angle of depression of a boat in the sea was 28045’. How far was the boat from the top and base of lighthouse?

10. EXAMPLE 4. From a window Carlo observes the lamp post. He noted that the angle of elevation of its top is 43020’ while the angle of depression of its base is 20015’. If the top of the lamp post is 30 m. away from the window and its base is 25 m., what is the height of the lamp post?5. From where he stands 75 ft. away from the tree, a mountaineer 6 ft. tall, found that the angle of elevation of the top of the tree was 37025’. Find the total height of the tree.

11. DIRECTION OF ANGLES There are two ways in which the direction of an angle can be determined. They are bearing and course.Bearing is an acute angle measured from due north or due south. The North-South line is the basis of the acute angle measurement.Course is the angle measured clockwise from north to the line of travel.

12. EXAMPLE Course readings of 750, 1500 and 3150 are illustrated below with their corresponding bearing readings:NN750N31501500SSN450WS300EN750ES