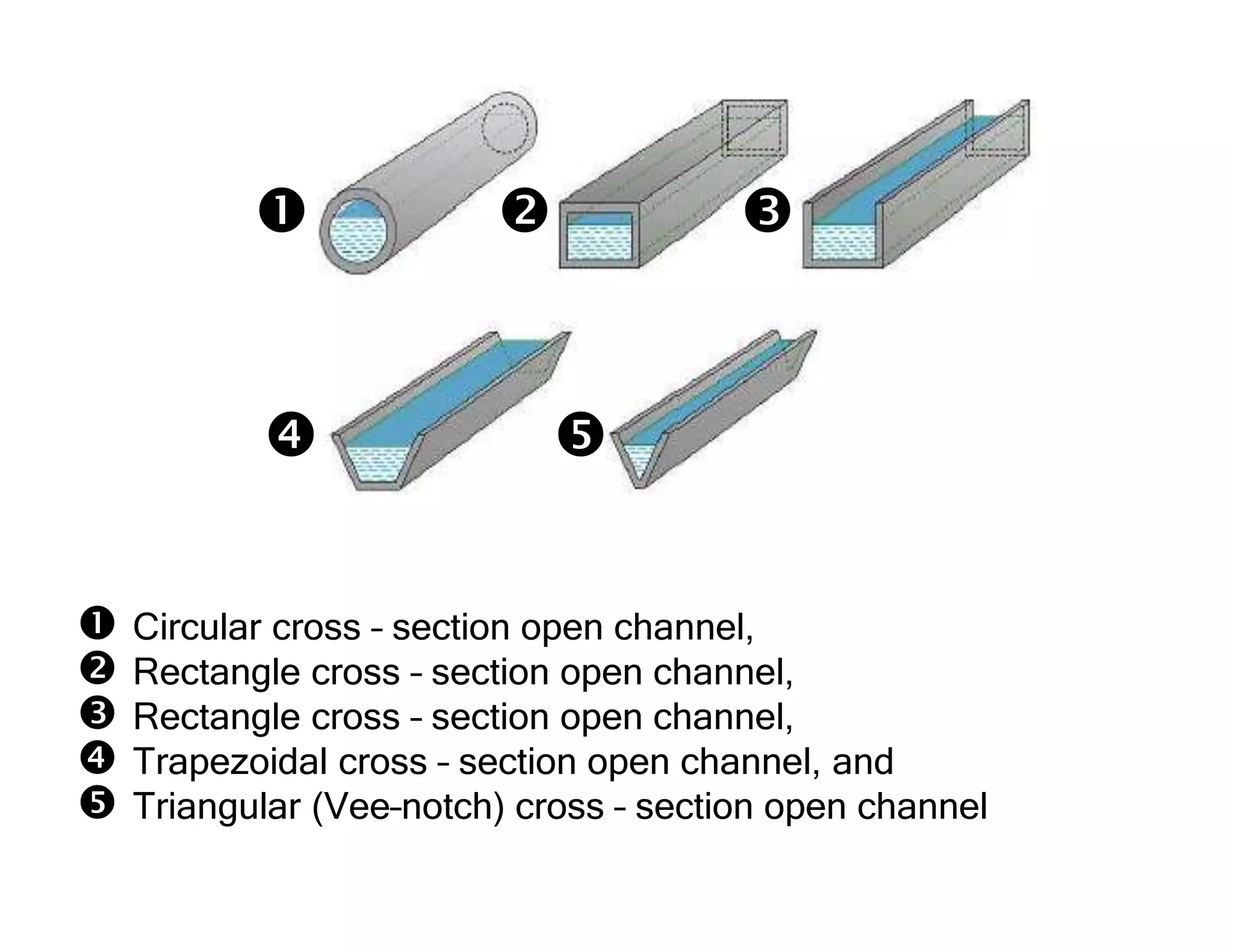
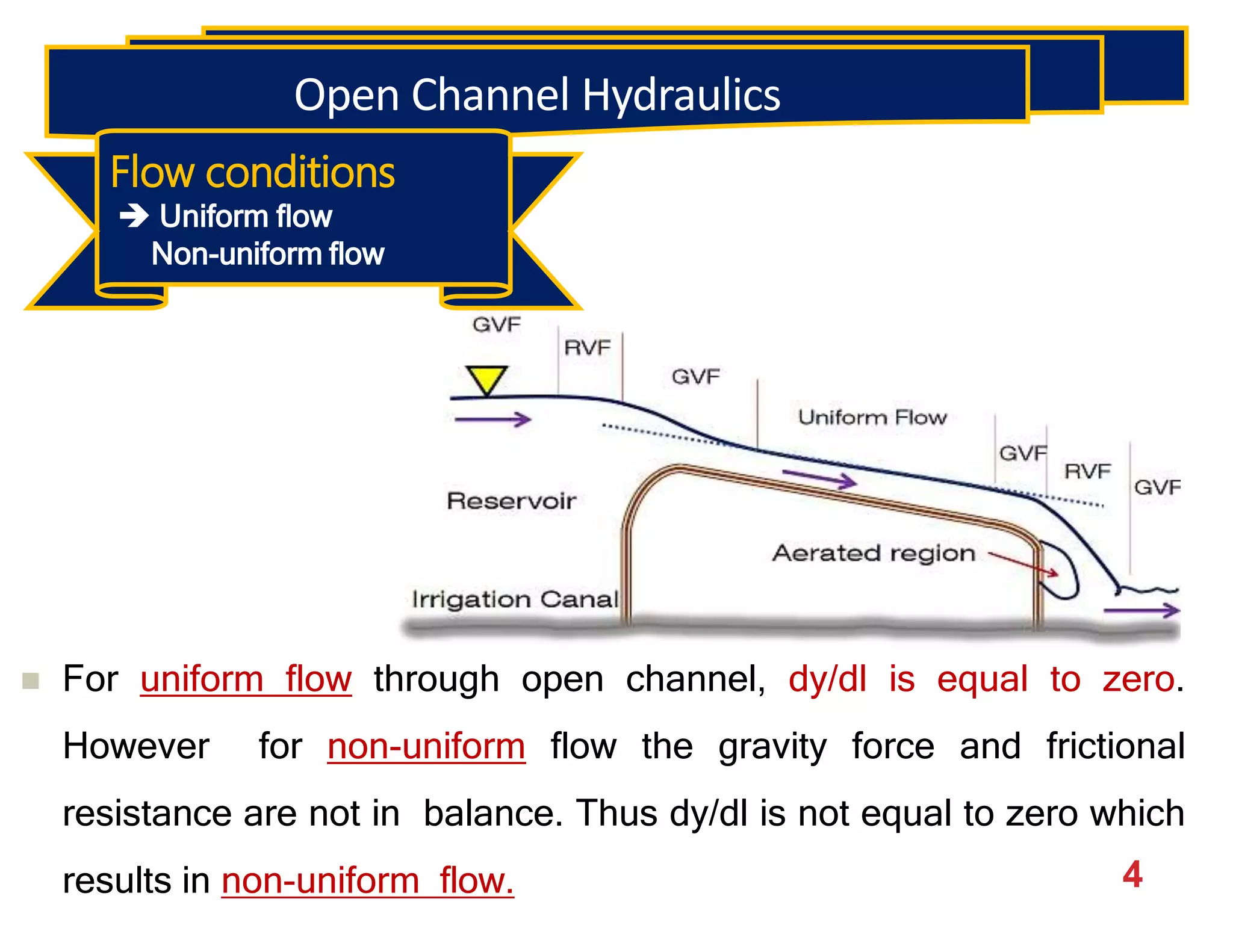
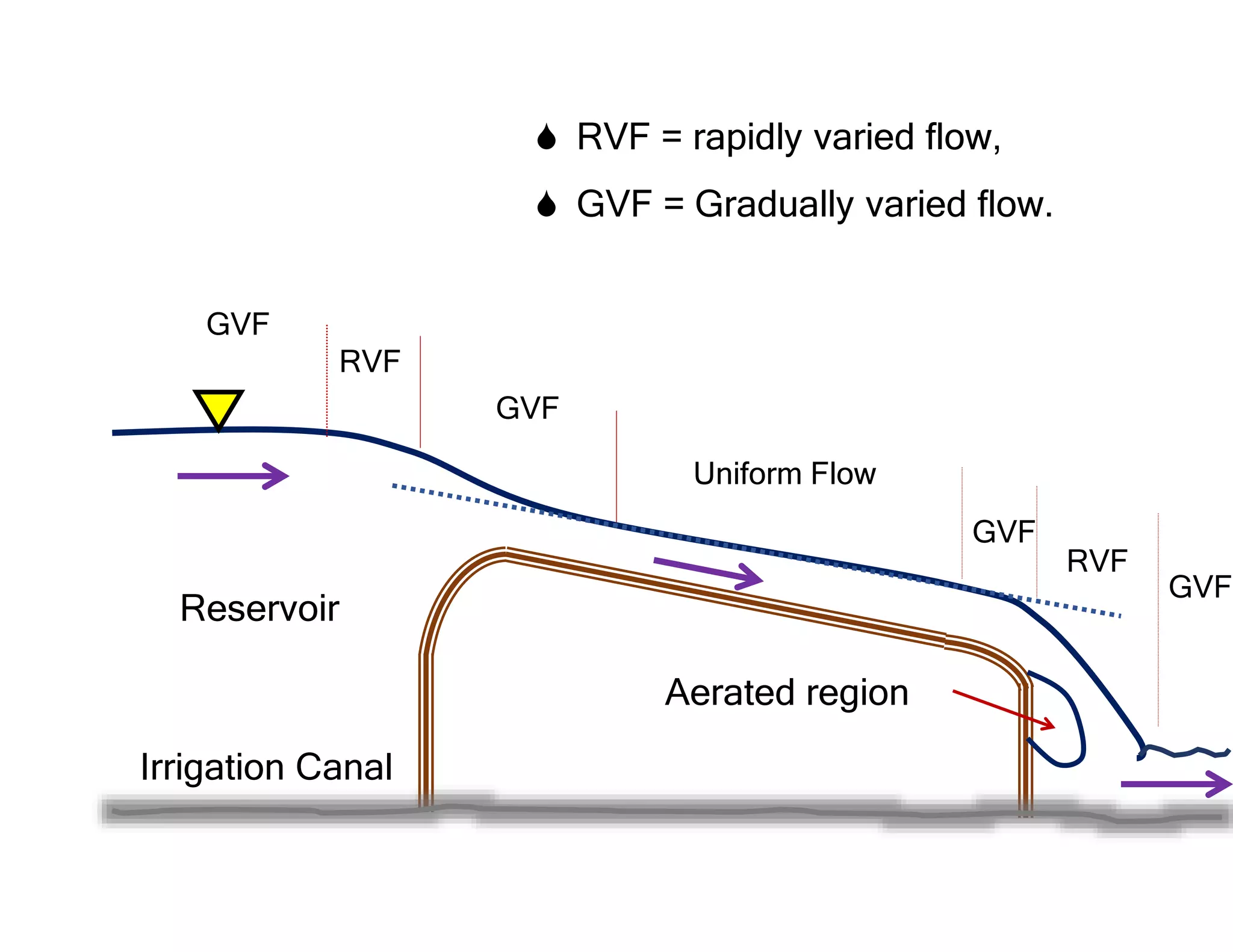
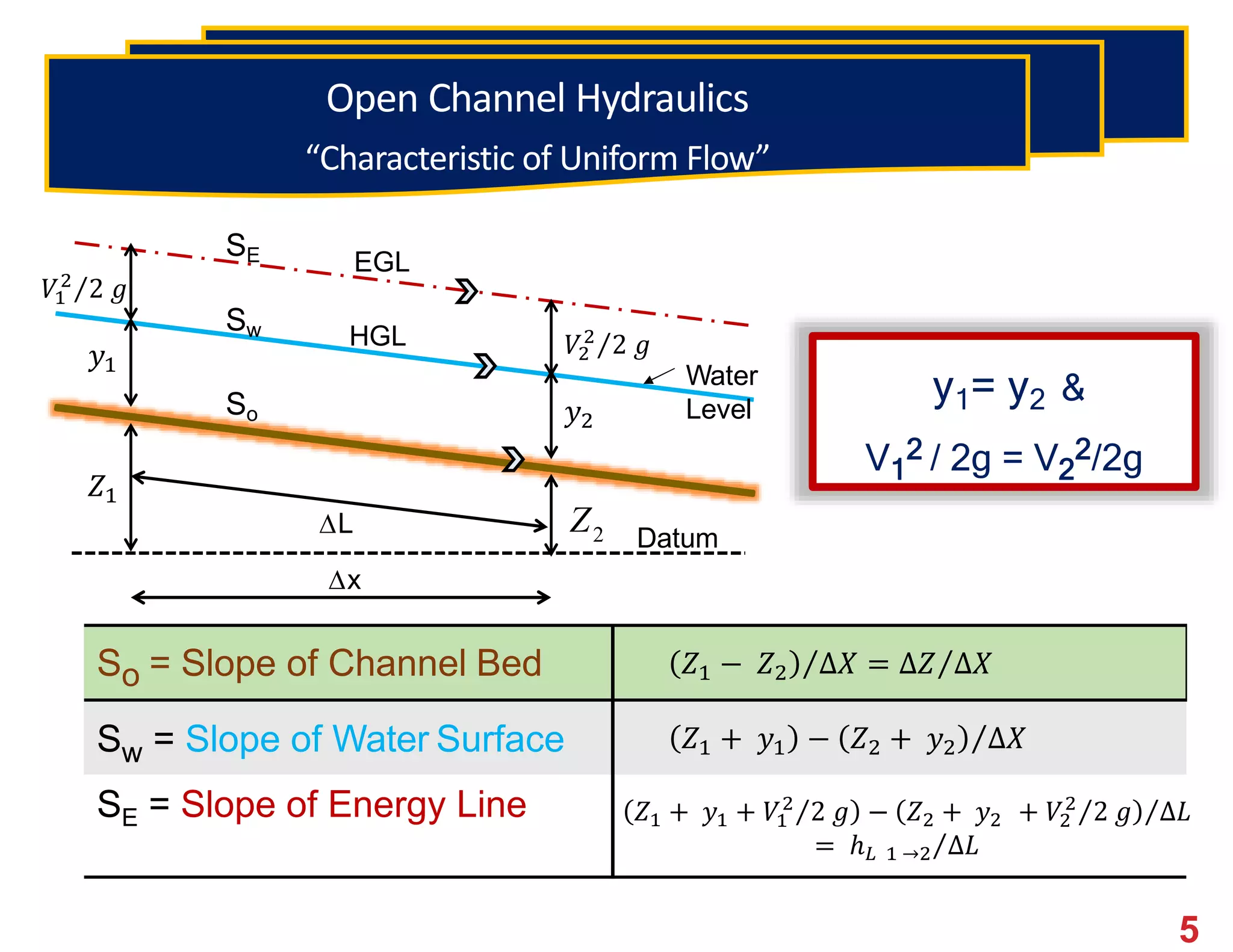
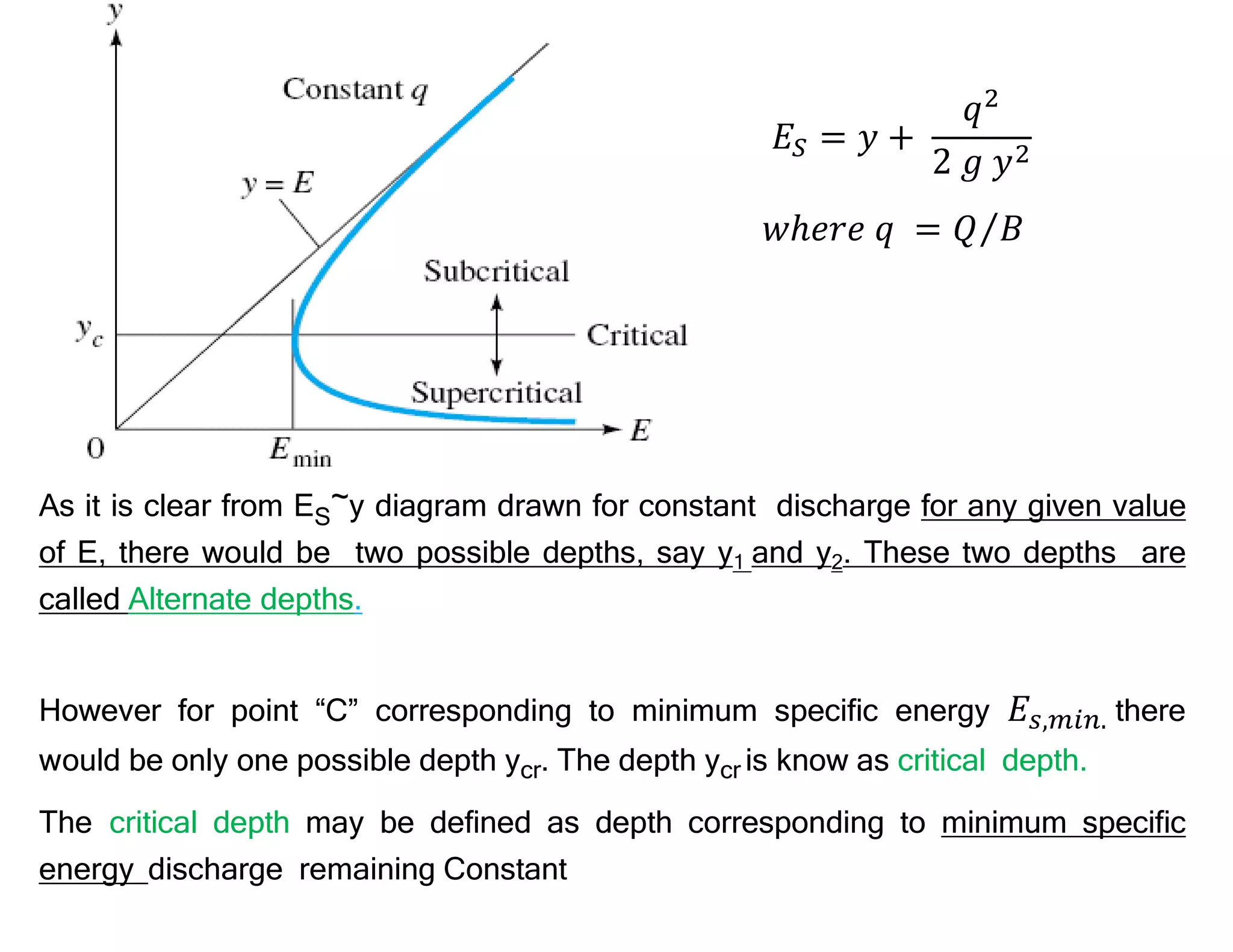
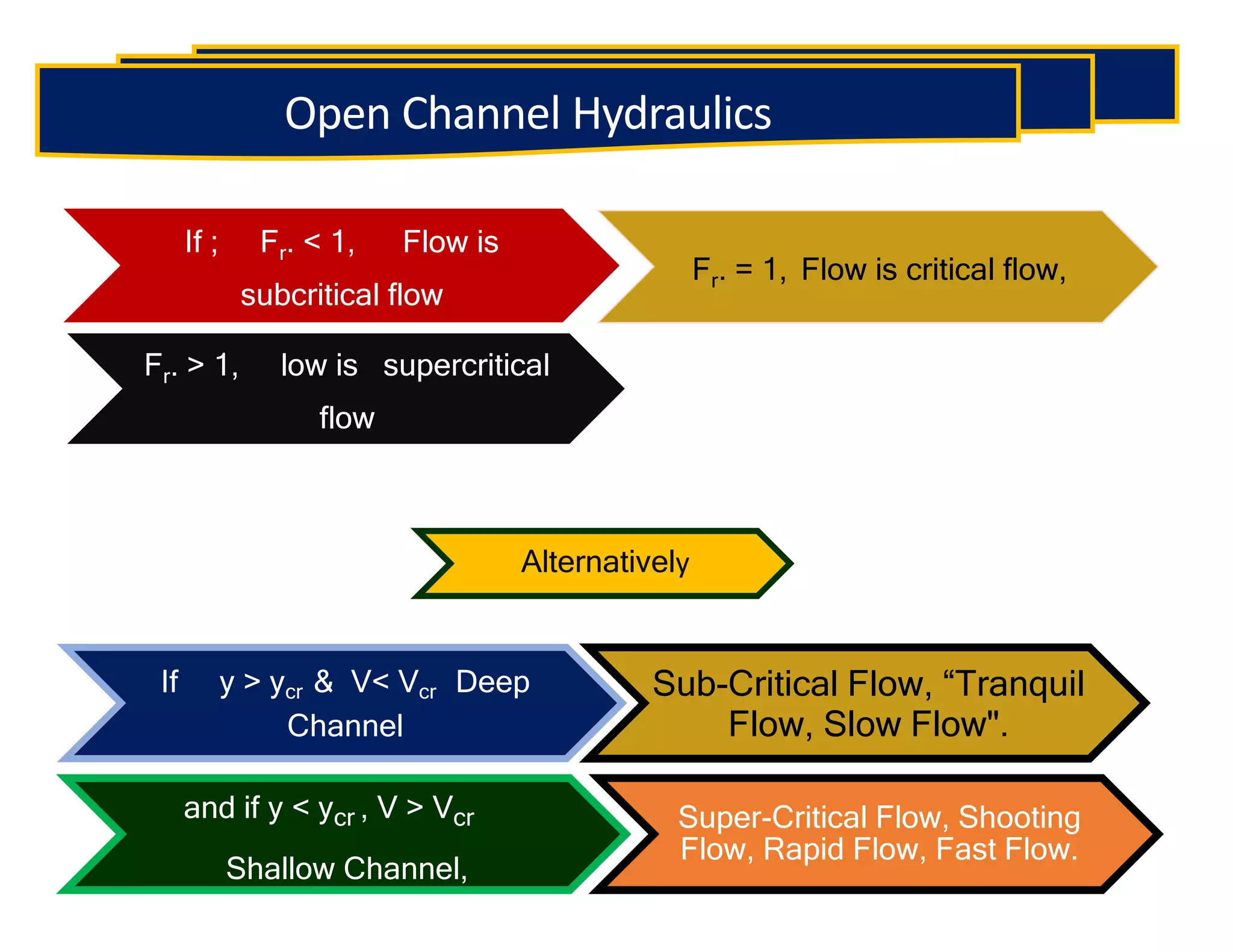
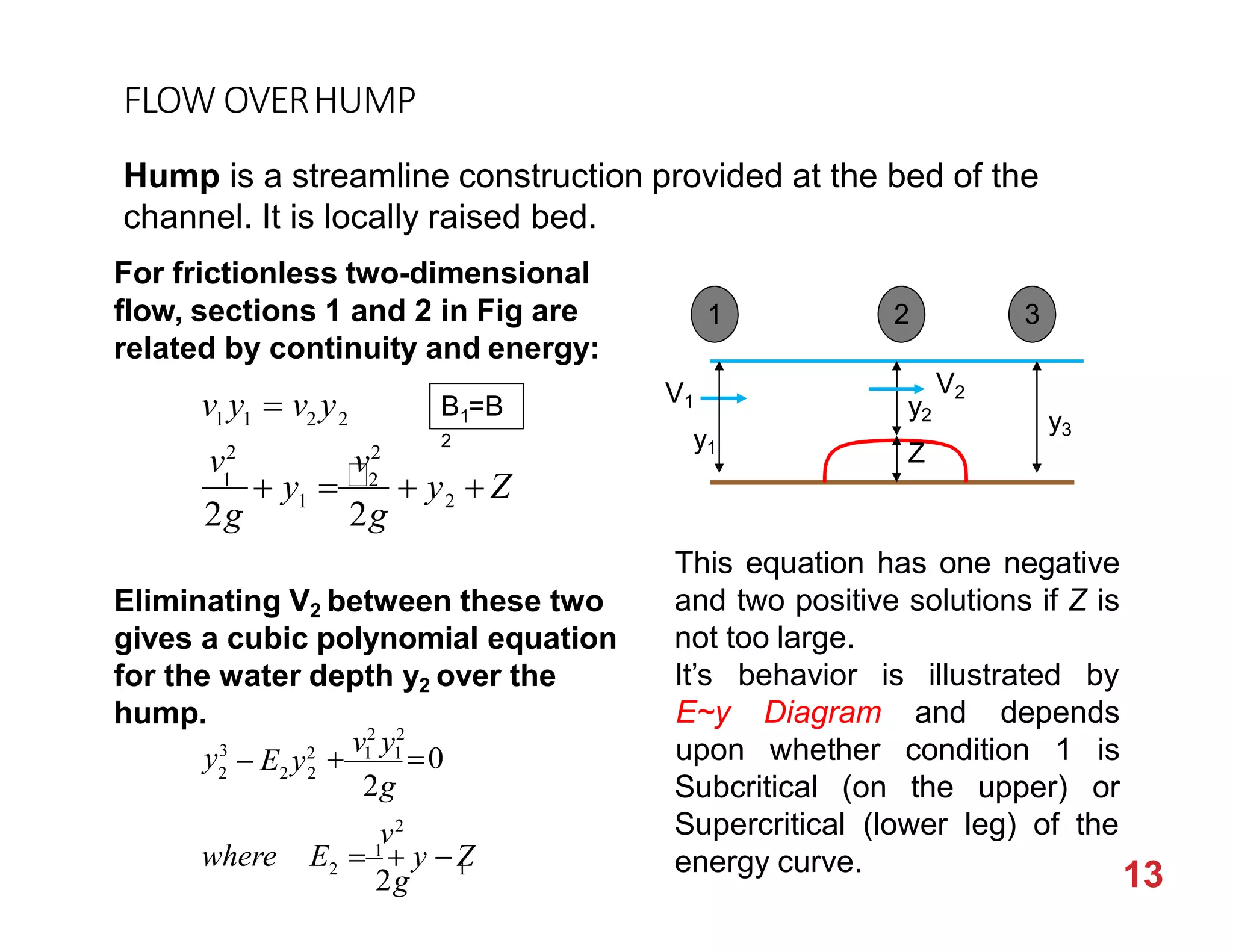
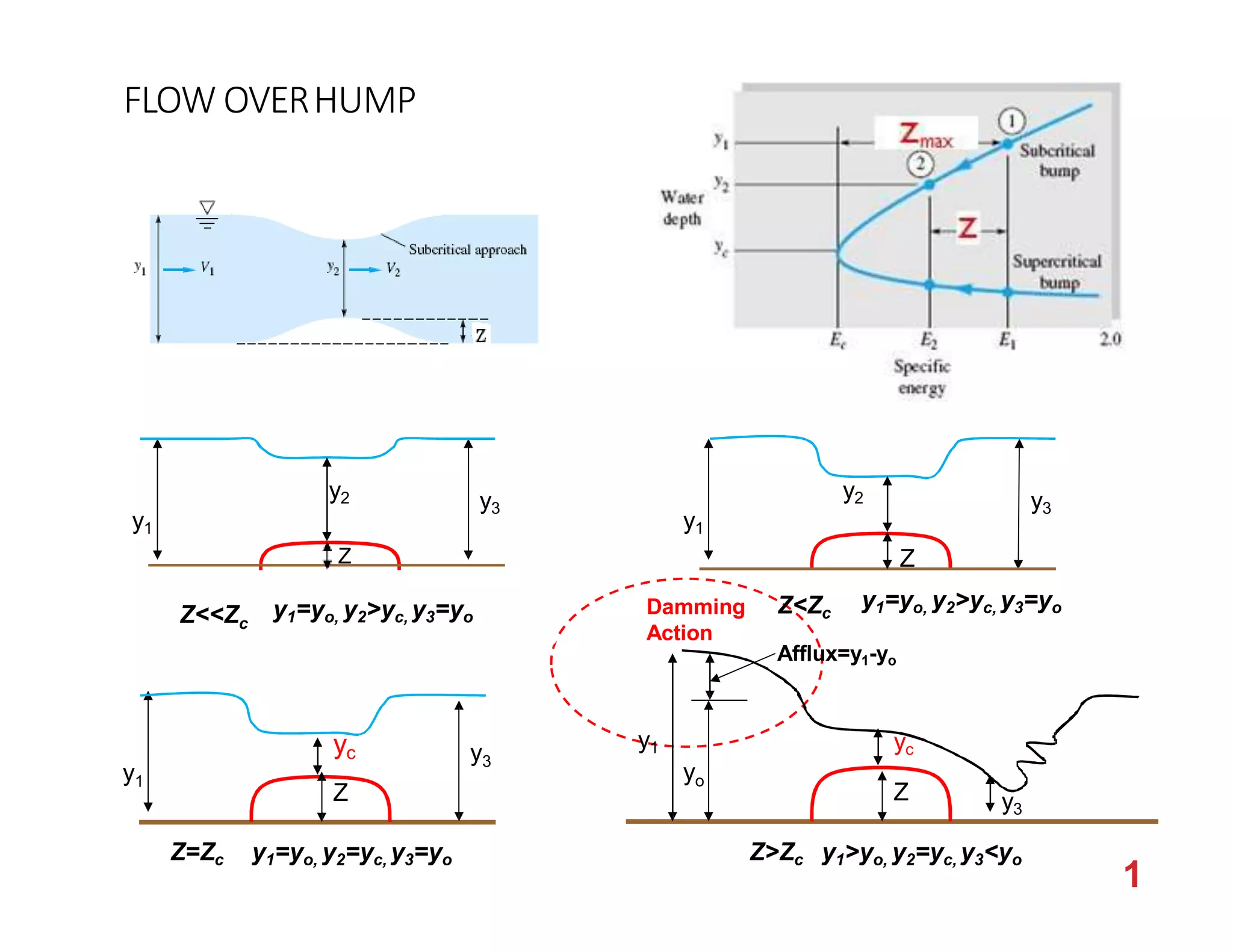
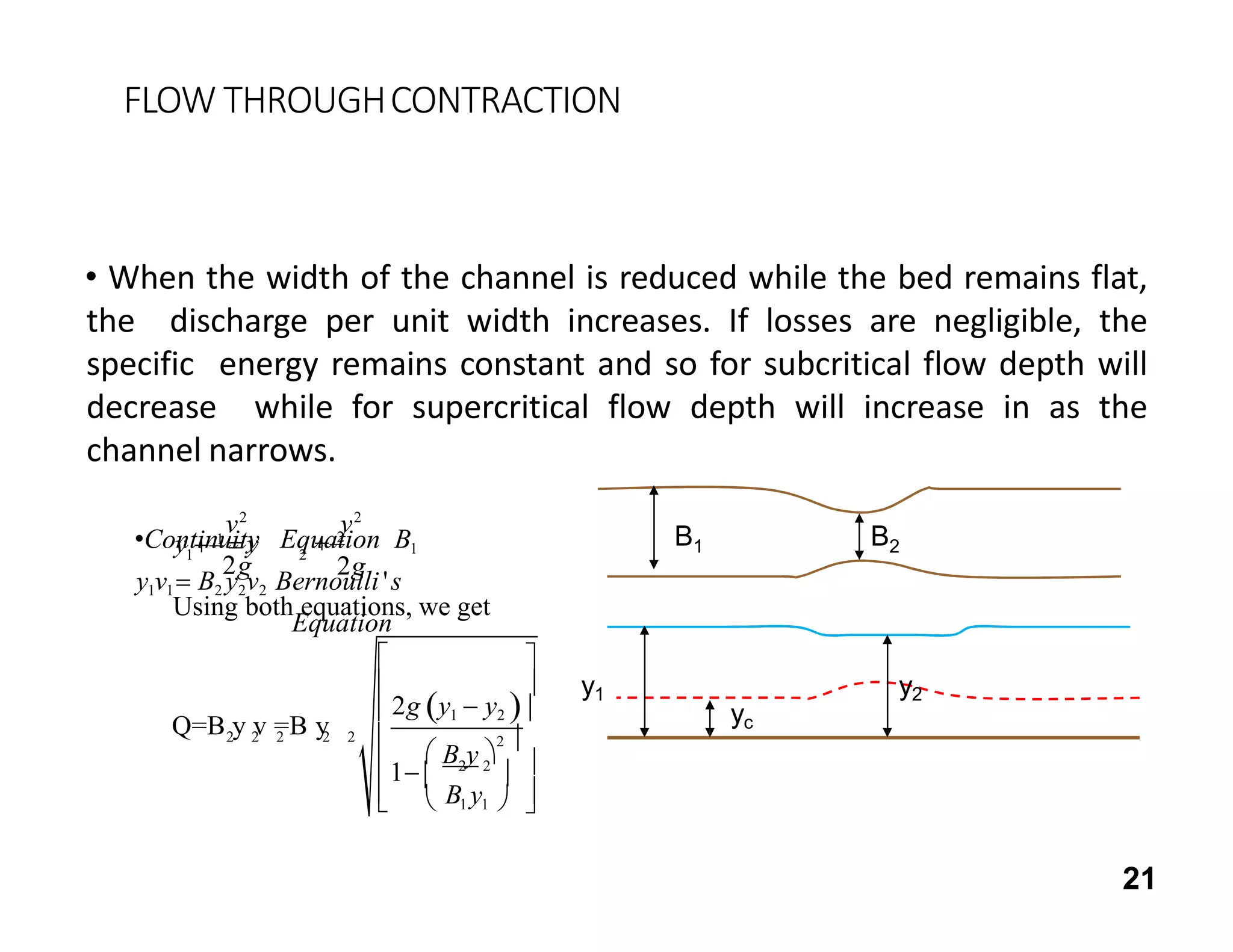
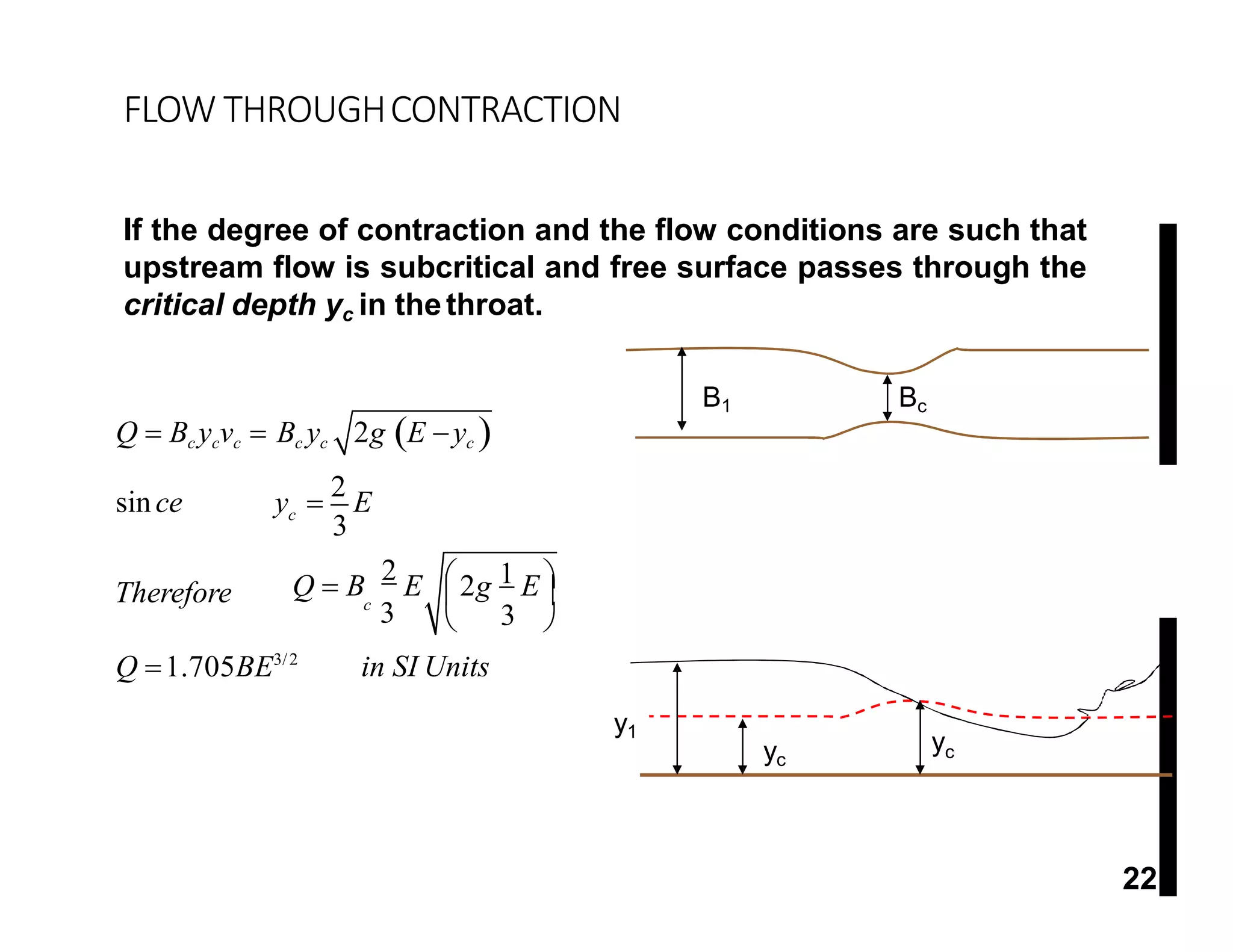
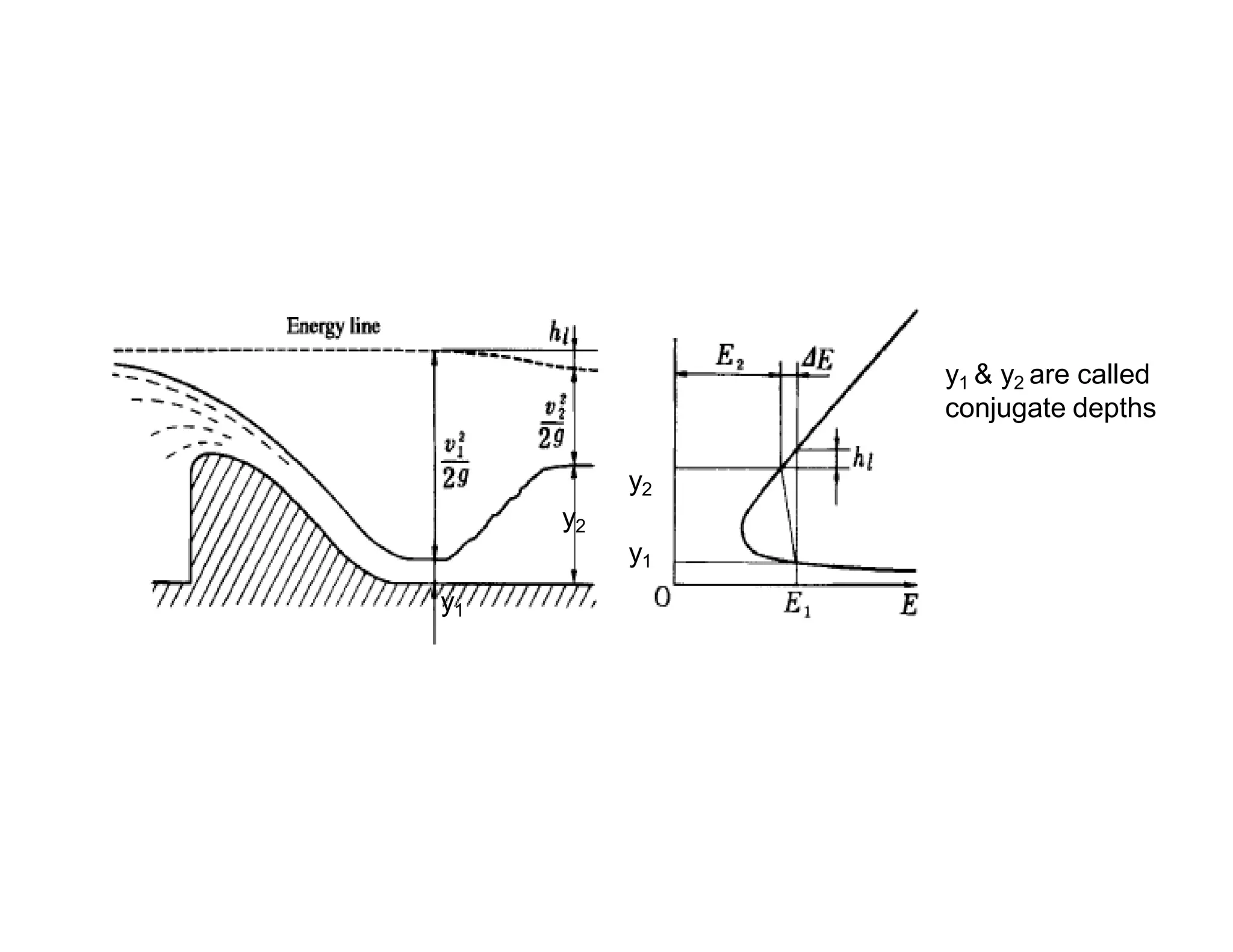
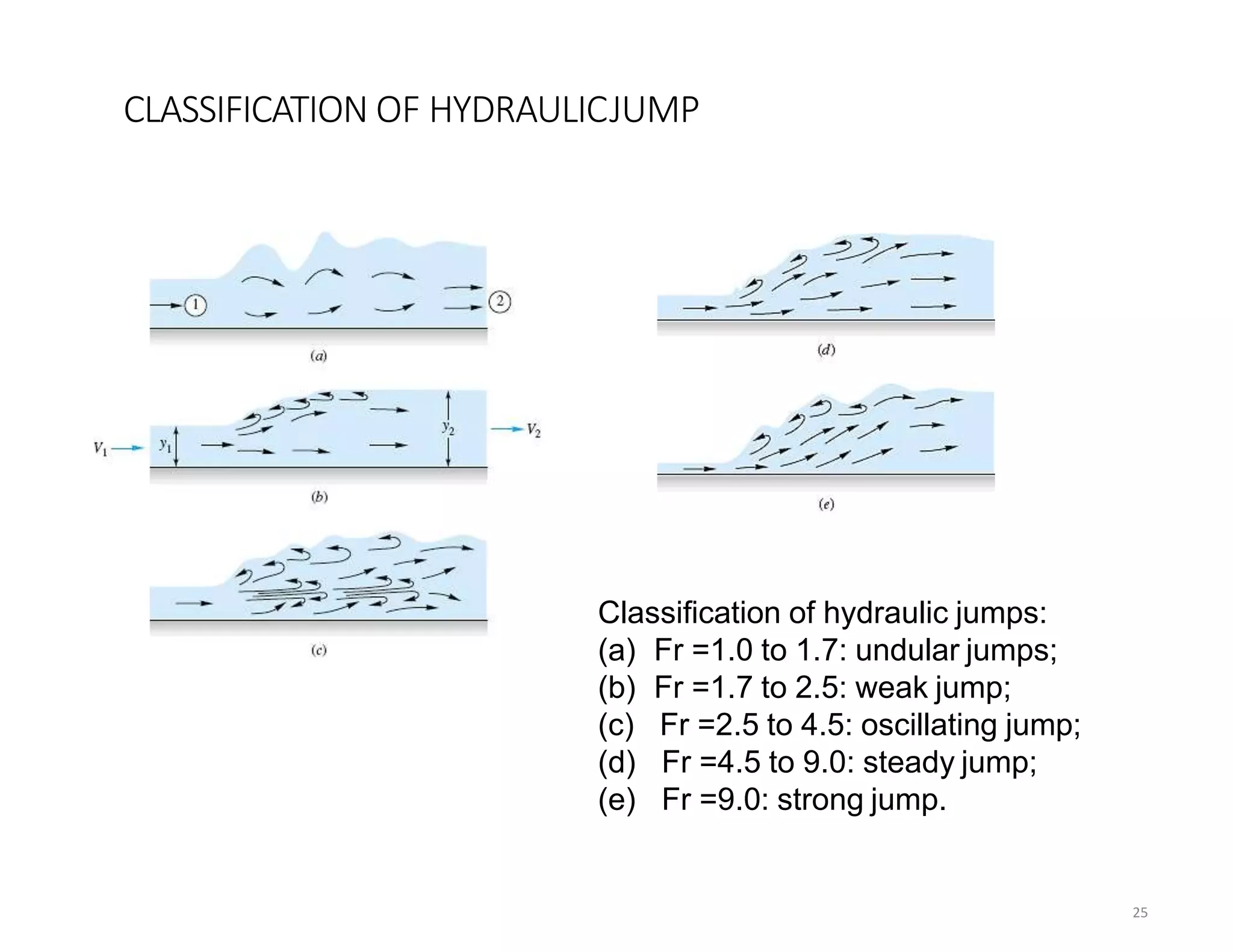
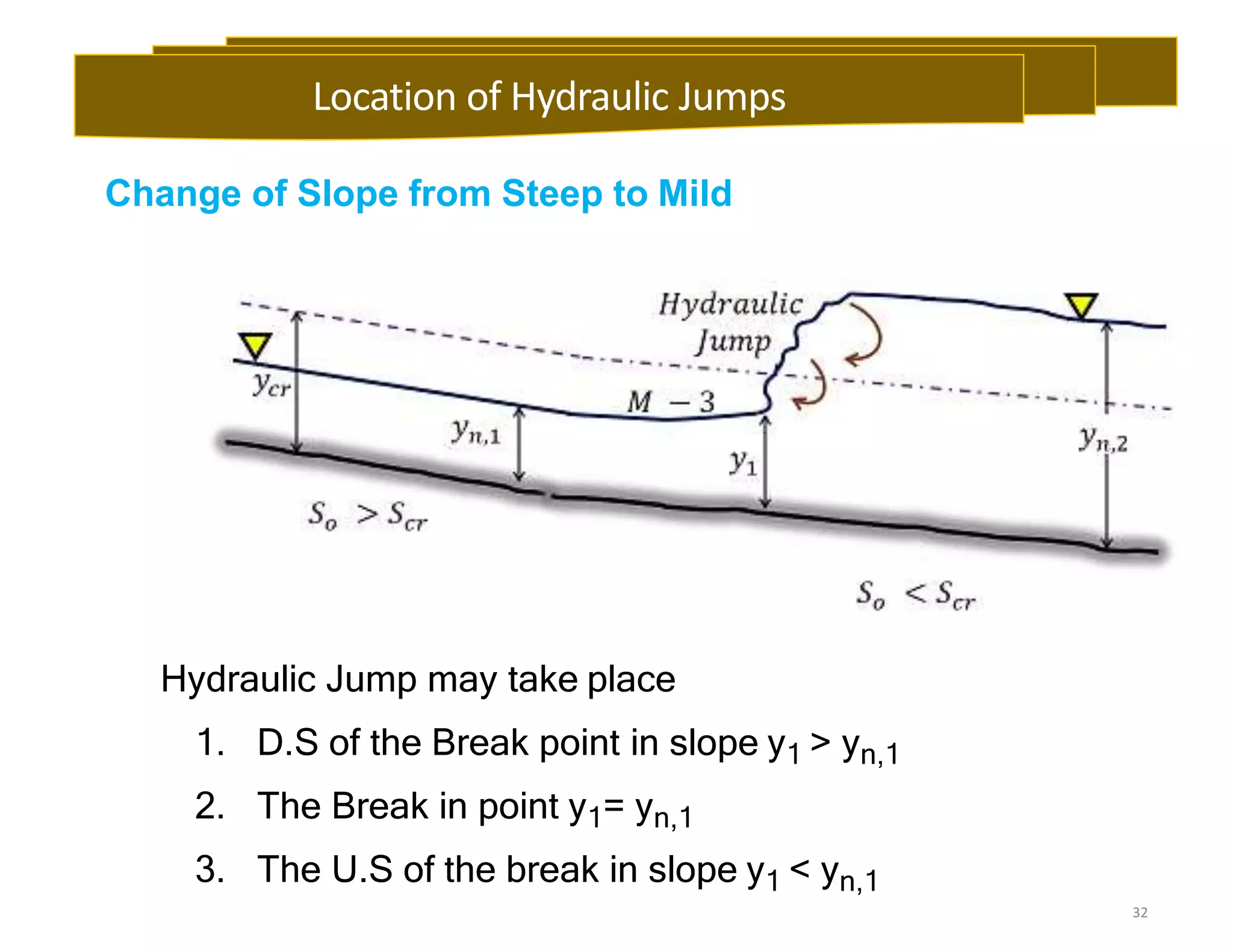
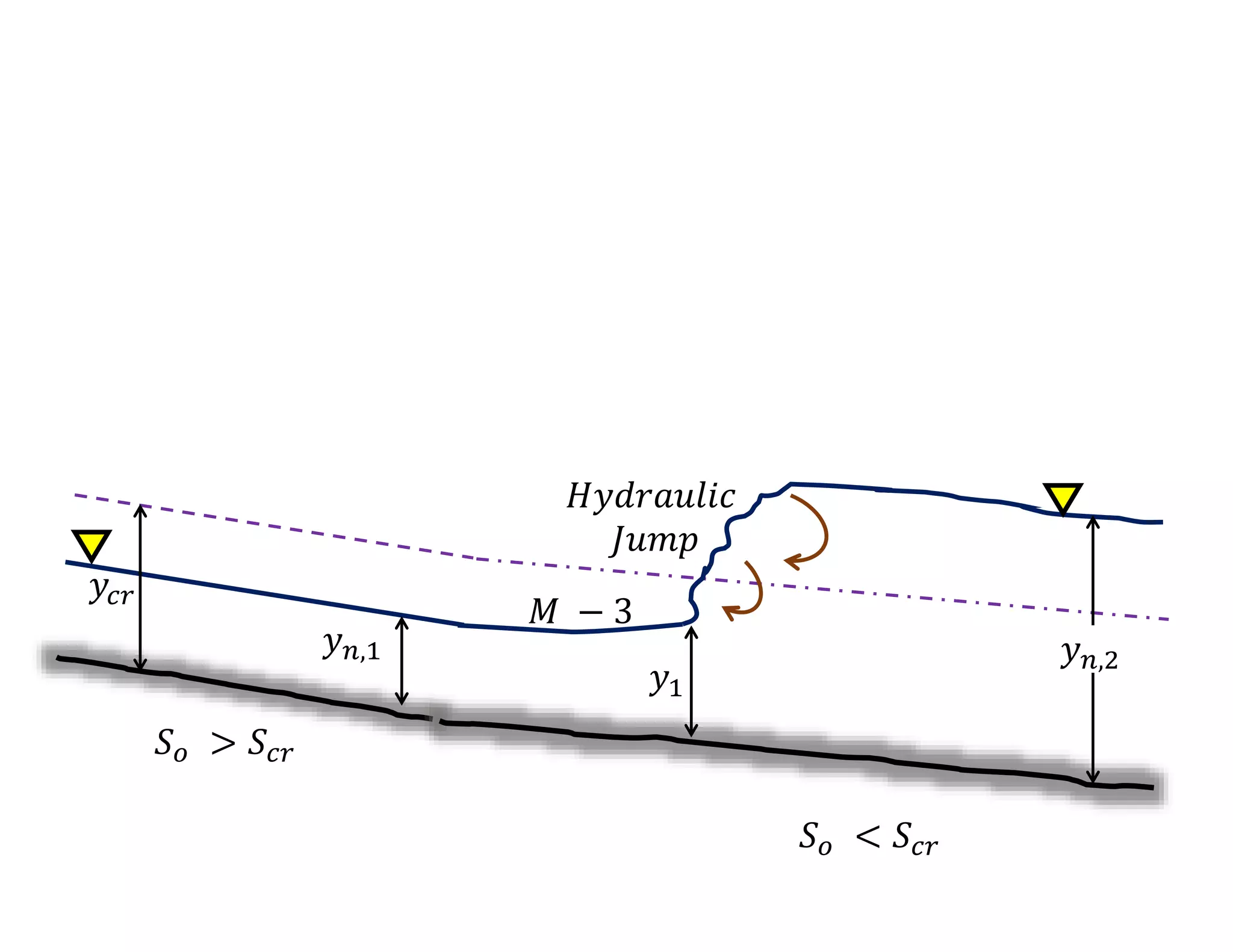
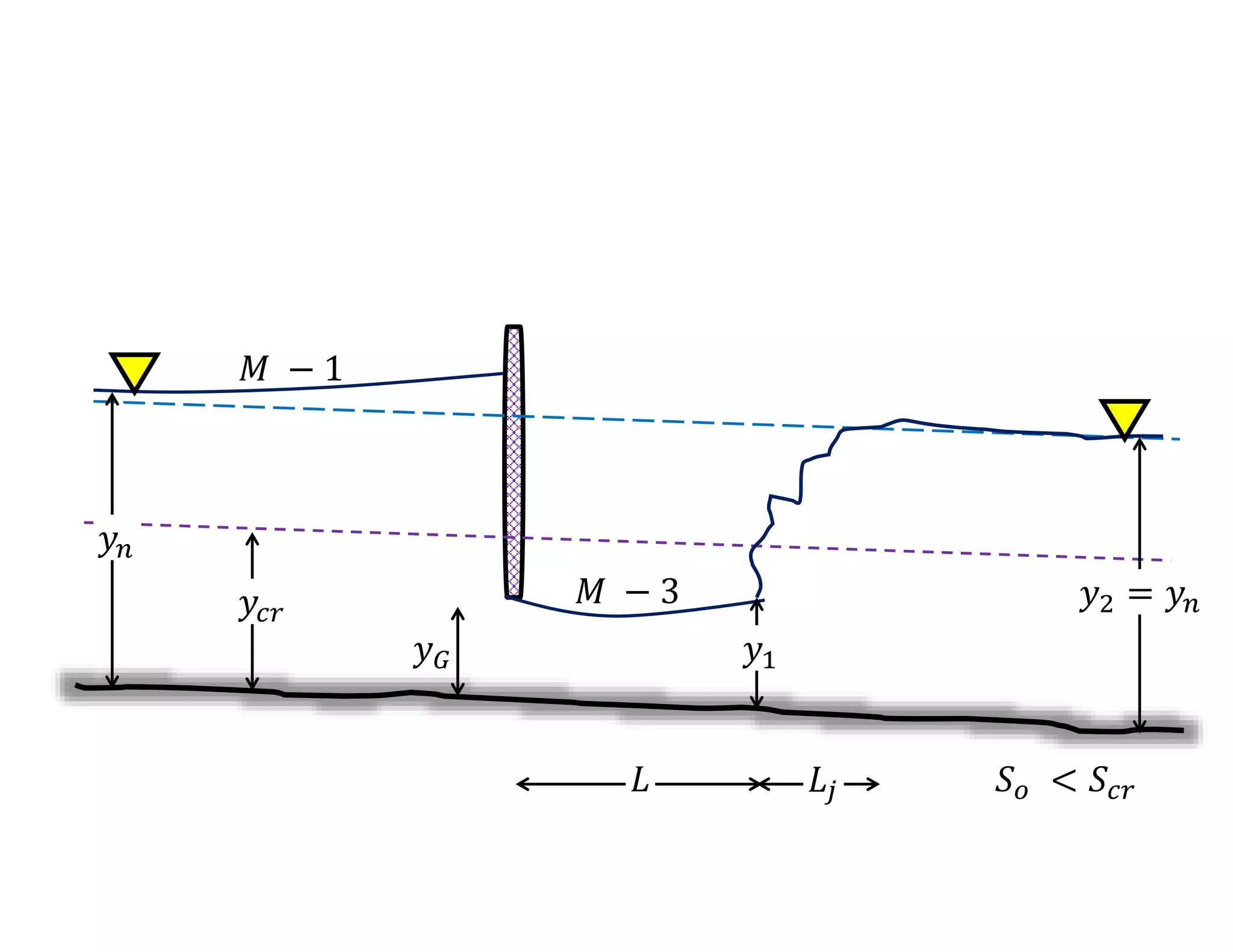
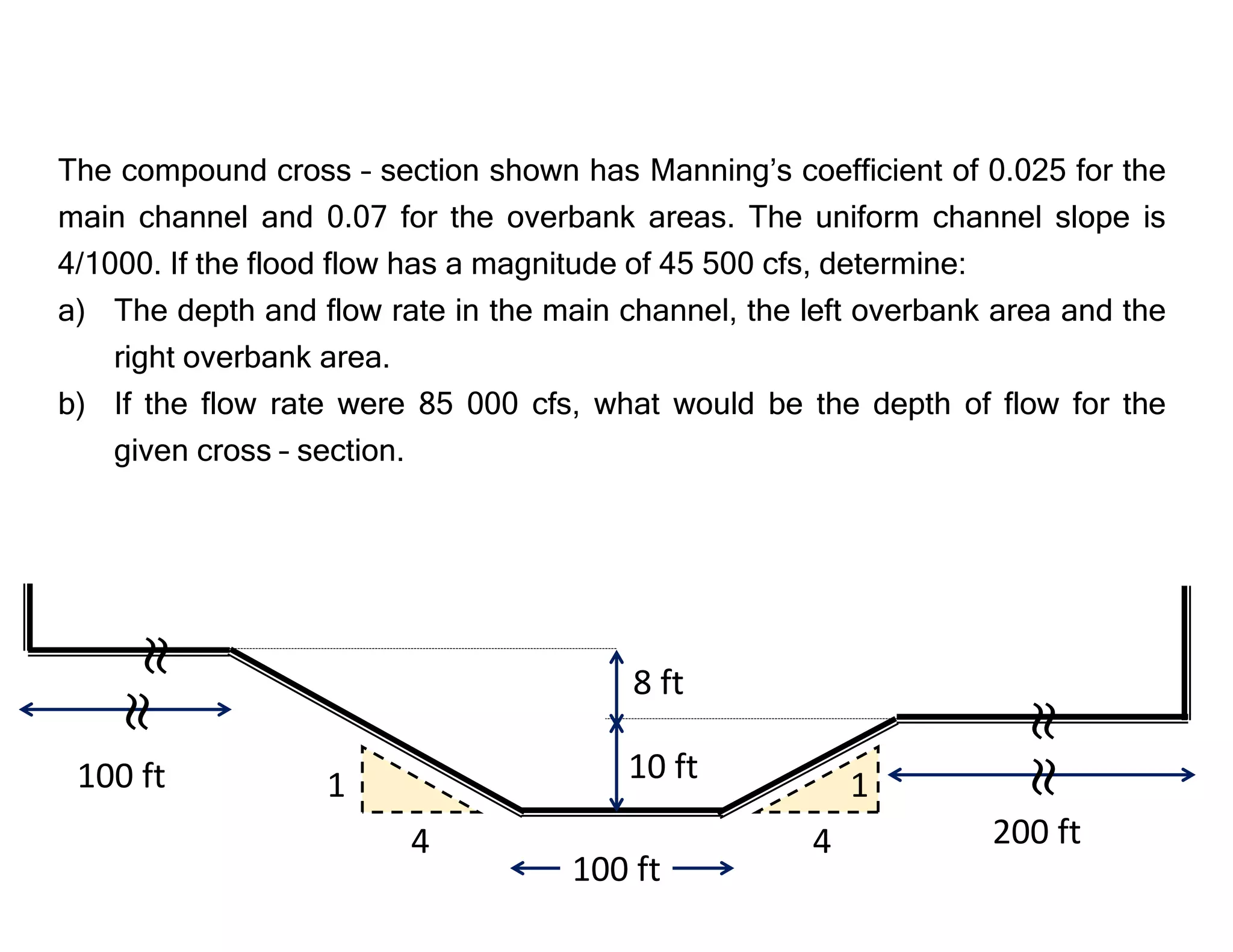
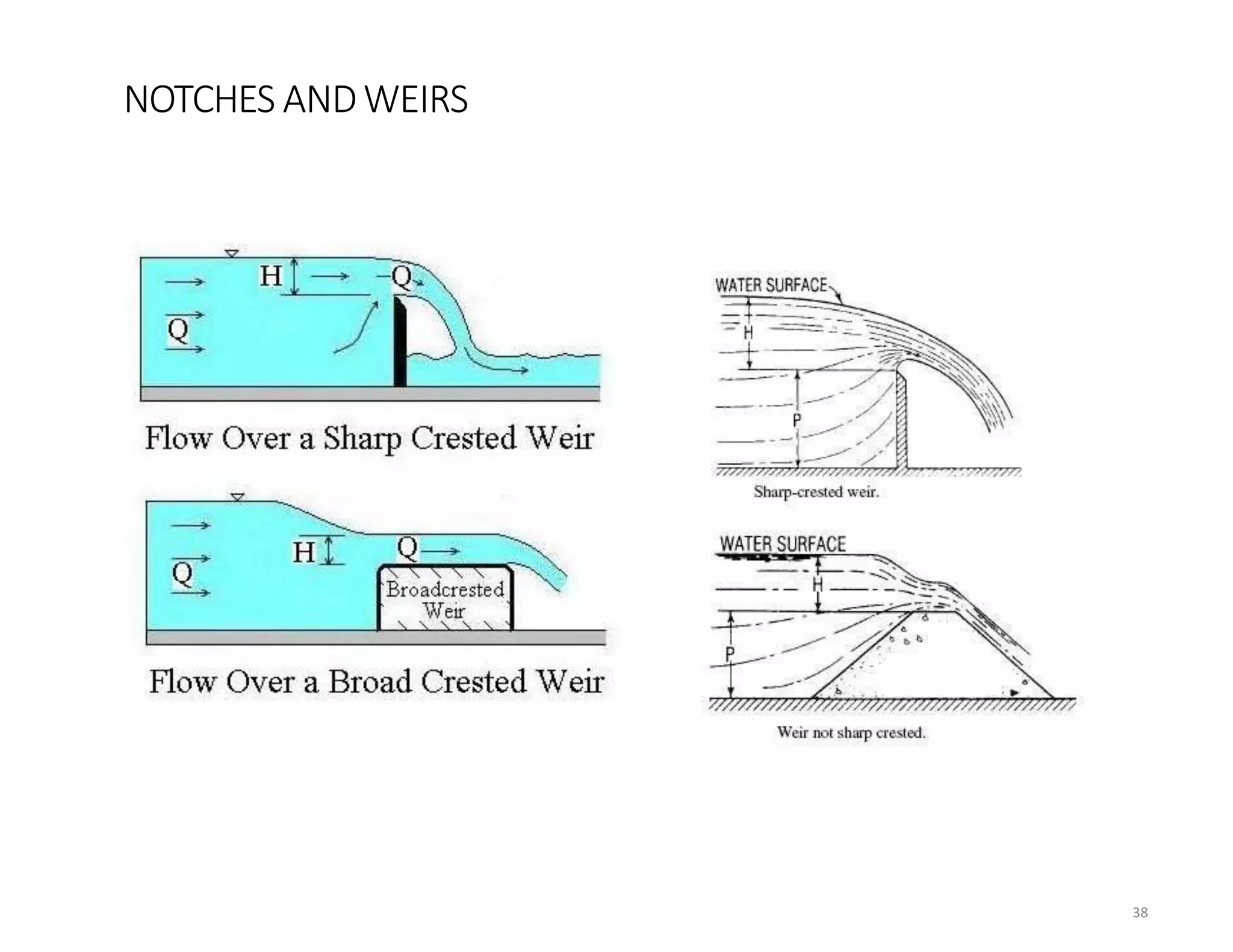
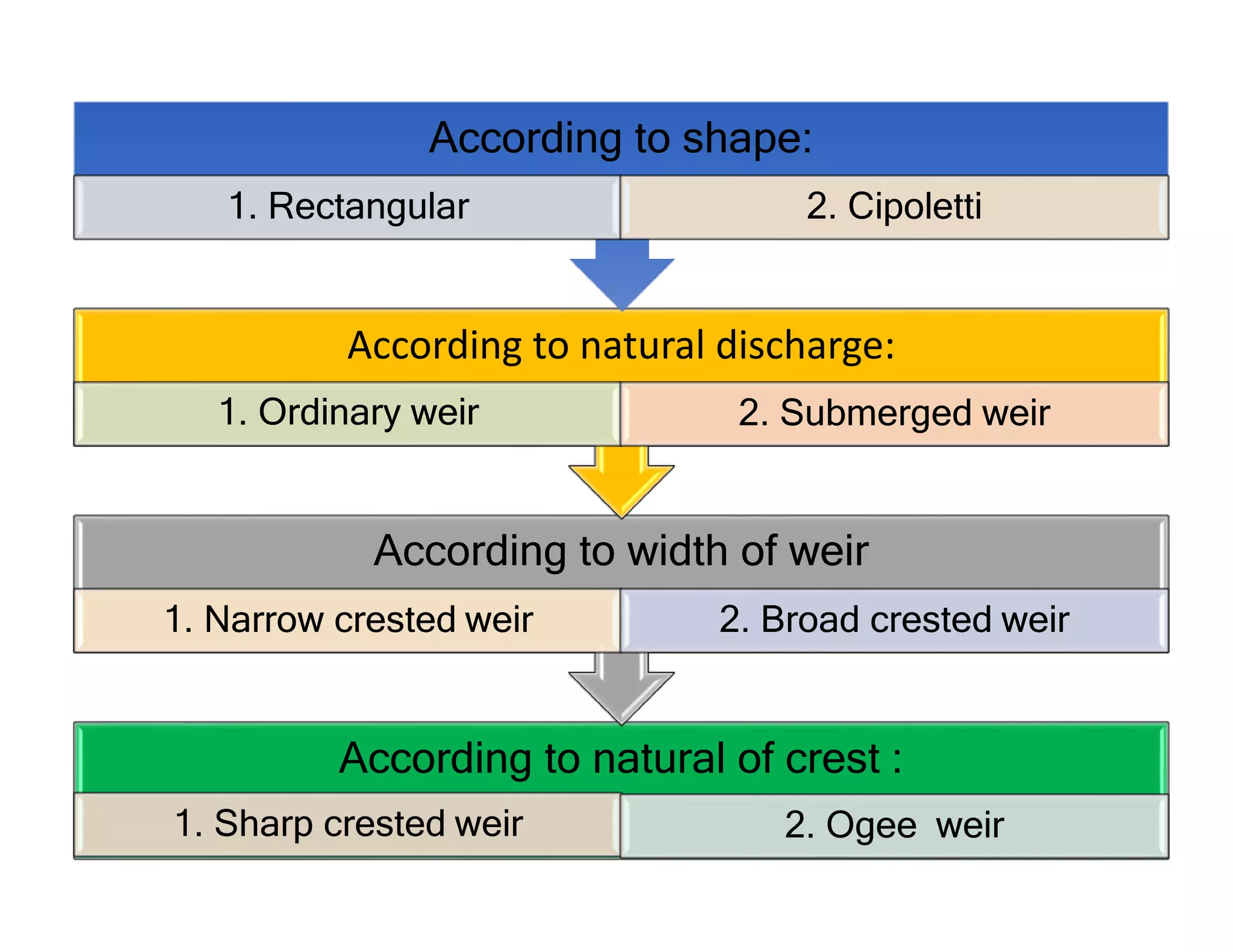
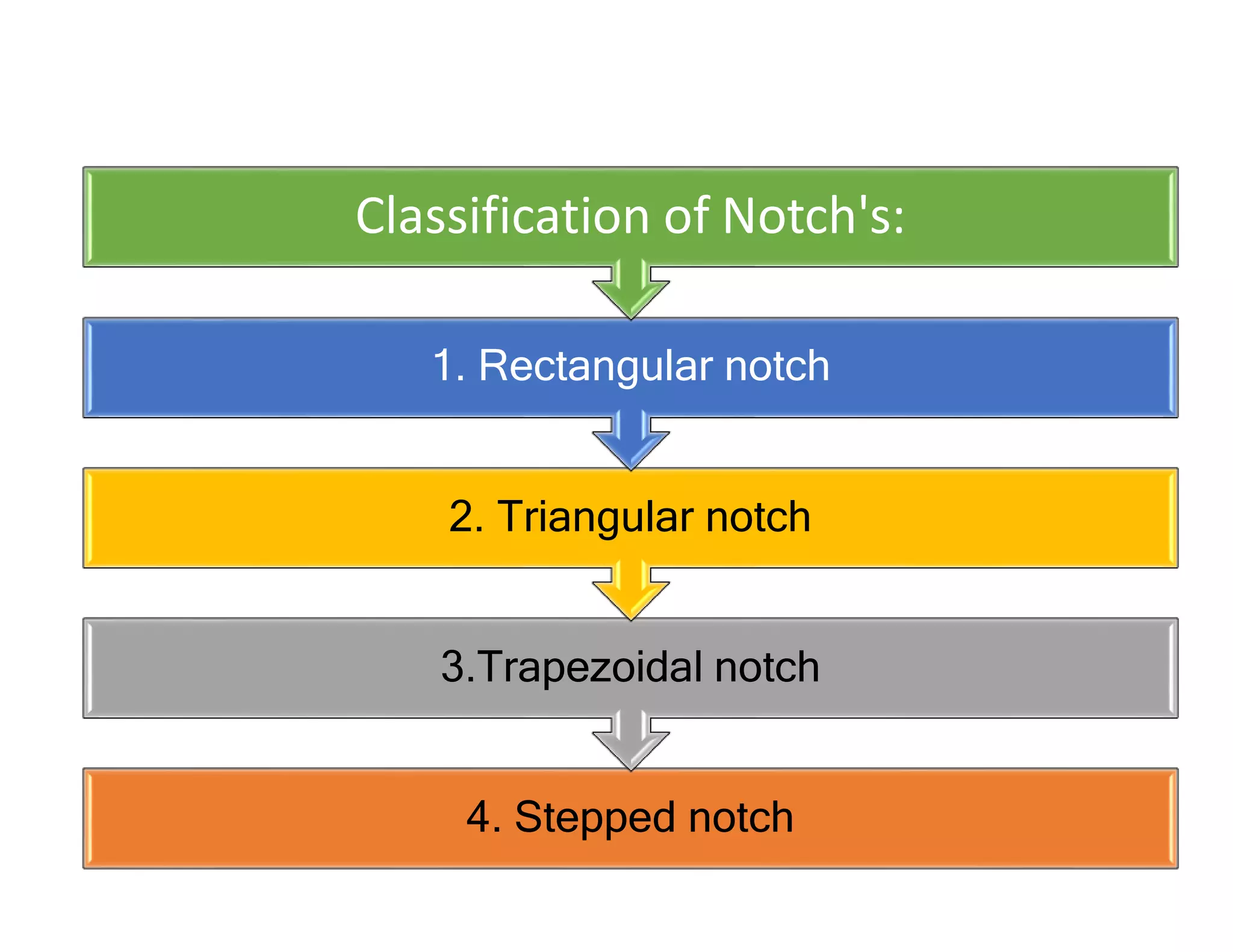
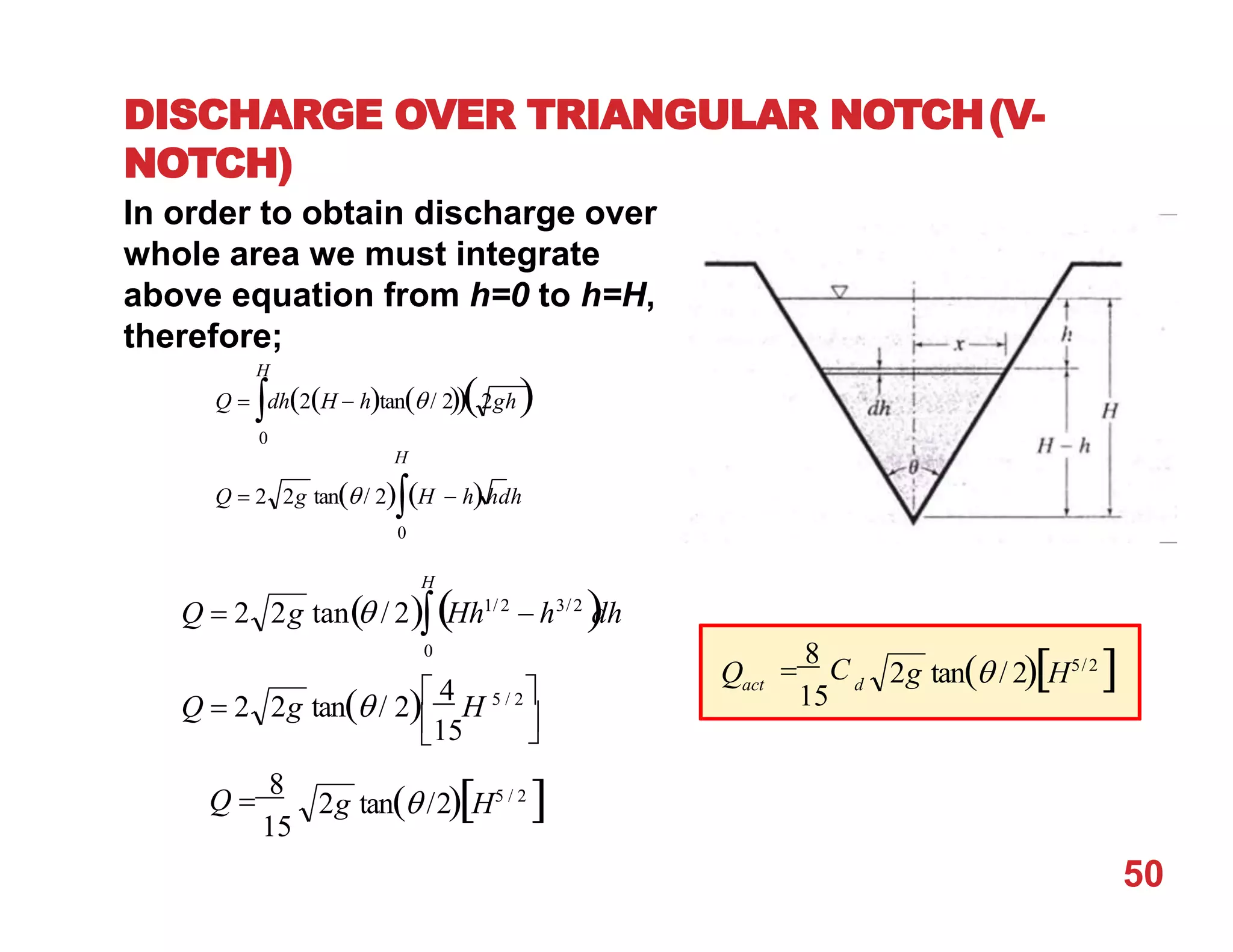
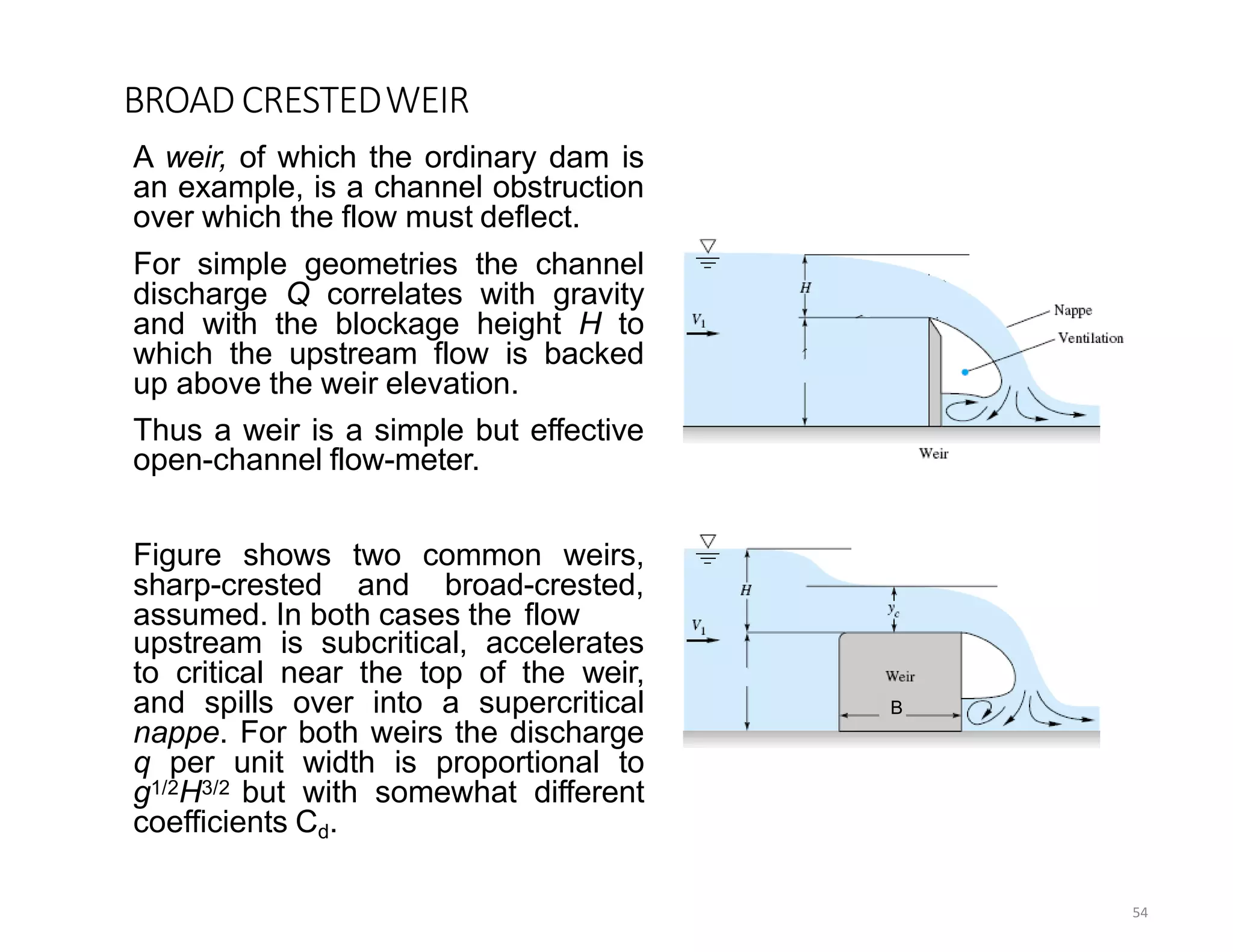
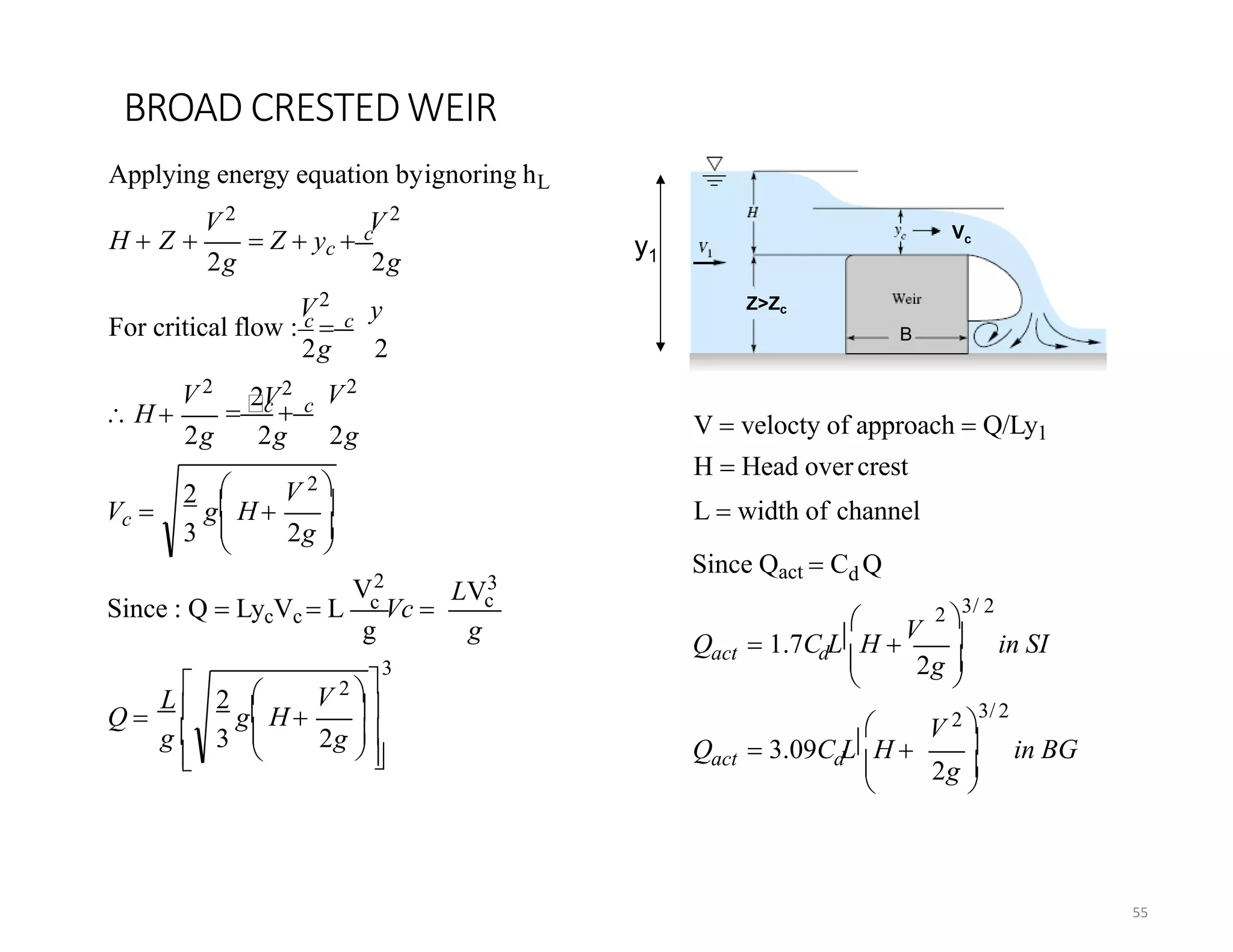
This document provides an overview of open channel hydraulics and discharge measuring structures. It discusses various open channel flow conditions including uniform flow, gradually varied flow, rapidly varied flow, subcritical flow, critical flow and supercritical flow. It introduces concepts such as specific energy, critical depth, energy equations, and hydraulic principles that govern open channel design. Formulas for discharge measurement using weirs and flumes are presented, such as the Chezy and Manning's equations. Common channel shapes and examples of flow through contractions and over humps are also summarized.