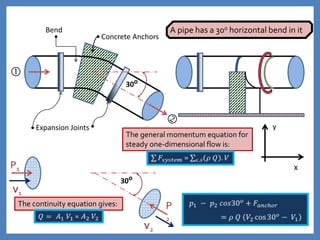
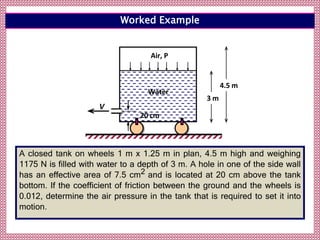
The document is a lecture on linear momentum and the linear momentum equation. It begins with definitions of linear momentum and Newton's second and third laws of motion. It then covers the conservation of momentum principle and introduces the general form of the linear momentum equation. Several examples of applying the linear momentum equation to problems involving pipes, nozzles, and hydraulic machines are shown. It also discusses the momentum correction factor and defines key aspects of using a control volume in the linear momentum equation.