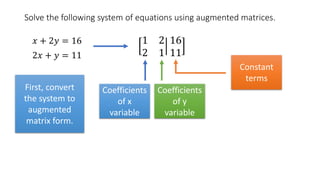
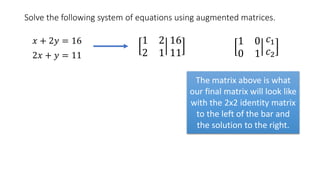
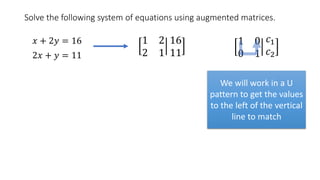
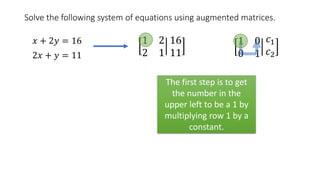
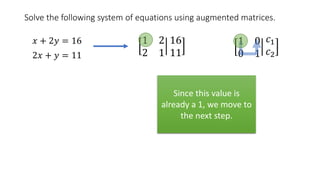
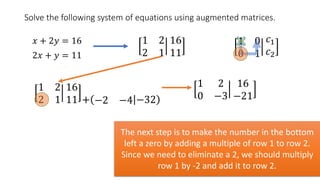
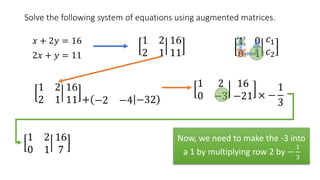
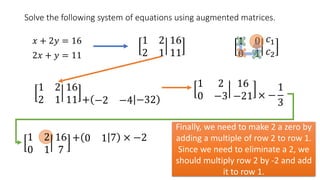
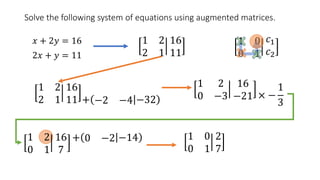
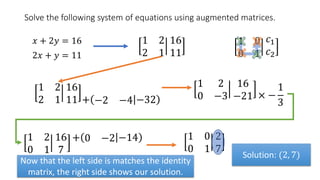
The document solves the system of equations x + 2y = 16 and 2x + y = 11 using augmented matrices. It first writes the system as an augmented matrix and then performs row operations, multiplying rows by constants and adding rows together, to transform the matrix into an identity matrix with the solutions in the right column. The solutions are x = 2 and y = 7.

1. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11

2. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
First, convert
the system to
augmented
matrix form.
1 2
2 1
16
11
Coefficients
of x
variable
Coefficients
of y
variable
Constant
terms

3. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
The matrix above is what
our final matrix will look like
with the 2x2 identity matrix
to the left of the bar and
the solution to the right.

4. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
We will work in a U
pattern to get the values
to the left of the vertical
line to match

5. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
The first step is to get
the number in the
upper left to be a 1 by
multiplying row 1 by a
constant.

6. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
Since this value is
already a 1, we move to
the next step.

7. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
The next step is to make the number in the bottom
left a zero by adding a multiple of row 1 to row 2.
Since we need to eliminate a 2, we should multiply
row 1 by -2 and add it to row 2.
1 2
2 1
16
11 + 1 2 16 × −2

8. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
The next step is to make the number in the bottom
left a zero by adding a multiple of row 1 to row 2.
Since we need to eliminate a 2, we should multiply
row 1 by -2 and add it to row 2.
1 2
2 1
16
11 + −2 −4 −32
1 2
0 −3
16
−21

9. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
Now, we need to make the -3 into
a 1 by multiplying row 2 by −
1
3
1 2
2 1
16
11 + −2 −4 −32
1 2
0 −3
16
−21 × −
1
3
1 2
0 1
16
7

10. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
1 2
2 1
16
11 + −2 −4 −32
1 2
0 −3
16
−21 × −
1
3
1 2
0 1
16
7
Finally, we need to make 2 a zero by
adding a multiple of row 2 to row 1.
Since we need to eliminate a 2, we
should multiply row 2 by -2 and add
it to row 1.
+ 0 1 7 × −2

11. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
1 2
2 1
16
11 + −2 −4 −32
1 2
0 −3
16
−21 × −
1
3
1 2
0 1
16
7
+ 0 −2 −14 1 0
0 1
2
7

12. Solve the following system of equations using augmented matrices.
𝑥 + 2𝑦 = 16
2𝑥 + 𝑦 = 11
1 2
2 1
16
11
1 0
0 1
𝑐1
𝑐2
1 2
2 1
16
11 + −2 −4 −32
1 2
0 −3
16
−21 × −
1
3
1 2
0 1
16
7
+ 0 −2 −14 1 0
0 1
2
7
Now that the left side is matches the identity
matrix, the right side shows our solution.
Solution: (2, 7)