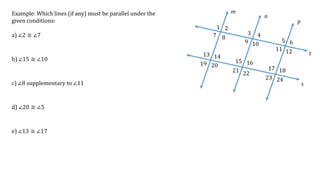
The document analyzes five conditions to determine which lines are parallel: a) No lines are parallel as ∠2 and ∠7 are vertical angles. b) Lines t and s are parallel as ∠15 and ∠10 are congruent alternate interior angles. c) Lines m and p are parallel as ∠8 and ∠11 are supplementary interior angles. d) No lines are parallel as four lines are needed to form the angles. e) Lines m and p are parallel as ∠13 and ∠17 are congruent corresponding angles.

1. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
b) ∠15 ≅ ∠10
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

2. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
b) ∠15 ≅ ∠10
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

3. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

4. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

5. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

6. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

7. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

8. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

9. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

10. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

11. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

12. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
We need four lines to form these angles.
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

13. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
We need four lines to form these angles.
Therefore, no lines are parallel.
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

14. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
We need four lines to form these angles.
Therefore, no lines are parallel.
e) ∠13 ≅ ∠17
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

15. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
We need four lines to form these angles.
Therefore, no lines are parallel.
e) ∠13 ≅ ∠17
Lines m and p with transversal s form these angles.
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s

16. 1 2
3 4
5 6
7 8
m
n
t
Example: Which lines (if any) must be parallel under the
given conditions:
a) ∠2 ≅ ∠7
We can see only two lines are needed to form these angles
∠2 and ∠7 are vertical angles which are always congruent,
therefore no lines are parallel
b) ∠15 ≅ ∠10
Lines t and s with transversal t form these angles.
∠15 and ∠10 are congruent alternate interior angles
Therefore, lines t and s are parallel.
c) ∠8 supplementary to ∠11
Lines m and p with transversal t form these angles.
∠8 and ∠11 are interior angles on the same side of the transversal
and are supplementary, therefore lines m and p are parallel.
d) ∠20 ≅ ∠5
We need four lines to form these angles.
Therefore, no lines are parallel.
e) ∠13 ≅ ∠17
Lines m and p with transversal s form these angles.
∠13 and ∠17 are congruent corresponding angles
Therefore, lines m and p are parallel.
9 10
11 1213 14
15 16
17 18
19 20
21 22
23 24
p
s