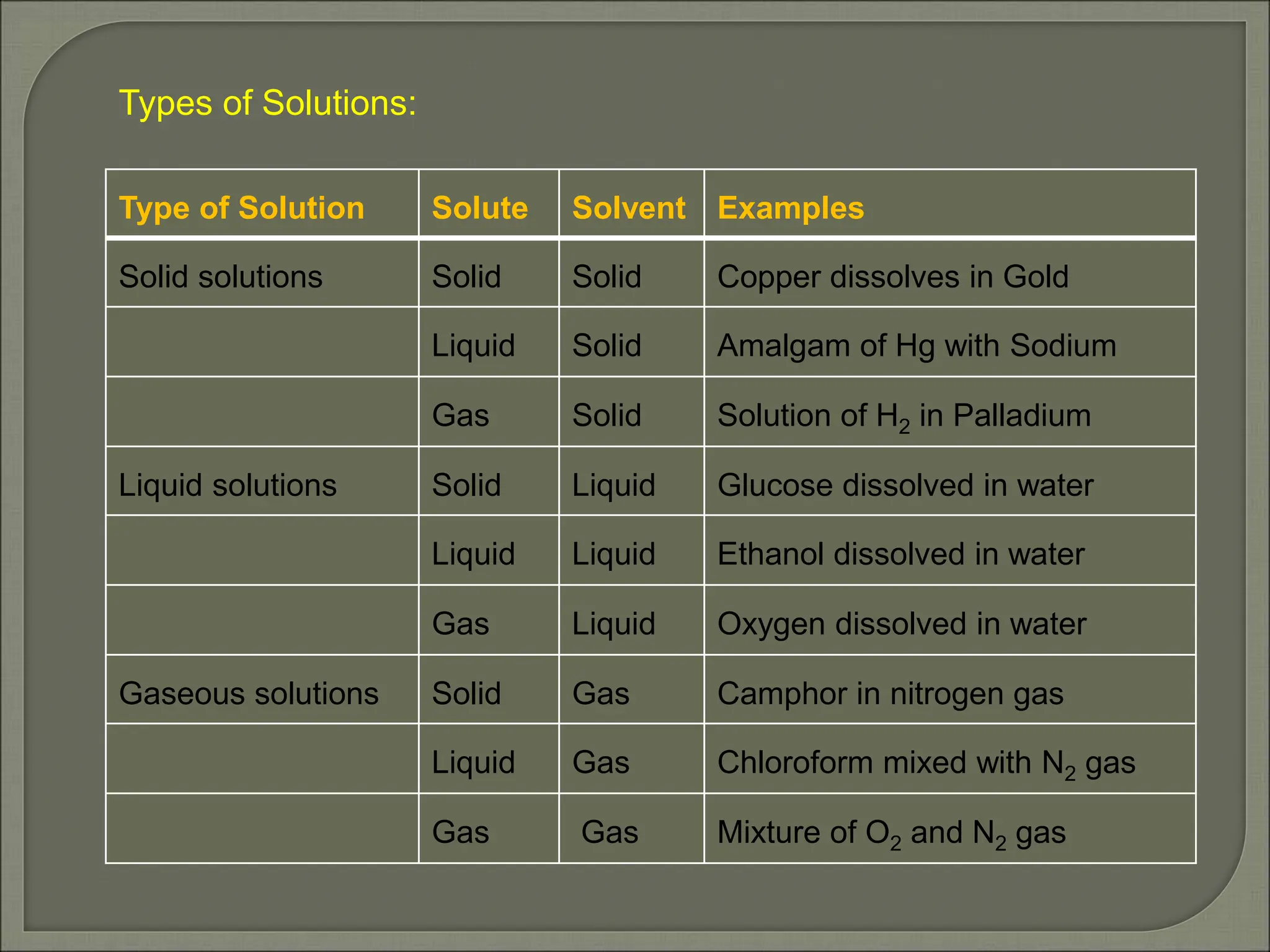
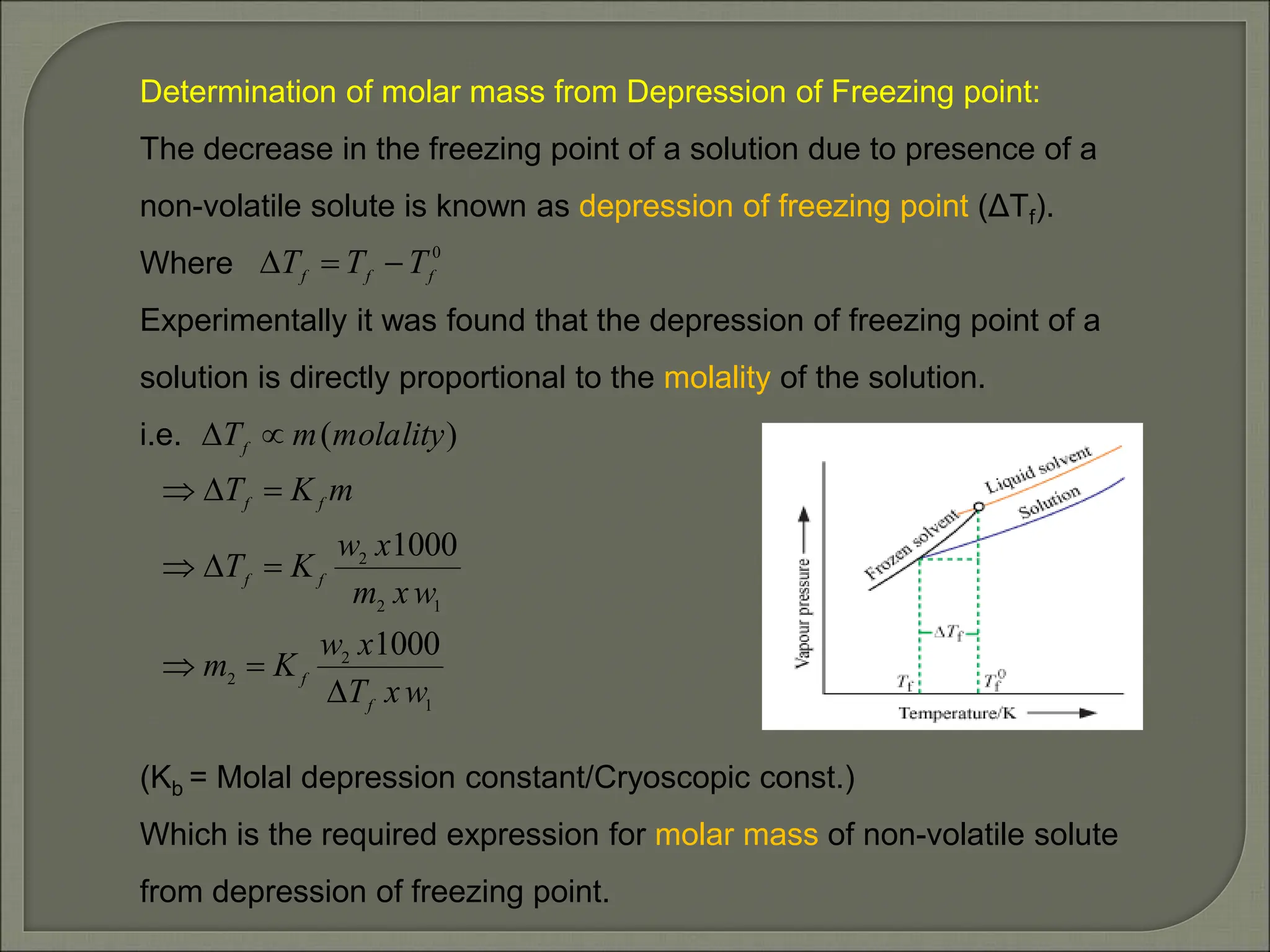
This document provides an overview of solutions and related concepts in chemistry. It begins by defining a solution as a homogeneous mixture of two or more components. It then discusses different types of solutions and various ways of expressing the concentration of solutions, including mass percentage, molarity, and molality. Key concepts covered include solubility, Raoult's law, ideal and non-ideal solutions, and azeotropes. Vapour pressure and Henry's law are also summarized in relation to gas solubility in liquids. The document aims to cover important learning objectives about solutions for a class 12 chemistry course in India.

1. A
PRESENTATION
ON
UNIT – 1: SOLUTIONS
CLASS – XII, CHEMISTRY (NCERT)

2. Learning Objectives:
• Solutions and types of solutions
• Expressing Concentration of solutions
• Solubility- Solids and Gases in liquids
• Vapour pressure of solutions
• Ideal and Non ideal solutions
• Colligative properties and determination of molar mass
• Abnormal colligative properties

3. Solution:
 Solution is a homogeneous mixture of two or more
components which has uniform position and show
identical properties through out the phase.
 The component which is present in large quantity is
known as solvent and the other components are called
solutes.
 A solution which consists of only two components is
known a binary solution.

4. Types of Solutions:
Type of Solution Solute Solvent Examples
Solid solutions Solid Solid Copper dissolves in Gold
Liquid Solid Amalgam of Hg with Sodium
Gas Solid Solution of H2 in Palladium
Liquid solutions Solid Liquid Glucose dissolved in water
Liquid Liquid Ethanol dissolved in water
Gas Liquid Oxygen dissolved in water
Gaseous solutions Solid Gas Camphor in nitrogen gas
Liquid Gas Chloroform mixed with N2 gas
Gas Gas Mixture of O2 and N2 gas

5. Expression of Concentration of Solutions:
 The amount of solute present in a solution is called its
concentration.
 Concentration of solutions can be expressed in 7 ways
• Mass percentage ( w / w % )
• Volume percentage ( v / v % )
• Mass by volume percentage ( w / v % )
• Parts per million ( ppm )
• Mole fraction ( X )
• Molarity ( M )
• Molality ( m )

6. Mass percentage:
The number of grams of solute present in 100g of solution is known
mass percentage.
Volume percentage:
The volume of solute (in mL) present in 100 mL of solution is known
as volume percentage.
Mass by volume percentage:
The number of grams of solute present in 100 mL of solution is known
as mass by volume percentage.
100
%
/ x
solution
the
of
Mass
solute
the
of
Mass
w
w 
100
%
/ x
solution
the
of
Volume
solute
the
of
Volume
v
v 
100
%
/ x
solution
the
of
Volume
solute
the
of
Mass
v
w 

7. Parts per million:
The number of parts of solute present in 106 (1 million) parts of
solution is known as parts per million. This unit used when solute is
present in trace amounts.
Mole fraction:
The ratio of number of moles of one component (solute) to the total
number of moles of all components (solution) is known as mole
fraction.
and
6
10
x
components
all
partsof
of
number
Total
nt
onecompone
partsof
of
Number
ppm 
solution
of
moles
of
number
total
solute
of
moles
of
Number
x
solute
of
fraction
Mole solute 
)
(
solvent
solute
solute
solute
n
n
n
x


solvent
solute
solvent
solvent
n
n
n
x


1



 solution
solvent
solute x
x
x

8. Molarity:
The number of moles of solute present in one litre of solution is known
as molarity. It is represented by ‘M’ and expressed in mol.L–1.
Molality:
The number of moles of solute present in one kilogram of solvent is
known as molality. It is represented by ‘m’ and expressed in mol.kg–1.
)
(
)
(
1000
)
(
)
(
.
.
)
(
2
2
VmL
solution
of
volume
x
m
solute
of
mass
molar
x
w
solute
of
mass
M
molarity
e
i
Litres
in
solution
of
Volume
solute
of
moles
of
Number
M
Molarity


)
(
)
(
1000
)
(
)
(
.
.
)
(
1
2
2
kg
w
solvent
of
mass
x
m
solute
of
mass
molar
x
w
solute
of
mass
m
molality
e
i
ograms
kil
in
solvent
of
Mass
solute
of
moles
of
Number
m
Molality



9. Solubility:
1. The maximum amount of solute that can be dissolved in 100
grams of solvent at a given temperature is known as its solubility.
The solubility of a solid, liquid or gas depends upon its nature,
temperature and pressure.
2. The solubility of a solute in a solvent is possible when the
intermolecular interactions are similar.
3. A solution in which no more solute can be dissolved at the same
temperature is known as a saturated solution.
4. In such solutions a dynamic equilibrium exists between dissolved
solute particles and undissolved solute particles.
5. A solution which can dissolve more amount of solute at the same
temperature is known as an unsaturated solution.
6. A solution in which more amount of solute can be dissolved by
increasing the temperature is known as a super saturated solution.
Such solutions contain more amount of solute than it could be
dissolved by the solvent under normal conditions.

10. Solubility of a solid in a liquid:
• The solubility of a solid solute in a liquid solvent mainly depends
upon temperature.
• In general, the solubility of a solid in liquid increases with increase
in temperature.
• If the dissolution process is endothermic then the solubility
increases with increase in temperature.
• If the dissolution process is exothermic then the solubility decrease
with increasing temperature.
• Pressure does not have any significant effect.
Solubility of a gas in a liquid:
• The solubility of a gas in a liquid solvent mainly depends upon both
temperature and pressure.
• The solubility of a gas in a liquid decreases with increase in
temperature.
• The solubility of a gas in a liquid increases with increase in
pressure.

11. Henry’s law:
It states that “the partial pressure of a gas in vapour phase (p) is
proportional to the mole fraction of the gas (x) in the solution”
Mathematically…
 Where KH is the Henry’s law constant , which is different for different
gases.
 Higher the value of KH, lower is the solubility of the gas at a given
pressure ( ).
Applications:
• Aquatic animals are more comfortable in cold water rather than in
warm water because cold water contains more amount of dissolved
oxygen. ( solubility varies inversely with temp.)
• Soda bottles are sealed under high pressure, to increase the
solubility of CO2 gas in soft drinks / soda water.( solubility α pressure)
• The oxygen tanks used by scuba divers are diluted with helium to
avoid a medical condition known as bends.
• People living at high altitudes suffer with a medical condition anoxia
due to low solubility of oxygen in blood.
x
K
p
x
p
H



x
K
x
p
K H
H
1




12. Vapour pressure:
• The pressure exerted by vapour of a liquid at its equilibrium state is
known as vapour pressure.
• The vapour pressure of a liquid increases with increase in
temperature and decreases with increase in pressure.
Raoult’s law for solutions containing volatile solutes:
It states that ‘‘ For a solution of volatile liquids, the partial vapour
pressure of each component is directly proportional to its mole fraction’’
Mathematically…
Where are the vapour pressures of pure liquids 1 & 2
respectively at the same temperature.
Note:
• According to Dalton’s law of partial pressure;
• For vapour phase;
• Raoult’s law becomes a special case of Henry’s law when KH = p0
2
0
2
2
1
0
1
1
2
2
1
1
x
p
p
and
x
p
p
x
p
and
x
p





0
2
0
1 p
and
p
0
1
2
0
1
0
2
2
0
2
1
0
1
2
1
)
( p
x
p
p
p
x
p
x
p
p
p
p
p
total
total
total









total
total
p
y
p
p
y
p
2
2
1
1



13. Raoult’s law for solution containing non-volatile solute:
It states that “ the partial pressure of a solvent over a solution
containing non volatile is proportional to the mole fraction of the
solvent”
Mathematically, Let the partial pressure of the solution = Ps
and mole fraction of the solvent = Xsolvent
According to Raoult’s law;
( p0 = p.v.p.of pure solvent )
In other words, it can be stated as ‘ The relative lowering vapour
pressure of a solution is equal to the mole fraction of the solute’
solute
s
solvent
s
solvent
s
solvent
s
solvent
s
x
p
p
p
x
p
p
x
p
p
x
p
p
x
p












0
0
0
0
0
1
1

14. Liquid-liquid solutions can be classified into Ideal and non-ideal
solutions on basis of Raoult’s law.
Ideal solutions:
• The solutions which obey Raoult’s law over the entire range of
concentration are known as ideal solutions.
• In case of ideal solutions, the intermolecular forces between
solute-solute, solvent-solvent and solute-solvent are nearly same.
• For ideal solutions;
Examples: Solution of (a) n-Hexane and n-Heptane
(b) Benzene and toluene
(c) Bromoethane and chloroethane
0
0 


 mix
mix V
and
H

15. Non-ideal solutions:
• The solutions which does not obey Raoult’s law over the entire range of
concentration are known as non-ideal solutions.
• Incase of non-ideal solutions, the interactions between solute- solute and
solvent-solvent is not equal to that of solute-solvent.
• For non-ideal solutions;
• In such solutions, the vapour pressure is either higher or lower than that
predicted by Raoult’s law.
• It the vapour pressure is higher, then the solution shows positive deviation.
• It the vapour pressure is lower, then the solution shows negative deviation.
• So, non-ideal solutions are further classified into two types.
0
0 


 mix
mix V
and
H

16. Positive deviation:
The non-ideal solutions in which the intermolecular attractive forces
between solute-solvent molecules are weaker than that of solute-solute
and solvent-solvent molecules show positive deviation from Raoult’s law.
Incase of positive deviation, the vapour pressure of the solution is always
higher than that predicted from Raoult’s law.
Examples: Mixture of (a) Ethanol and Acetone (b) CS2 and Acetone
Negative deviation:
The non-ideal solutions in which the intermolecular attractive forces
between solute-solvent molecules are stronger than that of solute-solute
and solvent-solvent molecules show negative deviation from Raoult’s law.
Incase of negative deviation, the vapour pressure of the solution is always
lower than that predicted from Raoult’s law.
Examples: Mixture of (a) Phenol and Aniline (b) Chloroform and Acetone

17. Azeotropes:
The binary solutions having same composition in liquid and vapour
phase which boil at a constant temperature and cannot be separated
by fractional distillation are known as azeotropes.
Minimum boiling Azeotrope:
The binary solutions which show a large positive deviation from
Raoult’s law form minimum boiling azetrope at a specific composition.
Examples: Ethanol (95%) and Water (5%) mixture.
Maximum boiling Azeotrope:
The binary solutions which show a large negative deviation from
Raoult’s law form maximum boiling azetrope at a specific composition.
Examples: Nitric acid (68%) and Water (32%) mixture.

18. Colligative properties and determination of molar mass:
The properties which depends upon the number of solute particles
present in the solution are known as colligative properties.
There are four types of colligative properties mainly observed. i.e.
(a) Relative lowering in vapour pressure
(b) Elevation of boiling point
(c) Depression of freezing point
(d) Osmotic pressure
Special Note:
P0–Ps = lowering in vapour pressure of the solution
( P0–Ps) / P0 = Relative lowering in vapour pressure of the solution
Tb = Boiling temperature of solution
Tb
0 = Boiling temperature of pure solvent

19. Determination of molar mass from Relative lowering in vapour pressure:
From Raoult’s law for solutions containing non-volatile solutes,
We know that;
( for very dilute solutions nsolute is negligible)
Which is the required expression for molar mass of non-volatile solute from
the relative lowering in vapour pressure
1
1
2
2
1
2
1
2
0
0
0
0
0
0
0
0
w
x
RLVP
m
x
w
m
w
x
m
m
x
w
p
p
p
n
n
p
p
p
n
n
n
p
p
p
x
p
p
p
s
solvent
solute
s
solvent
solute
solute
s
solute
s















20. Determination of molar mass from Elevation of Boiling point:
The increase in the boiling point of a solution due to presence of a
non-volatile solute is known as elevation of boiling point (ΔTb).
Where
Experimentally it was found that the elevation of boiling point of a
solution is directly proportional to the molality of the solution.
i.e.
(Kb = Molal elevation constant/Ebullioscopic const.)
Which is the required expression for molar mass of non-volatile solute
from elevation of boiling point.
1
2
2
1
2
2
1000
1000
)
(
w
x
T
x
w
K
m
w
x
m
x
w
K
T
m
K
T
molality
m
T
b
b
b
b
b
b
b











0
b
b
b T
T
T 



21. Determination of molar mass from Depression of Freezing point:
The decrease in the freezing point of a solution due to presence of a
non-volatile solute is known as depression of freezing point (ΔTf).
Where
Experimentally it was found that the depression of freezing point of a
solution is directly proportional to the molality of the solution.
i.e.
(Kb = Molal depression constant/Cryoscopic const.)
Which is the required expression for molar mass of non-volatile solute
from depression of freezing point.
0
f
f
f T
T
T 


1
2
2
1
2
2
1000
1000
)
(
w
x
T
x
w
K
m
w
x
m
x
w
K
T
m
K
T
molality
m
T
f
f
f
f
f
f
f












22. Determination of molar mass from Osmotic pressure:
The excess pressure which must be applied on the solution side just to
stop the flow of pure solvent towards the solution side when both are
separated by a semi permeable membrane is called osmotic pressure.
It is represented by .
Experimentally it was found that osmotic pressure of a solution is
directly proportional to the molarity of the solution and temperature.
i.e.
( R = universal gas constant = 0.082L bar mol–1K–1)
Which is the required expression for molar mass of non-volatile solute
from osmotic pressure.
V
RT
w
m
RT
m
w
RT
n
V
RT
V
n
CRT
CT
T
and
C
solute
solute




















2
2
2
2


23. Osmosis:
The spontaneous flow of solvent molecules towards the solution side
when both are separated by a semi permeable membrane is called
osmosis.
Osmotic pressure:
The excess pressure which must be applied on the solution side in order
to stop osmosis process (the flow of solvent towards the solution side
when both are separated by a semi permeable membrane) is known as
osmotic pressure.
Reverse osmosis:
When a pressure larger than osmotic pressure is applied on the solution
side then pure solvent flows out of the solution through the semi
permeable membrane. This process is called reverse osmosis.
Isotonic solutions:
Two solutions having same osmotic pressure at a given temperature are
called isotonic solutions. Between such solutions no osmosis occurs.
• out of two, if one solution have higher osmotic pressure then it is called
hypertonic solution and the other solution is called hypotonic solution.

24. Abnormal molar mass:
The molar mass calculated on the basis of colligative properties (such
as elevation of boiling point, depression of freezing point, osmotic
pressure or relative lowering in vapour pressure) is either lower or
higher than the normal value is called as abnormal molar mass.
van’t Hoff factor:
The ratio of normal molar mass and abnormal molar mass is known as
van’t Hoff factor. It is presented by ‘ i ’, which accounts the extent of
dissociation or association.
on
dissociati
n
associatio
before
particles
of
moles
of
No
on
dissociati
n
associatio
after
particles
of
moles
of
No
mass
molar
Abnormal
mass
molar
Normal
i
factor
Hoff
t
van
/
.
/
.
)
(
'



25. Note:
In case of Association;
In case of Dissociation;
So, colligative properties can be expressed in terms of van’t Hoff factor as
Relative lowering in vapour pressure:
Elevation of Boiling point :
Depression of Freezing point :
Osmotic pressure : RT
n
i
V
m
K
i
T
m
K
i
T
n
n
i
p
p
p
f
f
b
b
s
2
1
2
0
0
.
.
.
/
.
/
)
(








1
1


i
i
Prepared by
R Baikuntha Rao
PGT Chemistry
DAV Public School, Berhampur.