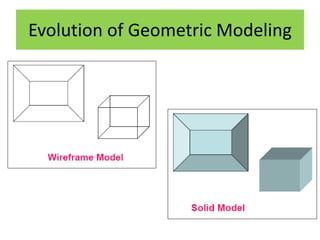
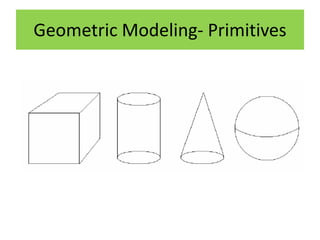
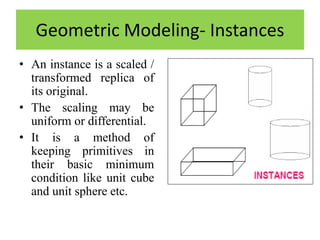
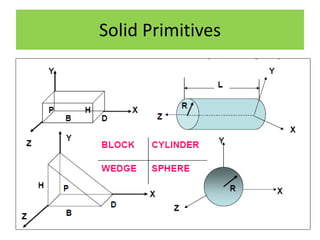
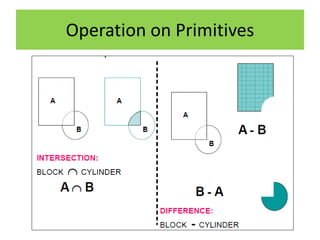
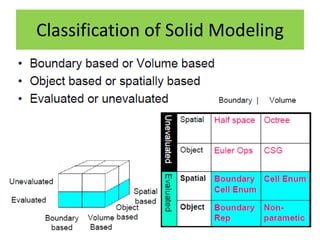
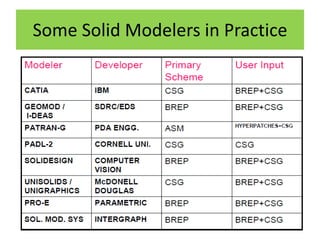
Solid models provide more complete representations of objects than surface or wireframe models by including topological information about connectivity in addition to geometric information. Solid models allow for accurate design and further automation in manufacturing. They represent objects fully using primitives that can be combined through Boolean operations. Major solid modeling schemes include boundary representation, constructive solid geometry, and sweeping which use primitives, instances, and operations on primitives to build valid solid models.

1. Solid Models
R.B.Chadge

2. Evolution of Geometric Modeling
• A wireframe representation of an object is done using
edges (lines curves) and vertices.
• Surface representation is the logical evolution using faces
(surfaces), edges and vertices.
• In this sequence of developments, the solid modeling uses
topological information in addition to the geometrical
information to represent the object completely.

3. Evolution of Geometric Modeling

4. Advantages of Solid Models
• Unlike wireframes and surface representations which
contain only geometrical data,
• The solid model uses topological information in
addition to the geometrical information to represent
the object completely.
• Solid model results in accurate design, helps to
further the goal of CAD/ CAM like CIM, Flexible
manufacturing leading to better automation of the
manufacturing process.

5. Advantages of Solid Models
• Geometry: The graphical information of dimension,
length, angle, area and transformations
• Topology: The invisible information about the
connectivity, neighbourhood, associatively etc.

6. Definition of Solid Model
• A solid model of an object is a more complete
representation than its surface (wireframe) model.
• It provides more topological information in addition
to the geometrical information which helps to
represent the solid completely.

7. Geometric Modeling- Primitives

8. Geometric Modeling- Instances
• An instance is a scaled /
transformed replica of
its original.
• The scaling may be
uniform or differential.
• It is a method of
keeping primitives in
their basic minimum
condition like unit cube
and unit sphere etc.

9. Solid Primitives

10. Operation on Primitives
• A desired solid can be obtained by combining two or
more solids.
• When we use Boolean (set) operations the validity of
the third (resulting) solid is ensured.

11. Operation on Primitives

12. • Rigidity: Shape of the solid is invariant w.r.t location
/orientation.
• Homogeneous 3-dimensionality: The solid
boundaries must be in contact with the interior. No
isolated and dangling edges are permitted.
Properties of Solid Models

13. • Finiteness and finite describability: Size is finite and a
finite amount of information can describe the solid
model.
• Closure under rigid motion and regularised Boolean
operations: Movement and Boolean operations
should produce other valid solids.
• Boundary determinism: The boundary must contain
the solid and hence determine the solid distinctly.
Properties of Solid Models

14. Classification of Solid Modeling

15. 1. Half Spaces.
2. Boundary Representation (B-Rep)
3. Constructive Solid Geometry (CSG)
4. Sweeping
5. Analytical Solid Modeling (ASM)
6. Cell decomposition
7. Spatial Ennumeration
8. Octree encoding
9. Primitive Instancing
The 3 most popular schemes: B-rep, CSG, Sweeping
Major Modeling Schemes

16. Conversion Among Representations
• Some representations can be converted to other
representations.
• CSG to B-REP (but not B-rep to CSG)

17. Some Solid Modelers in Practice