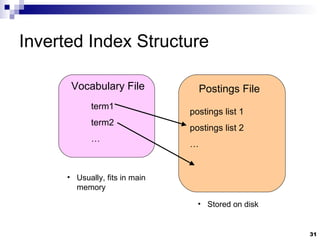
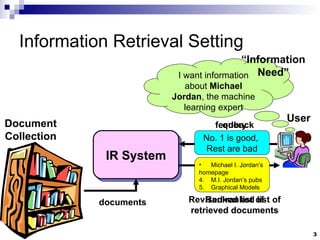
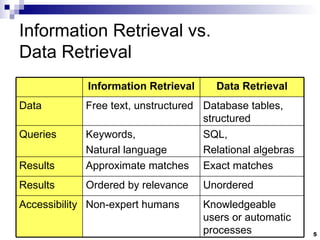
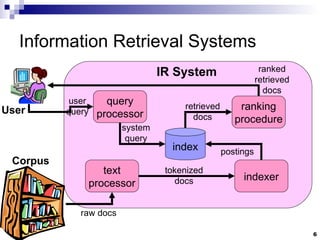
This document summarizes key concepts in information retrieval systems and algorithms for large data sets. It discusses the differences between information retrieval and data retrieval systems. It also describes several classic models for relevance ranking in IR, including the Boolean model and vector space model. The document outlines topics like text processing, indexing, searching, and evaluation in information retrieval systems.

1. Algorithms for Large Data Sets Ziv Bar-Yossef Lecture 2 March 26, 2006 http://www.ee.technion.ac.il/courses/049011

2. Information Retrieval

3. Information Retrieval Setting I want information about Michael Jordan , the machine learning expert query User Document Collection “ Information Need” +”Michael Jordan” -basketball Michael I. Jordan’s homepage NBA.com Michael Jordan on TV Ranked list of retrieved documents IR System documents No. 1 is good, Rest are bad feedback Revised ranked list of retrieved documents Michael I. Jordan’s homepage M.I. Jordan’s pubs Graphical Models

4. Information Retrieval vs. Data Retrieval Information Retrieval System: a system that allows a user to retrieve documents that match her “information need” from a large corpus. Ex: Get documents about Michael Jordan, the machine learning expert. Data Retrieval System: a system that allows a user to retrieve all documents that match her query from a large corpus. Ex: SELECT doc FROM corpus WHERE (doc.text CONTAINS “Michael Jordan”) AND NOT (doc.text CONTAINS “basketball”).

5. Information Retrieval vs. Data Retrieval Database tables, structured Free text, unstructured Data Knowledgeable users or automatic processes Non-expert humans Accessibility Unordered Ordered by relevance Results Exact matches Approximate matches Results SQL, Relational algebras Keywords, Natural language Queries Data Retrieval Information Retrieval

6. Information Retrieval Systems IR System query processor text processor user query ranked retrieved docs User Corpus ranking procedure system query retrieved docs index indexer tokenized docs postings raw docs

7. Search Engines Search Engine query processor text processor user query ranked retrieved docs User Web ranking procedure system query retrieved docs index indexer tokenized docs postings crawler global analyzer repository

8. Classical IR vs. Web IR Hypertext Text Documents Large Small # of matches Partially accessible Accessible Data accessibility Huge Large Volume Link-based Content-based IR techniques Widely diverse Homogeneous Format diversity In flux Infrequent Data change rate Noisy, dups Clean, no dups Data quality Web IR Classical IR

9. Outline Abstract formulation Models for relevance ranking Retrieval evaluation Query languages Text processing Indexing and searching

10. Abstract Formulation Ingredients: D: document collection Q: query space f: D x Q  R : relevance scoring function For every q in Q, f induces a ranking (partial order)  q on D Functions of an IR system: Preprocess D and create an index I Given q in Q, use I to produce a permutation  on D Goals: Accuracy:  should be “close” to  q Compactness: index should be compact Response time: answers should be given quickly

11. Document Representation T = { t 1 ,…, t k }: a “token space” (a.k.a. “feature space” or “term space”) Ex: all words in English Ex: phrases, URLs, … A document: a real vector d in R k d i : “weight” of token t i in d Ex: d i = normalized # of occurrences of t i in d

12. Classic IR (Relevance) Models The Boolean model The Vector Space Model (VSM)

13. The Boolean Model A document: a boolean vector d in {0,1} k d i = 1 iff t i belongs to d A query: a boolean formula q over tokens q: {0,1} k  {0,1} Ex: “Michael Jordan” AND (NOT basketball) Ex: +“Michael Jordan” –basketball Relevance scoring function: f(d,q) = q(d)

14. The Boolean Model: Pros & Cons Advantages: Simplicity for users Disadvantages: Relevance scoring is too coarse

15. The Vector Space Model (VSM) A document: a real vector d in R k d i = weight of t i in d (usually TF-IDF score) A query: a real vector q in R k q i = weight of t i in q Relevance scoring function: f(d,q) = sim(d,q) “ similarity” between d and q

16. Popular Similarity Measures L 1 or L 2 distance d,q are first normalized to have unit norm Cosine similarity d q d –q  d q

17. TF-IDF Score: Motivation Motivating principle: A term t i is relevant to a document d if: t i occurs many times in d relative to other terms that occur in d t i occurs many times in d relative to its number of occurrences in other documents Examples 10 out of 100 terms in d are “java” 10 out of 10,000 terms in d are “java” 10 out of 100 terms in d are “the”

18. TF-IDF Score: Definition n(d,t i ) = # of occurrences of t i in d N =  i n(d,t i ) (# of tokens in d) D i = # of documents containing t i D = # of documents in the collection TF(d,t i ): “Term Frequency” Ex: TF(d,t i ) = n(d,t i ) / N Ex: TF(d,t i ) = n(d,t i ) / (max j { n(d,t j ) }) IDF(t i ): “Inverse Document Frequency” Ex: IDF(t i ) = log (D/D i ) TFIDF(d,t i ) = TF(d,t i ) x IDF(t i )

19. VSM: Pros & Cons Advantages: Better granularity in relevance scoring Good performance in practice Efficient implementations Disadvantages: Assumes term independence

20. Retrieval Evaluation Notations: D: document collection D q : documents in D that are “relevant” to query q Ex: f(d,q) is above some threshold L q : list of results on query q D L q D q Recall: Precision:

21. Recall & Precision: Example Recall(A) = 80% Precision(A) = 40% d 123 d 84 d 56 d 6 d 8 d 9 d 511 d 129 d 187 d 25 List A Relevant docs: d 123 , d 56 , d 9 , d 25 , d 3 d 81 d 74 d 56 d 123 d 511 d 25 d 9 d 129 d 3 d 5 List B Recall(B) = 100% Precision(B) = 50%

22. Precision@k and Recall@k Notations: D q : documents in D that are “relevant” to q L q,k : top k results on the list Recall@k: Precision@k:

23. Precision@k: Example d 123 d 84 d 56 d 6 d 8 d 9 d 511 d 129 d 187 d 25 List A d 81 d 74 d 56 d 123 d 511 d 25 d 9 d 129 d 3 d 5 List B

24. Recall@k: Example d 123 d 84 d 56 d 6 d 8 d 9 d 511 d 129 d 187 d 25 List A d 81 d 74 d 56 d 123 d 511 d 25 d 9 d 129 d 3 d 5 List B

25. “ Interpolated” Precision Notations: D q : documents in D that are “relevant” to q r: a recall level (e.g., 20%) k(r): first k so that recall@k >= r Interpolated precision@ recall level r = max { precision@k : k >= k(r) }

26. Precision vs. Recall: Example d 123 d 84 d 56 d 6 d 8 d 9 d 511 d 129 d 187 d 25 List A d 81 d 74 d 56 d 123 d 511 d 25 d 9 d 129 d 3 d 5 List B

27. Query Languages: Keyword-Based Singe-word queries Ex: Michael Jordan machine learning Context queries Phrases. Ex: “Michael Jordan” “machine learning” Proximity. Ex: “Michael Jordan” at distance of at most 10 words from “machine learning” Boolean queries Ex: +”Michael Jordan” –basketball Natural language queries Ex: “Get me pages about Michael Jordan, the machine learning expert.”

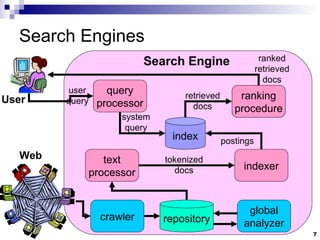
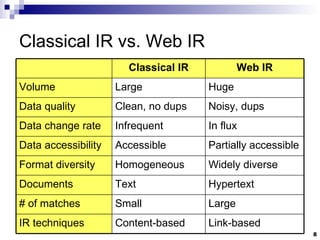
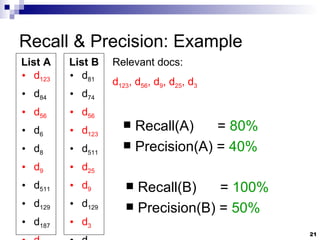
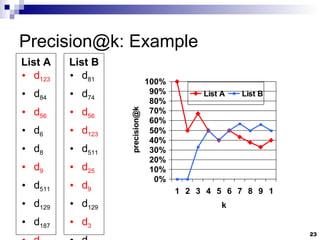
28. Query Languages: Pattern Matching Prefixes Ex: prefix:comput Suffixes Ex: suffix:net Regular Expressions Ex: [0-9]+th world-wide web conference

29. Text Processing Lexical analysis & tokenization Split text into words, downcase letters, filter out punctuation marks, digits, hyphens Stopword elimination Better retrieval accuracy, more compact index Ex: “to be or not to be” Stemming Ex: “computer”, “computing”, “computation”  comput Index term selection Keywords vs. full text

30. Inverted Index Michael 1 Jordan 2 , the 3 author 4 of 5 “graphical 6 models 7 ”, is 8 a 9 professor 10 at 11 U.C. 12 Berkeley 13 . The 1 famous 2 NBA 3 legend 4 Michael 5 Jordan 6 liked 7 to 8 date 9 models 10 . d 1 d 2 author: (d 1 ,4) berkeley: (d 1 ,13) date: (d 2 ,9) famous: (d 2 , 2) graphical: (d 1 ,6) jordan: (d 1 ,2), (d 2 ,6) legend: (d 2 ,4) like: (d 2 ,7) michael: (d 1 ,1), (d 2 ,5) model: (d 1 ,7), (d 2 ,10) nba: (d 2 ,3) professor: (d 1 ,10) uc: (d 1 ,12) Vocabulary Postings

31. Inverted Index Structure Vocabulary File term1 term2 … Postings File postings list 1 postings list 2 … Usually, fits in main memory Stored on disk

32. Searching an Inverted Index Given: t 1 , t 2 : query terms L 1 ,L 2 : corresponding posting lists Need to get ranked list of docs in intersection of L 1 ,L 2 Solution 1: If L 1 ,L 2 are comparable in size, “merge” L 1 and L 2 to find docs in their intersection, and then order them by rank. (running time: O(|L 1 | + |L 2 |)) Solution 2: If L 1 is considerably shorter than L 2 , binary search each posting of L 1 in L 2 to find the intersection, and then order them by rank. (running time: O(|L 1 | x log(|L 2 |))

33. Search Optimization Improvement: Order docs in posting lists by static rank (e.g., PageRank). Then, can output top matches, without scanning the whole lists.

34. Index Construction Given a stream of documents, store (did,tid,pos) triplets in a file Sort and group file by tid Extract posting lists

35. Index Maintenance Naïve updates of inverted index can be very costly Require random access A single change may cause many insertions/deletions Batch updates Two indices Main index (created in batch, large, compressed) “ Stop-press” index (incremental, small, uncompressed)

36. Index Maintenance If a page d is inserted/deleted, the “signed” postings (did,tid,pos,I/D) are added to the stop-press index. Given a query term t , fetch its list L t from main index, and two lists L t,+ and L t,- from stop-press index. Result is: When stop-press index grows too large, it is merged into the main index.

37. Index Compression Delta compression Saves a lot for popular terms Doesn’t save much for rare terms (but these don’t take much space anyway) michael: (1000007,5), (1000009,12), (1000013,77), (1000035,88),… michael: (1000007,5), (2,12), (4,77), (22,88),…

38. Variable Length Encodings How to encode gaps succinctly? Option 1: Fixed-length binary encoding. Effective when all gap lengths are equally likely No savings over storing doc ids. Option 2: Unary encoding. Gap x is encoded by x-1 1’s followed by a 0 Effective when large gaps are very rare (Pr(x) = 1/2 x ) Option 3: Gamma encoding. Gap x is encoded by (  x  x ), where  x is the binary encoding of x and  x is the length of  x , encoded in unary. Encoding length: about 2log(x).

39. End of Lecture 2