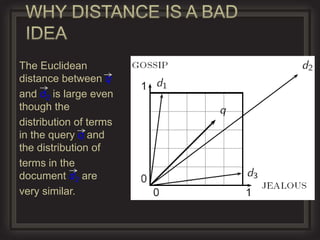
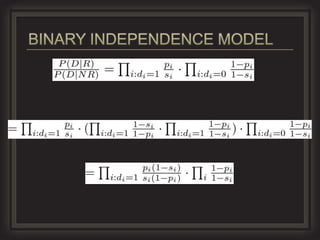
The document discusses probabilistic retrieval models in information retrieval. It provides an overview of older models like Boolean retrieval and vector space models. The main focus is on probabilistic models like BM25 and language models. It explains key concepts in probabilistic IR like the probability ranking principle, using Bayes' rule to estimate the probability that a document is relevant given features of the document, and estimating probabilities based on the frequencies of terms in relevant documents. The goal is to rank documents based on the probability of relevance to the query.

1. Probabilistic Retrieval Models
Lecture 8
Sean A. Golliher

2.  Need to quickly cover some old material
to understand the new methods

3.  Complex concept that has been studied for
some time
 Many factors to consider
 People often disagree when making relevance
judgments
 Retrieval models make various assumptions
about relevance to simplify problem
 e.g., topical vs. user relevance
 e.g., binary vs. multi-valued relevance

4.  Older models
 Boolean retrieval
 Vector Space model
 Probabilistic Models
 BM25
 Language models
 Combining evidence
 Inference networks
 Learning to Rank

5.  Two possible outcomes for query
processing
 TRUE and FALSE
 “exact-match” retrieval
 simplest form of ranking
 Query usually specified using Boolean
operators
 AND, OR, NOT

6.  Advantages
 Results are predictable, relatively easy to
explain
 Many different features can be incorporated
 Efficient processing since many documents
can be eliminated from search
 Disadvantages
 Effectiveness depends entirely on user
 Simple queries usually don’t work well
 Complex queries are difficult

7.  Documents and query represented by a
vector of term weights
 Collection represented by a matrix of
term weights

9.  3-d pictures useful, but can be
misleading for high-dimensional space

10. The Euclidean
distance between q
and d2 is large even
though the
distribution of terms
in the query q and
the distribution of
terms in the
document d2 are
very similar.

11.  Thought experiment: take a document d and
append it to itself. Call this document d′.
 “Semantically” d and d′ have the same content
 The Euclidean distance between the two
documents can be quite large
 The angle between the two documents is 0,
corresponding to maximal similarity (cos(0) = 1).
 Key idea: Rank documents according to angle with
query.

12.  In Euclidean space, define dot product of
vectors a & b as
ab=||a|| ||b|| cos a
where b
||a|| == length
== angle between a & b

13.  By using Law of Cosines, can compute
coordinate-dependent definition in 3-
space:
 ab= axbx + ayby + azbz
 cos = ab/||a|| ||b||
 cosine(0) = 1
 cosine(90 deg) = 0

14.  Documents ranked by distance between
points representing query and documents
 Similarity measure more common than a
distance or dissimilarity measure
 e.g. Cosine correlation

15.  Consider two documents D1, D2 and a query
Q
○ D1 = (0.5, 0.8, 0.3), D2 = (0.9, 0.4, 0.2), Q = (1.5, 1.0, 0)

16. Dot product Unit vectors
    V
  q d q d q di
i 1 i
cos(q, d )    
q d q d V 2
q
V
d i2
i 1 i i 1
qi is the tf-idf weight of term i in the query
di is the tf-idf weight of term i in the document
cos(q,d) is the cosine similarity of q and d … or,
equivalently, the cosine of the angle between q and d.

17.  tf.idf weight (older retrieval model)
 tf: term frequency of term over collection of
documents
 idf: inverse document freq. ex:
○ log(N/n)
 N is the total number of document
 n is total number of documents that contain a term
 Measure of “importance” of term. The more documents a
term appears in the lest discriminating the term is.
 Use log to dampen the effects

18.  The collection frequency of t is the
number of occurrences of t in the
collection, counting multiple occurrences.
Word Collection frequency Document frequency
insurance 10440 3997
try 10422 8760
 Document frequency df is number of
documents that contain a term t.
 Which of these is more useful?

19.  The tf-idf weight of a term is the product of its
tf weight and its idf weight.
 Best known weighting scheme in information retrieval
○ Note: the “-” in tf-idf is a hyphen, not a minus sign!
○ Alternative names: tf.idf, tf x idf
 Increases with the number of occurrences within a
document
 Increases with the rarity of the term in the collection

20.  Rocchio algorithm (paper topic)
 Optimal query
 Maximizes the difference between the average
vector representing the relevant documents and
the average vector representing the non-relevant
documents
 Modifies query according to
 α, β, and γ are parameters
○ Typical values 8, 16, 4

21.  Most dominant paradigm used today
 Probability theory is a strong foundation
for representing uncertainty that is
inherent in IR process.

22.  Robertson (1977)
If a reference retrieval system’s response to each
request is a ranking of the documents in the
collection in order of decreasing probability of
relevance to the user who submitted the request,
where the probabilities are estimated as
accurately as possible on the basis of whatever
data have been made available to the system for
this purpose, the overall effectiveness of the
system to its user will be the best that is obtainable
on the basis of those data.”

23.  Probability Ranking Principle (Robertson, 70ies;
Maron, Kuhns, 1959)
 Information Retrieval as Probabilistic Inference
(van Rijsbergen & co, since 70ies)
 Probabilistic Indexing (Fuhr & Co.,late 80ies-
90ies)
 Bayesian Nets in IR (Turtle, Croft, 90ies)
 Probabilistic Logic Programming in IR (Fuhr &
co, 90ies)

24.  P(a | b) => Conditional probability. Probability of a given
that b occurred.
 Basic definitions
(a È b) => AorB
(a Ç b) = AandB

25. Let a, b be two events.
p(a | b)p(b) = p(a Ç b) = p(b | a)p(a)
p(b | a)p(a)
p(a | b) =
p(b)
p(a | b)p(b) = p(b | a)p(a)

26.  Let D be a document in the collection.
 Let R represent relevance of a document w.r.t. given
(fixed) query and let NR represent non-relevance.
 How do we find P(R|D)? Probability that a retrieved
document is relevant. Abstract concept.
 P(R) is the probability that a retrieved is relevant
 Not Clear how to calculate this.

27.  Can we calculate P(D|R)? Probability of a document
occurring in a set given a relevant set has been returned.
 If we KNOW we have relevant set of documents (maybe
from humans?) We could calculate how often specific
words occur in a certain set.

29. Let D be a document in the collection.
Let R represent relevance of a document w.r.t. given (fixed)
query and let NR represent non-relevance.
Need to find p(R|D) - probability that a retrieved document D
is relevant.
p(D | R)p(R) p(R),p(NR) - prior probability
p(R | D) =
p(D) of retrieving a (non) relevant
p(xD | NR)p(NR) document
p(NR | D) =
p(xD)
P(D|R), p(D|NR) - probability that if a relevant (non-rel
document is retrieved, it is D.

30. p(D | R)p(R)
p(R | D) =
p(D)
p(D | NR)p(NR)
p(NR | D) =
p(D)
Ranking Principle (Bayes’ Decision Rule):
If p(R|D) > p(NR|D) then D is relevant,
Otherwise D is not relevant

31.  Bayes Decision Rule
 A document D is relevant if P(R|D) > P(NR|D)
 Estimating probabilities
 use Bayes Rule
 classify a document as relevant if
○ Left side is likelihood ratio

32.  Can we calculate P(D|R)? Probability that if a relevant
document is returned it is D?
 If we KNOW we have relevant set of documents (maybe
from humans?) We could calculate how often specific
words occur in a certain set.
 Ex: We have info on how often specific words occur in
relevant set. We could calculate how likely it is to see the
words appear in a set.
 Ex: Prob: “president” in the relevant set is 0.02 and
“lincoln” in the relevant set is “0.03”. If new doc. has
pres. & lincoln then prob. Is 0.02*0.03= .0006.

33.  Suppose we have a vector representing the presence and
absence of terms (1,0,0,1,1). Terms 1, 4, & 5 are present.
 What is the probability of this document occurring in the
relevant set?
 pi is the probability that the term i occurs in a relevant
set. (1- pi ) would be the probability a term would not be
included the relevant set.
 This gives us: p1 x (1-p2) x (1-p3) x p4 x p5

34.  Assume independence
 Binary independence model
 Dot product of over terms that have value
one. Zero means dot product over terms that
have value 0.
 pi is probability that term i occurs (i.e., has
value 1) in relevant document, si is
probability of occurrence in non-relevant
document

36.  Scoring function is (Last term was same
for all documents. So it can be ignored.

37.  Jump to machine learning and web
search. Lots of training data available
from web search queries. Learning to
rank models.
 http://www.bradblock.com/A_General_La
nguage_Model_for_Information_Retrieval
.pdf