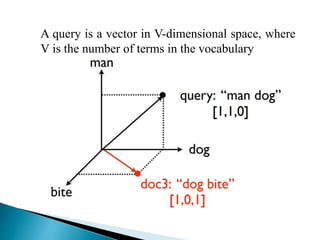
The document discusses various information retrieval models including Boolean, vector space, and probabilistic models. It provides details on how documents and queries are represented and compared in the vector space model. Specifically, it explains that in this model, documents and queries are represented as vectors of term weights in a multi-dimensional space. The similarity between a document and query vector is calculated using measures like the inner product or cosine similarity to retrieve and rank documents.

1. Ms. T. Primya
Assistant Professor
Department of Computer Science and Engineering
Dr. N. G. P. Institute of Technology
Coimbatore

2.  A retrieval model can be a description of either the
computational process or the human process of
retrieval
 the process of choosing documents for retrieval
 the process by which information needs are first
articulated and then refined.

3.  Boolean Models
 Vector Space Models
 Probabilistic Models
 Models based on Belief nets
 Models based on Language Models

4.  A document is represented as a set of keywords.
 Index terms are considered to be either present or absent in a
document and to provide equal evidence with respect to information
needs.
 Queries are Boolean expressions of keywords, connected by AND,
OR, and NOT, including the use of brackets to indicate scope.
[[Rio & Brazil] | [Hilo & Hawaii]] & hotel & !Hilton]
 Output: Document is relevant or not. No partial matches or ranking.

5.  User need: I’m interested in learning about vitamins
other than vitamin e that are anti-oxidants.
 User’s Boolean query: antioxidant AND vitamin
AND NOT vitamin e

6.  For each retrieval model, there explicit three
components:
 Document representation d
 Query q
 Ranking function R(d, q)

7.  An IR strategy is a technique by which a relevance
measure is obtained between a query and a document.
 Retrieve documents that make the query true.

8.  Boolean-Documents either match or don’t.
 Good for expert users with precise understanding of
their needs and of the collection.
 Also good for applications: Applications can easily
consume 1000s of results.
 Not good for the majority of users
 This is particularly true of web search.

9.  Boolean queries often have either too few or too many results.
Query 1
standard AND user AND dlink AND 650
→ 200,000 hits Feast!
Query 2
standard AND user AND dlink AND 650 AND no AND card AND found
→ 0 hits Famine!
 In Boolean retrieval, it takes a lot of skill to come up with a query that
produces a manageable number of hits.
 In ranked retrieval, “feast or famine” is less of a problem.
 Condition: Results that are more relevant are ranked higher than results that
are less relevant. (i.e., the ranking algorithm works.)

10.  A commonly used measure of overlap of two sets
 Let A and B be two sets
 Jaccard coefficient:
jaccard(A,B) = |A∩B| |A∪B|
 jaccard(A,A) = 1
 jaccard(A,B) = 0 if A∩B = 0
 A and B don’t have to be the same size. Always
assigns a number between 0 and 1.

11. What is the query-document match score that the Jaccard
coefficient computes for:
 Query
“ides of March”
 Document
“Caesar died in March”
jaccard(q,d) = 1/6

12.  It doesn’t consider term frequency (how many
occurrences a term has).
 Rare terms are more informative than frequent terms.
 Jaccard does not consider this information.

13. Advantages
 Can use very restrictive search
 Makes experienced users happy
 Clear formalism
 Simplicity
 It is still used in small scale searches like searching e-
mails, files from local hard drives

14. Disadvantages
 Simple queries do not work well.
 Complex query language, confusing to end users
 Difficult to control the number of documents
retrieved.
◦ All matched documents will be returned.
 Difficult to rank output.
◦ All matched documents logically satisfy the query.
 Difficult to perform relevance feedback.
◦ If a document is identified by the user as relevant or
irrelevant, how should the query be modified?

15.  Vector space model or term vector model is an
algebraic model for representing text documents (and
any objects, in general) as vectors of identifiers, such
as, for example, index terms.
 It is used in information filtering, information
retrieval, indexing and relevancy rankings.

16. The basis vectors correspond to the dimensions or
directions of the vector space

17. A vector is a point in a vector space and has length
(from the origin to the point) and direction

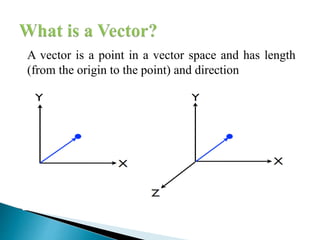
18.  A 2-dimensional vector can be written as [x, y]
 A 3-dimensional vector can be written as [x, y, z]

19.  Let V denote the size of the indexed vocabulary
 Any arbitrary span of text (i.e., a document, or a
query) can be represented as a vector in V-
dimensional space
 let’s assume three index terms: dog, bite, man (i.e.,
V=3)

20. 1 = the term appears at least once
0 = the term does not appear

21. A query is a vector in V-dimensional space, where
V is the number of terms in the vocabulary

22.  The vector space model ranks documents based on
the vector-space similarity between the query vector
and the document vector
 There are many ways to compute the similarity
between two vectors
 One way is to compute the inner product

23. Multiply corresponding components and then sum
of those products

24. Pros and Cons
 The inner-product doesn’t account for the fact that
documents have widely varying lengths
 All things being equal, longer documents are more
likely to have the query-terms
 So, the inner-product favours long documents

25.  Document represented as a vector:
d =< d1; d2; …. dn >
 Query represented as a vector: q =< q1; q2;…. qn >
 Ranking function (retrieval status value):

26.  The cosine similarity between two vectors (or two
documents on the Vector Space) is a measure that
calculates the cosine of the angle between them.
 the cosine similarity equation is to solve the equation
of the dot product for the :
 The numerator is the inner product
 The denominator is the product of the two vector-
lengths
 Ranges from 0 to 1 (equals 1 if the vectors are
identical)

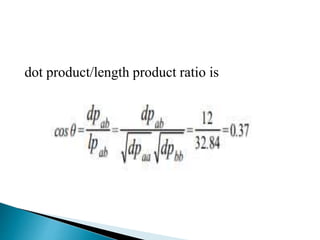
27.  a =[1, 2, 3]
 b =[4,-5,6]
a with b is dpab = 1*4 + 2*-5 + 3*6 = 12
a with itself is dpaa = 1*1 + 2*2 + 3*3 = 14
b with itself is dpbb = 4*4 + -5*-5 + 6*6 = 77
la = (dpaa) ½ = (14) ½ = 3.74; i.e., the length of a.
lb = (dpbb) ½ = (77)½ = 8.77; i.e., the length of b.
la*lb = (dpaa) ½ * (dpbb) ½ = 32.83;
i.e., the length product (lpab) of a and b.

28. dot product/length product ratio is

29.  The vector space model procedure can be divided
into three stages.
 The first stage is the document indexing where
content bearing terms are extracted from the
document text.
 The second stage is the weighting of the indexed
terms to enhance retrieval of document relevant to the
user.
 The last stage ranks the document with respect to the
query according to a similarity measure.