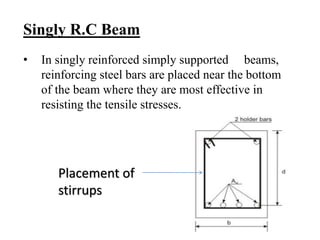
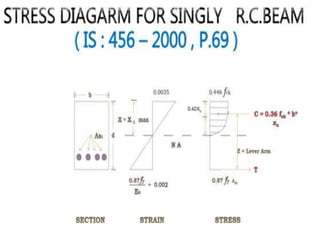
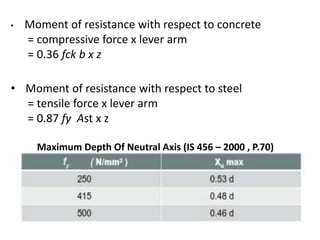
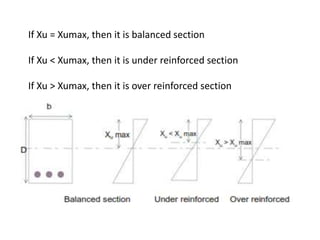
The document details the design and analysis of singly reinforced concrete beams according to IS 456:2000, focusing on the placement of reinforcing steel and the calculation of moments of resistance. It includes examples for analyzing and designing concrete sections with given dimensions and material properties, illustrating the required calculations for maximum compression stress, lever arm, tension, and compression. Additionally, the document outlines the method for determining the area of tension reinforcement and the number of bars required for a specific design moment.

1. Vishwakarma Government
Engineering College,
Chandkheda
Name:- Vekaria Darshil(150170106061)
Branch:- Civil
Sub:- Elementary Structural Design (ESD)
Sem:- 6th
Topic:- Singly Reinforced Concrete Beam
(R.C.C as per is IS: 456-2000)

2. • In singly reinforced simply supported beams,
reinforcing steel bars are placed near the bottom
of the beam where they are most effective in
resisting the tensile stresses.
Singly R.C Beam
Placement of
stirrups

4. • Xumax = Maxi. Depth of Neutral axis
• b = width of beam
• d = effective depth
• Z = d-0.42xu
= lever arm
• D = overall depth
• Xu = depth of N.A
• Ast = area of tension steel
• Resultant force of compression(C) = average stress X area
= 0.36(fck)(b)(Xu)
• Resultant force of tension (T) = 0.87(fy)(Ast)
• Force of compression should be equal to force of tension(C=T),
So, 0.36(fck)(b)(Xu) = 0.87(fy)(Ast)
hence, Xu = 0.87(fy)(Ast)
0.36(fck)(b)

5. • Moment of resistance with respect to concrete
= compressive force x lever arm
= 0.36 fck b x z
• Moment of resistance with respect to steel
= tensile force x lever arm
= 0.87 fy Ast x z
Maximum Depth Of Neutral Axis (IS 456 – 2000 , P.70)

6. If Xu = Xumax, then it is balanced section
If Xu < Xumax, then it is under reinforced section
If Xu > Xumax, then it is over reinforced section

7. Moment of resistance

8. Limiting value of tension steel
and moment of resistance
• Since the maximum depth of neutral axis is limited,
the maximum value of moment of resistance is also
limited.

9. Types of problems:-
1) Analysis of a section
2) Design of a section

10. 1) Analysis example:-
Q. For a limiting section 200 mm x 300 mm effective , determine the
following:
1) max. compression stress in concrete
2) lever arm
3) Total tension
4) Total compression
if it is reinforced with an effective cover of 50 mm. Take M-20 concrete and Fe
250 grade steel.
Solution :-
Given:-
b= 200mm
d= 300mm
fck= 20 N/mm2
The given section is balanced section,
Therefore, Xu=Xumax (IS 456-2000, Pg- 70)

11. For Fe-250 ,
Xu max = 0.53x 300 = 159mm
Xu = Xu max = 159mm
1) max. compression stress in concrete = 0.446x fck
=0.446x 20
= 8.92 N/mm2
2) Lever arm (Z) = d - 0.42Xu
= 233.22 mm
3) Total tension (T) = 0.87(fy)(Ast)
for Ast: for limiting section, Xu = Xu max,
Xu= 0.87(fy)(Ast)/ 0.36(fck)(b)
(from -IS 456-2000, Pg 96)
therefore , Ast = 1052.6 mm2

12. Total tension (T) = 0.87(fy)(Ast)
= 0.87 x 250 x 1052.6
= 228.96 kN
Total compression (C) = 0.36(fck)(b)(xu)
= 0.36 x 20 x 200 x 159
= 228.96 kN
For limiting section :- C =T
Hence verified.

13. 2) Design example:-
Q. 300mm x 500mm R.C.C beam section is subjected to a design
moment of 120 kN.m . Find the area of tension
reinforcement as per IS Code and no. of bars required. Take
effective cover 50mm, M20 concrete and steel Fe -415.
Solution :-
Given that , Mu = 120kN.m
To find Ast :
pt = 50 fck / fy ( 1- (1- 4.6 Mu / fck bd2)1/2
pt = 0.63%

14. We know,
Ast = pt bd /100
= 850.5 mm2
 Consider 20mm diameter bars
So, Ast = 3.14 x 20 x20
= 314.15 mm2
Therefore ,
 No. of bars = 850.5/314.15
= 2.71
say 3 Nos.
Ast provided = 3 x 314.15
= 942.45 mm2
Therefore , Provide 3 Nos- 20 mm dia. bars
(Ast = 942.45mm2)

15. THANK YOU