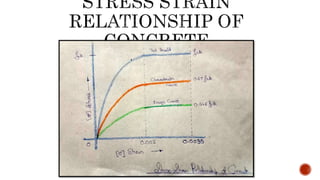
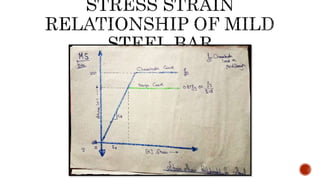
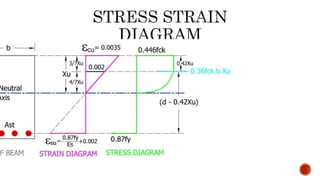
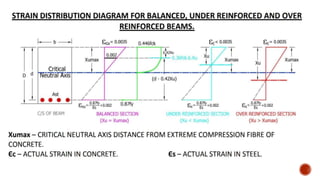
The document discusses the design of singly reinforced concrete beams. It provides assumptions and steps for calculating the ultimate moment of resistance of a beam. This includes calculating the neutral axis depth, comparing it to the maximum depth, and using the appropriate equation to find ultimate moment based on if the beam is under-reinforced or over-reinforced. Two example problems are then provided to demonstrate designing a beam to resist a given load and calculating its dimensions and reinforcement details.

1. Notion Educations

2.  It is the acceptable limits for safety and serviceability requirements for the structure
before its failure occurs.
 The design of structures by this method will thus ensure that they will not reach limit
states and will not become unfit for the use for which they are intended. It is worth
mentioning that structures will not just fail or collapse by violating (exceeding) the
limit states.
Assumptions:
 Plane sections normal to the axis remain plane after bending.
 The maximum strain in concrete at the outer most compression fiber is taken as 0.0035 in bending .
 The acceptable stress-strain curve of concrete is assumed to be parabolic.
 The tensile strength of concrete is ignored.
 The design stresses of the reinforcement are derived from the representative stress-strain curves .
 The maximum strain in the tension reinforcement in the section at failure shall not be less than Fy/(1.15 Es) + 0.002,
where fy is the characteristic strength of steel and Es = modulus of elasticity of steel

10.  Find out ultimate moment of resistance (Mu)
 Design a singly reinforced beam

11.  Step 1) calculate Xumax
 Step 2) Calculate actual N.A.
Xu = 0.87/0.36*Fy/Fck*Ast/b
 Step 3) Compare actual N.A.(Xu) with max N.A.(Xumax),
Xu=Xumax, then it is a balance section,
Xu<Xumax, then it is a under-reinforced section.
Xu>Xumax, then it is a over reinforced section.
 Step 4) calculate ultimate moment of resistance at
tension side,
Mu = 0.87Fy*Ast*(d-0.42Xu)
Compresion side
Mu=0.36fck*b*Xu*(d-0.42Xu)

12. Design of Singly reinforced Beam
Q : Q.1) Calculate the ultimate moment of resistance of the singly – reinforced section shown below.
Use M20 & Fe415 grade of concrete & steel.
=>
d=270 mm
b=230 mm
Step 1 : To calculate Xumax Step 3: to compare Xu with Xumax,
As Fe 415 is used Xu max=0.48d so, here Xu < Xumax, it is a under reinforced
section
Therefore, Xumax = 0.48*270=129.6 mm Step 4 : To find Mu
Mu=0.87fyAst(d-0.42Xu)
Step 2 : To calculate Xu = 0.87*415*(270-0.42*73.91)
Xu = 0.87 fy*Ast/0.36fck*b = 29.24 X 10^6 N/mm
= 0.87*415*339/0.36*20*230
= 73.91 mm
339
mm2

13. Design of Singly reinforced Beam
Q : Q.2)Design a rectangular RCC beam for a clear span of 5 m with 230 mm bearings subjected to
super imposed load of 25 kn/m. Use M20 concrete and Fe 415 steel.
Solution:
Step 1 : To find Effective span
Le = 5-0.230=4.77m
Step 2 : to find Factored Load
Wu=25*1.5=37.5Kn
Step 3: To find Ultimate moment of resistance (Mu)
Mu=Wu*Le*Le/8
= 106.65 KN-m
=106.65*10^6 N-mm
Step 4 : to find Effective depth (d)
d
d=395.79 mm =say 400mm
D= d + eff.cover= d+cover+ phi/2=
400+20+6=426mm
So, b=230 mm,d=400mm , D=
426mm
Step no 5: Calculate Ast
Ast
Ast = 750mm^2 approx
Provide 4 nos of 16mm dia bar