This document discusses stress diagrams and design considerations for singly reinforced concrete beams. It covers notation, stress conditions, types of failure, and formulas for moment of resistance. The key points are: 1) A stress diagram shows the compression and tension zones of a beam based on the depth of the neutral axis. The moment of resistance depends on the neutral axis location. 2) Beam sections can be balanced, under-reinforced, or over-reinforced depending on when concrete or steel yields. Under-reinforced sections are preferred. 3) Formulas are provided to calculate the moment of resistance based on the steel or concrete stresses for different section types. Reinforcement criteria specify minimum and maximum steel ratios.

1. PREPARED BY:
Asst. Prof. GAURANG PRAJAPATI
CIVIL DEPARTMENT
SINGLY R C BEAM
Mahatma Gandhi Institute Of
Technical Education
& Research Centre, Navsari (396450)
ELEMENTARY STRUCTURAL DESIGN
6TH SEMESTER
CIVIL ENGINEERING

2. STRESS DIAGRAM FOR SINGLY R. C. BEAM [IS 456, PAGE NO. 69]
ESD
2160607
2
SINGLY R C BEAM

3. STRESS DIAGRAM FOR SINGLY R. C. BEAM [IS 456, PAGE NO. 69]
 Notation of diagram:
ESD
2160607
3
SINGLY R C BEAM
b = Width of beam xu max. = Max. Depth of N.A.
d = Effective Depth of beam Z = Lever Arm = d – 0.42 xu
D = Overall depth of beam fck = Compressive Strength of Concrete
C.C. = Clear Cover fy = Yield Strength of Steel
Ast = Area of Steel C = Force of Compression (in Concrete)
= 0.36 fck b xu
xu = Depth of Neutral Axis (N.A.) T = Force of Tension (in Steel)
= 0.87 fy Ast

4. STRESS DIAGRAM FOR SINGLY R. C. BEAM [IS 456, PAGE NO. 69]
 Clear cover: The thickness of concrete from the surface of reinforcement bar to the
nearest edge of concrete is called Clear cover (Nominal cover)
 Effective cover: The thickness of concrete from the centre of reinforcement bar to the
nearest edge of concrete is Effective cover.
 Lever arm: The vertical distance between compression force and tension fore is called
Lever arm.
 Maximum stain at outermost fibers in compression and tension in a Singly R C Beam
under limit state of collapse by flexure:
o Maximum stain at outermost fibres in compression = 0.0035
o Maximum stain at outermost fibres in tension =
𝑓𝑦
1.15 𝐸 𝑠
+ 0.002
o Max. Compressive stress in concrete = 0.446 fck
o Max. Tensile stress in steel = 0.87 fy
ESD
2160607
4
SINGLY R C BEAM

5. NEUTRAL AXIS [N.A.]
• The Axis which separate compression zone and tension zone in the cross section of
a beam is known as “Neutral Axis.”
• For simply supported beam, the c/s above N.A. is in compression, while the cross
section below N.A. is in Tension.
• C = Compression force in Concrete
= 0.36 fck b xu
• T = Tension Force in Steel
= 0.87 fy Ast
But, C = T
0.36 fck b xu = 0.87 fy Ast
ESD
2160607
5
SINGLY R C BEAM
xu =
𝟎.𝟖𝟕 𝒇 𝒚 𝑨 𝒔𝒕
𝟎.𝟑𝟔 𝒇 𝒄𝒌 𝒃
IS 456
Clause No.: G-1.1 (a)
Page No.: 96

6. MAX. DEPTH OF NEUTRAL AXIS [N.A.]
 The failure of beam may be due to the failure of concrete or failure of steel.
 Failure due to concrete is called brittle failure, while failure due to steel is called ductile
failure.
 When amount of steel in beam is more than that required for balanced condition, the
neutral axis moves towards bottom for balancing.
 Therefore tensile stress in steel reaches its ultimate value, before maximum compressive
stress is reached in concrete, and steel will fail by yielding. Thus, the brittle failure of
concrete can be avoided.
 Therefore, the depth of neutral axis up to which brittle failure (compressive failure) of
concrete can be avoided is known as maximum depth of neutral axis (xu max.).
 To avoid brittle failure, xu ≯ xu max. Therefore, a good designer ensures ultimate failure by first
yielding of steel in tension followed by compression failure of concrete.
ESD
2160607
6
SINGLY R C BEAM

7. TYPES OF BEAM SECTIONS:
1. Balanced section
2. Under Reinforced section (U.R.S.)
3. Over Reinforced section (O.R.S.)
ESD
2160607
7
SINGLY R C BEAM

8. TYPES OF BEAM SECTIONS:
1. Balanced Section (Limiting Section)
• Compressive strain in concrete and Tensile strain in steel reaches their limiting
strain values simultaneously.
• Both the materials steel and concrete will fail at the same time.
• xu = xu max., Mu = Mu lim., Pt = Pt lim.
• Moment of Resistance (Mu)can be calculated w.r.t. steel or concrete.
• Mu = C × Z or Mu = T × Z
ESD
2160607
8
SINGLY R C BEAM
Mu lim. = 0.36
𝒙 𝒖 𝒎𝒂𝒙.
𝒅
(1 – 0.42
𝒙 𝒖 𝒎𝒂𝒙.
𝒅
) fck b d2 IS 456
Clause No.: G-1.1 (c)
Page No.: 96

9. TYPES OF BEAM SECTIONS:
2. Under Reinforced section
• Tensile strain in steel reaches limiting strain
0.87 𝑓𝑦
𝐸𝑠
+ 0.002, earlier to compressive
strain in concrete reaching the limiting value of 0.0035.
• So, steel will fail before concrete. Steel is a ductile material and yields before
failure.
• Such failure is called tension failure or ductile failure.
• As steel is ductile material, it gives sufficient warning before failure, hence the
under reinforced sections are preferred by designers.
• xu < xu max., Mu < Mu lim., Pt < Pt lim.
ESD
2160607
9
SINGLY R C BEAM

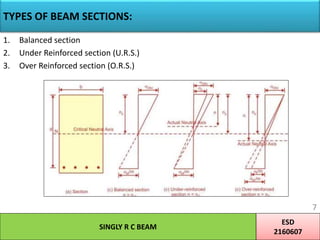
10. TYPES OF BEAM SECTIONS:
 Moment of Resistance (Mu) w.r.t. Steel (For Under Reinforced Section)
Mu = T × Z
= 0.87 fy Ast × [d – (0.42 xu)]
= 0.87 fy Ast × [d – (0.42
0.87 𝑓𝑦 𝐴 𝑠𝑡
0.36 𝑓 𝑐𝑘 𝑏
)]
= 0.87 fy Ast × [d –
𝑓𝑦 𝐴 𝑠𝑡
𝑓 𝑐𝑘 𝑏
]
ESD
2160607
10
SINGLY R C BEAM
Mu = 0.87 fy Ast d [1 –
𝒇 𝒚 𝑨 𝒔𝒕
𝒇 𝒄𝒌 𝒃 𝒅
]
IS 456
Clause No.: G-1.1 (b)
Page No.: 96

11. TYPES OF BEAM SECTIONS:
3. Over Reinforced section
• R.C. sections in which the limiting strain in concrete (0.0035) is reached earlier than
the yield strain of steel (
0.87 𝑓𝑦
𝐸𝑠
+ 0.002), are called over reinforced section. (O.R.S)
• At failure steel is not yet yielded and concrete burss out.
• As the concrete is brittle material, the failure is brittle and sudden.
• As there is no warning of failure in such sections, IS code recommends avoiding
such designs.
• xu > xu max., Mu > Mu lim., Pt > Pt lim.
ESD
2160607
11
SINGLY R C BEAM

12. TYPES OF BEAM SECTIONS:
 Moment of Resistance (Mu) w.r.t. Concrete
(For Balanced & Over Reinforced Section)
Mu = C × Z
= 0.36 fck b xu (d – 0.42 xu)
= 0.36 fck b xu d(1 – 0.42
𝑥 𝑢
𝑑
)
= 0.36 fck b
𝑥 𝑢
𝑑
d2(1 – 0.42
𝑥 𝑢
𝑑
)
= 0.36
𝑥 𝑢
𝑑
(1 – 0.42
𝑥 𝑢
𝑑
) fck b d2
Take xu = xu max. for & Mu = Mu lim.
ESD
2160607
12
SINGLY R C BEAM
Mu lim. = 0.36
𝒙 𝒖 𝒎𝒂𝒙.
𝒅
(1 – 0.42
𝒙 𝒖 𝒎𝒂𝒙.
𝒅
) fck b d2 IS 456
Clause No.: G-1.1 (c)
Page No.: 96

13. MOMENT OF RESISTANCE (MU)
ESD
2160607
13
SINGLY R C BEAM

14. REINFORCEMENT CRITERIA
ESD
2160607
14
SINGLY R C BEAM
𝐀 𝐒
𝐛𝐝
=
𝟎.𝟖𝟓
𝐟 𝐲
IS 456
Clause No.: 26.5.1.1 (b)
Page No.: 46, 47
 Minimum area of reinforcement for a beam in tension
 Maximum area of reinforcement for a beam in tension
Ast = 0.04 b D IS 456
Clause No.: 26.5.1.1 (b)
Page No.: 47
i.e. 4% of cross section area of beam