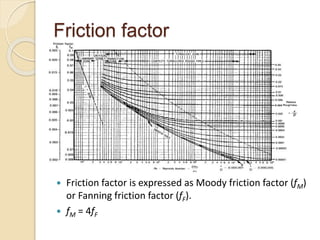
The document provides guidelines for pipe sizing in single-phase fluid flow, including definitions, calculations, and methodologies to determine pressure drop in pipes and fittings. It discusses Bernoulli’s equation, friction factors, and standard practices for calculating fluid velocity and pipe pressure drops using various methods. Additionally, references to essential literature are included for further reading on the topic.

1. Single-phase fluid flow
GUIDELINE TO PIPE SIZING FOR SINGLE-PHASE FLOW
AUTHOR: VIKRAM SHARMA
DATE: 7th MARCH 2017

2. Table of Contents
 Introduction
 Bernoulli’s Equation
 Friction factor graph
 Pressure Drop in Pipe and Fittings
 Recommended fluid velocities
 Calculation Methodology
 References

3. Introduction
 Pipe is a common sight in chemical plant
 Pipework & fittings:
◦ ≈ 20-30% of the total design cost;
◦ ≈ 10-20% of the total plant investment; and
◦ Other added cost due to maintenance req. & energy usage
in the form of ΔP in the fluids being pumped
 The size of a pipe (diameter) is expressed in two
ways that are:
◦ Nominal Pipe Size (NPS); and
◦ Diametre Nominal (DN)
 NPS is measured in inches, DN is measured in mm
 DN is generally equiv. to NPS multiplied by 25

4. Introduction (cont’d)
 DN is generally equiv. to NPS multiplied by 25
except:
◦ NPS ½ is DN15
◦ NPS 3 is DN80
 Pipe size are designated by two numbers that are
(i) pipe diameter and (ii) thickness
 Pipe diameter is generally associated with inside
dia.
 Outside dia. is the same for a given size →
maintain certain interchangeability of pipe fittings
 NPS 14 and beyond, it is equal to the outside dia.
(OD) in inch.

5. Introduction (cont’d)
 NPS 14 and beyond, it is equal to the outside dia.
(OD) in inch. (cont’d)
 Pipe wall thickness is referred to pipe schedule
(Sch)
 Standardize from 5 to 160 → determined by the
service req. like Pressure, Temp., Flow and
corrosion
 Pipe wall thickness ↑ Pipe Schedule ↑

6. Bernoulli’s Equation
 ΔP or head loss in a piping system is caused by:
◦ Elevation;
◦ Friction;
◦ Shaft work; and
◦ Turbulence due to sudden change in direction or cross
sectional area
 Mechanical Energy Balance (MEB) eq.→ conservation of sum
of pressure, kinetic and potential energies, net heat transfer
(q), work done by the system (w) and frictional energy (ef).
 ef is usually +ve & represents the rate of irreversible
conversion of mech. energy into thermal energy
 Sometimes called head loss, friction loss or frictional
pressure drop.

7. Bernoulli’s Equation (cont’d)

8. Bernoulli’s Equation (cont’d)
 The first 3 terms (pressure, velocity & elevation) are
point functions → depend only on conditions at the
inlet & outlet of the system
 w and ef are path functions → depend on what is
happening to the system between the inlet and outlet
points
 ef loss due to friction and includes losses due to flow
through lengths of pipe, fittings such as elbows, valves,
orifices and pipe entrances and exits

9. Bernoulli’s Equation (cont’d)
 Kf is the excess head loss due to pipe or pipe fittings, v is
the fluid velocity
 Fluids flowing through pipes;
 ΔP is the same due to flow is the same whether the
pipe is horizontal, vertical or inclined

10. Friction factor
 Friction factor is expressed as Moody friction factor (fM)
or Fanning friction factor (fF).
 fM = 4fF

11. Friction factor (cont’d)
 Laminar region (or viscous): Re < 2,000
 “Critical zone” is the transition frm. laminar to
turbulent: 2,000 < Re < 4,000.
 Turbulent flow: Re > 4,000
 Friction factor is laminar region is not affected by the
relative roughness (ε/D) but it is influenced by the fluid
viscosity
 Friction factor at transition region strongly depends on
both the Re and ε/D
 Friction factor at turbulent region is independent of Re
and is a function of relative roughness (ε/D).

12. Friction factor (cont’d)
 Friction factor can be computed using two equations
based on the fluid flow regime.
 Laminar flow (Re < 2,000) :
 Turbulent flow (Re > 4,000):
 Reynolds Number: 𝜌∙𝑣∙𝐷
𝜇
◦ fD = Darcy friction factor
◦ ε = Absolute pipe roughness (m):
 Carbon Steel = 0.02-0.05 mm
 Stainless steel = 0.03 mm
◦ D = Pipe inner diameter (m)
◦ ρ = Fluid density (kg/m3)
◦ µ = Dynamic viscosity (Ns/m2)

13. Friction factor (cont’d)
 Colebrook’s equation require iteration to determine the
friction factor.
 Author propose Churchill (1977) equation that allows
engineers to determine the friction factor for both
laminar and turbulent flows.

14. Pressure Drop in Pipe and
Fittings
 ΔP for straight pipe run: ∆𝑃𝑏𝑎𝑟/100𝑚=
0.5∙𝑓 𝐷∙𝜌∙𝑣2
𝐷
 Pressure drop for fittings can be computed using
resistance coefficient method (K).
 This could be done via Darby 3-K method for fittings
 Why Darby 3-K method is preferred?
◦ Accounts directly for the effect of both Re & fitting size on the
loss coefficient.

15. Pressure Drop in Pipe and
Fittings (cont’d)
 Other option: The Equivalent Length Method (Leq/D)
 The Leq/D method assumes that:
◦ Size of fittings of a given type can be scaled corresponding to a given dia.
◦ Reynolds number on the friction loss is the same as the pipe loss
 The above assumptions are incorrect. Why?
 The laminar or turbulent flow within a valve or a fitting
is generally quite different from that of straight pipe.
 With this, there is an uncertainty when determining the
effect of Re on the loss coefficients.
 Leq/D method does not account for the lack of exact
scaling for valves and fittings

16. Pressure Drop in Pipe and
Fittings (cont’d)
 For Darby 3-K constants, refer to:
◦ https://neutrium.net/fluid_flow/pressure-loss-from-fittings-
3k-method/
 For other fittings such as sudden pipe contractions,
square reduction, tapered reduction, sharp orifice,
square expansion, tapered expansion, thick orifice
and pipe reduce, refer to Coker (2007)

17. Recommended fluid
velocities
 Typical velocities and pressure drop:
◦ Liquid (pumped, not viscous): 1-3 m/s, 0.5 kPa/m
◦ Liquid (gravity flow): - m/s , 0.05 kPa/m
◦ Gases & vapours: 15-30 m/s, 0.02 % of the line pressure
◦ HP steam (> 8 bar): 30-60 m/s, - kPa/m
 Typical velocities at pump suction and discharge
lines:

18. Recommended fluid velocities
(cont’d)
 Typical velocities and pressure drop for single-
phase gas process lines:

19. Calculation Methodology
 Obtain the piping layout from PFD, P&IDs or Piping
Isometrics
 Obtain data at fluid inlet of the pipe corresponding to
inlet temperature and pressure. Info req. are mass flow,
ρ, µ, T & P.
 Select a pipe size and material (Refer to Slide #5)
 Calc. the fluid velocity. Ensure it comply with the fluid
req. (Refer to Slide #17)
 Calc. Re → Laminar or Turbulent (Refer to Slide #12)
 Calc. the fD → Churchill’s (1977) eq. (Refer to Slide #13)
 Calc. the ΔPbar/100m of the straight pipe. Include elevation
(Refer to Slide #14).
 Calc. ΔPbar by multiplying with pipe straight length

20. Calculation Methodology
(cont’d)
 Calc. ΔP of fittings. Use Darby 3-K method and
Coker (2007) (Refer to Slide #16 and Slide #14)
 Calc. ΔP of other items such as process equipment
etc.
 Calc. the total pressure drop of the system (ΣP)
◦ ΣPT = ΔPfriction + ΔPfittings + ΔPother items
 Check if downstream pressure P2 is as per
specifications.
◦ P2 = P1 - ΣPT
 If not, repeat the above calc. by selecting a
different pipe size

21. References
 Bahadori, A. (2014). Process pipe sizing for plants
location. In Natural Gas Processing: Technology and
Engineering Design (p. 83). Oxford: Gulf Professional
Publishing.
 Murty, K. K. (2010). Sizes, Schedules, And Standards.
In All-in-One Manual of Industrial Piping Practice and
Maintenance On-The-Job Solutions, Tips and Insights
(p. 52). New York: Industrial Press.
 Native Dynamics. (2012, May 19). Neutrium. Retrieved
March 7, 2017, from Absolute Roughness of Pipe
Material: https://neutrium.net/fluid_flow/absolute-
roughness/
 Sinnot, R. K. (2005). Piping and Instrumentation. In
Chemical Engineering Design (Vol. 6, p. 218). Oxford:
Elsevier.