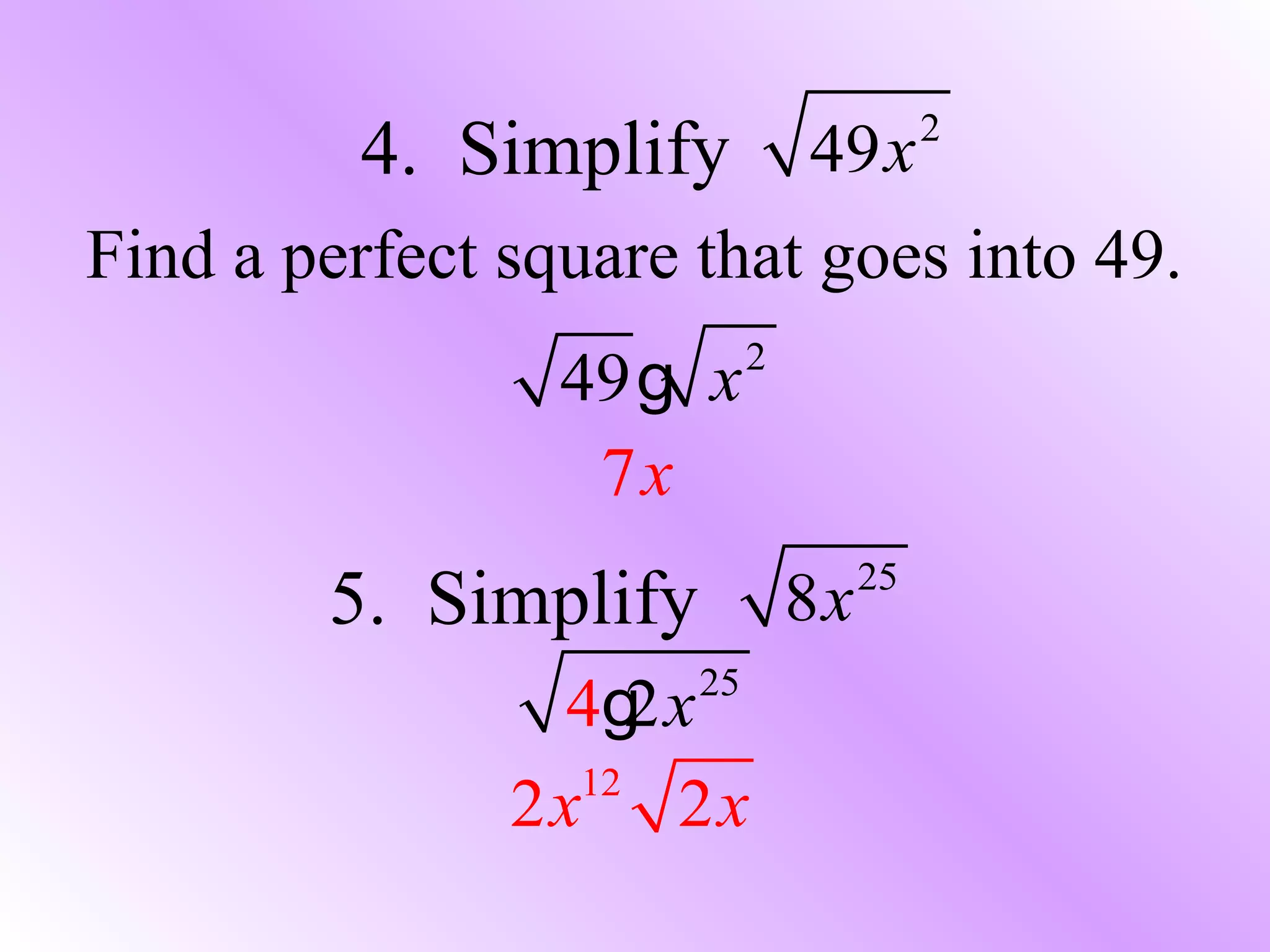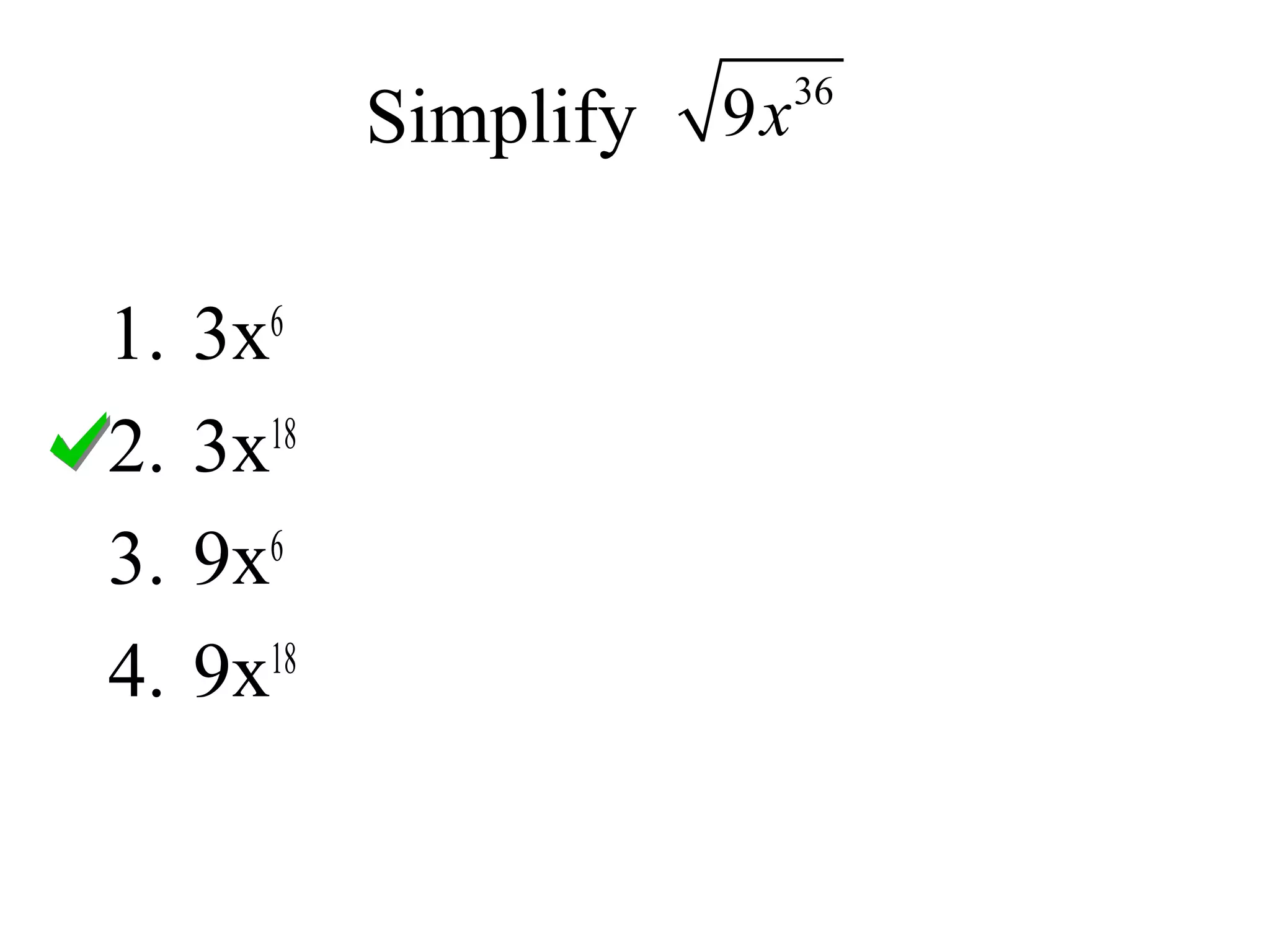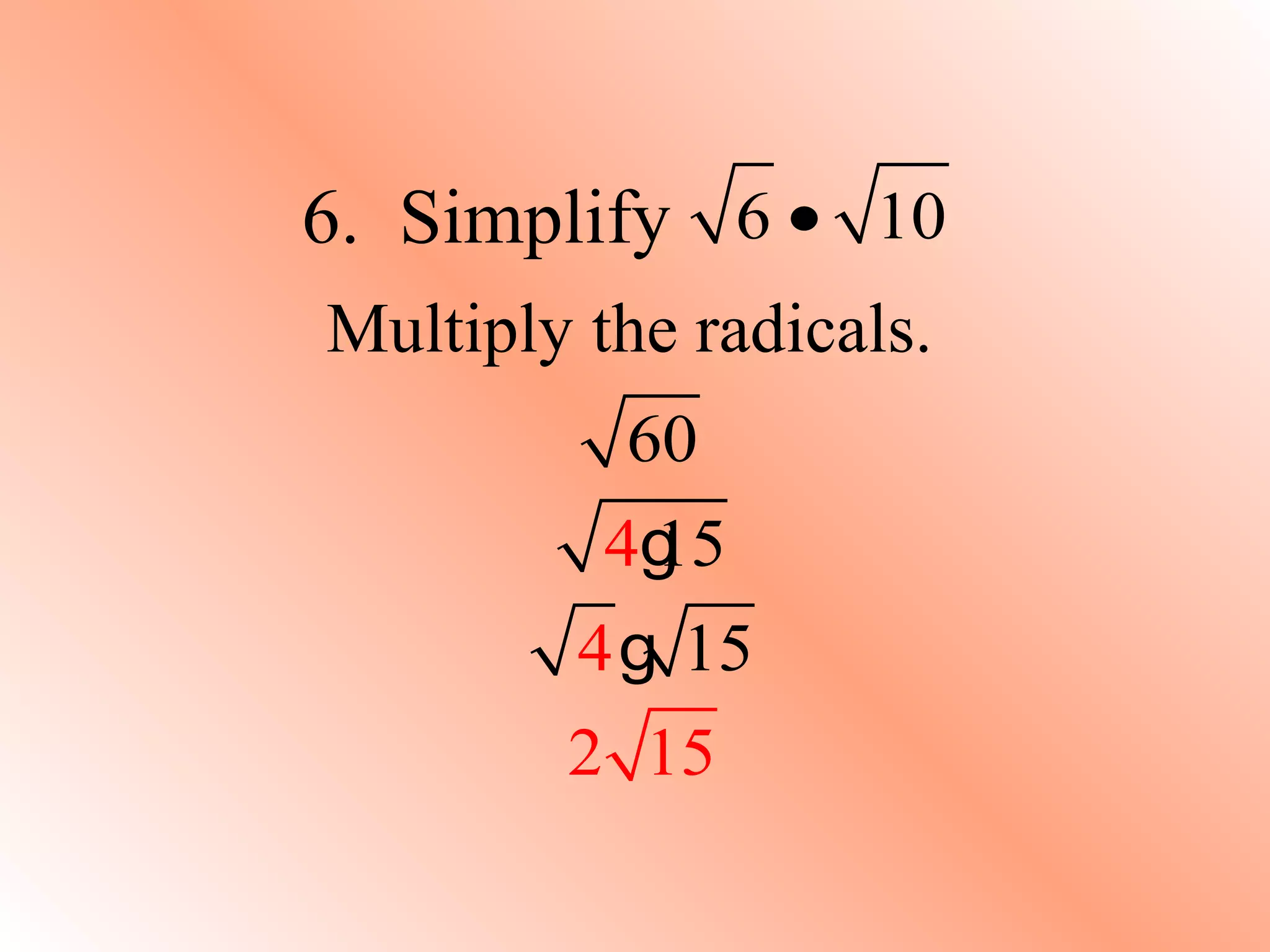This document provides objectives and instructions for simplifying square roots and radical expressions. It begins by defining the radical sign and radicand. Examples are then provided to simplify square roots of various numbers. The document continues with examples of simplifying variables within radicals by dividing the exponent by two. It also discusses identifying when a radical problem is fully simplified by having no radicals in the denominator or fractions within radicals.

1. Objectives
The student will be able to:
1. simplify square roots, and
2. simplify radical expressions.

2. In the expression ,
is the radical sign and
64 is the radicand.
If x2
= y then x is a square root of y.
1. Find the square root:
8
2. Find the square root:
-0.2
64
64
− 0.04

3. 11, -11
4. Find the square root:
21
5. Find the square root:
3. Find the square root: ± 121
441
−
25
81
5
9
−

4. 6.82, -6.82
6. Use a calculator to find each
square root. Round the decimal
answer to the nearest hundredth.
± 46.5

5. 1 • 1 = 1
2 • 2 = 4
3 • 3 = 9
4 • 4 = 16
5 • 5 = 25
6 • 6 = 36
49, 64, 81, 100, 121, 144, ...
What numbers are perfect squares?

6. 1. Simplify
Find a perfect square that goes into 147.
147
147 349= g
147 349= g
147 7 3=

7. 2. Simplify
Find a perfect square that goes into 605.
605
121 5g
121 5g
11 5

8. Simplify
1. .
2. .
3. .
4. .
2 18
72
3 8
6 2
36 2

9. Look at these examples and try to find the pattern…
How do you simplify variables in the radical?
x7
1
x x=
2
x x=
3
x x x=
4 2
x x=
5 2
x x x=
6 3
x x=
What is the answer to ?x7
7 3
x x x=
As a general rule, divide the
exponent by two. The
remainder stays in the
radical.

10. Find a perfect square that goes into 49.
4. Simplify 49x2
2
49 xg
7x
5. Simplify 25
8x
25
4 2xg
12
2 2x x

11. Simplify 36
9x
1. 3x6
2. 3x18
3. 9x6
4. 9x18

12. Multiply the radicals.
6. Simplify 6 • 10
60
4 15g
4 15g
2 15

13. 7. Simplify 2 14 •3 21
Multiply the coefficients and radicals.
6 294
6 49 6g
6 649g g
42 6
6 67g g

14. Simplify
1. .
2. .
3. .
4. .
2
4 3x
4
4 3x
2
48x
4
48x
3
6 8x xg

15. How do you know when a radical
problem is done?
1. No radicals can be simplified.
Example:
2. There are no fractions in the radical.
Example:
3. There are no radicals in the denominator.
Example:
8
1
4
1
5

16. 8. Simplify.
Divide the radicals.
108
3
108
3
36
6
Uh oh…
There is a
radical in the
denominator!
Whew! It
simplified!

17. 9. Simplify 8 2
2 8
4 1
4
4
2
2
Uh oh…
Another
radical in the
denominator!
Whew! It simplified
again! I hope they
all are like this!

18. 10. Simplify
5
7
5
7
75
7 7
= g
35
49
=
35
7
=
Since the fraction doesn’t reduce, split the radical up.
Uh oh…
There is a
fraction in
the radical!
How do I get rid
of the radical in
the denominator?
Multiply by the “fancy one”
to make the denominator a
perfect square!