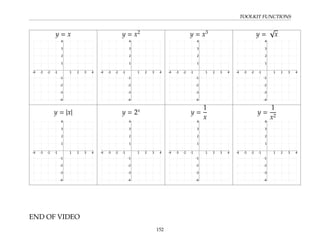
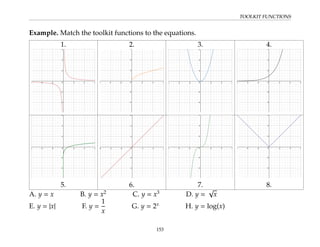
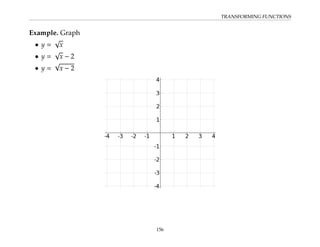
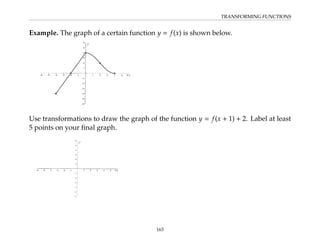
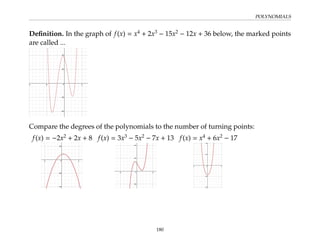
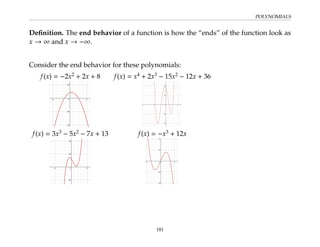
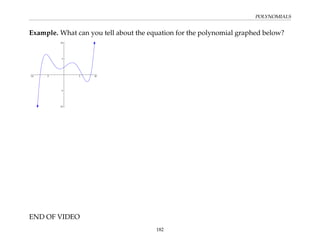
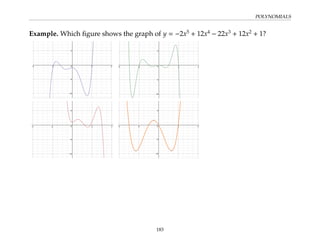
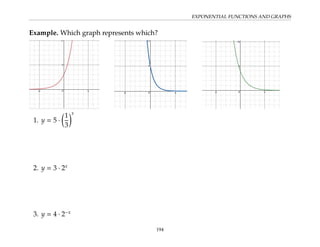
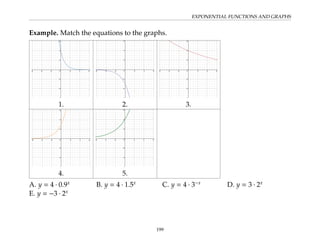
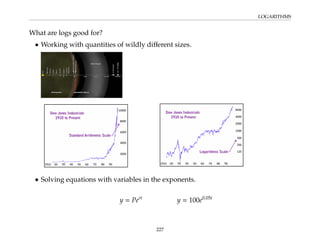
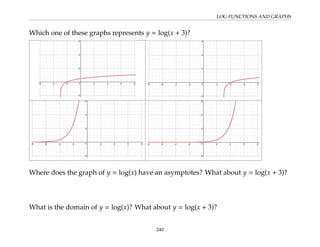
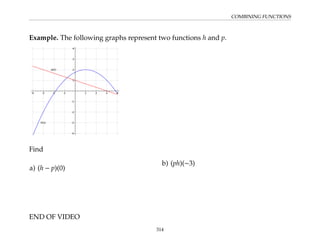
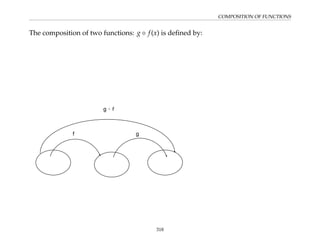
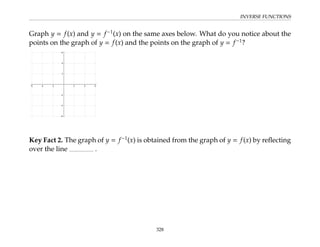
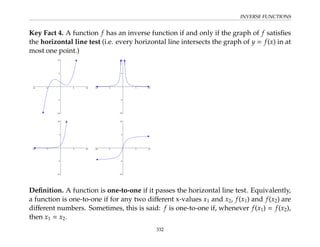
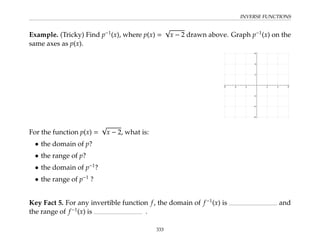
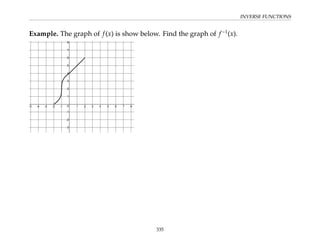
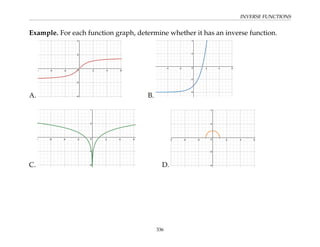
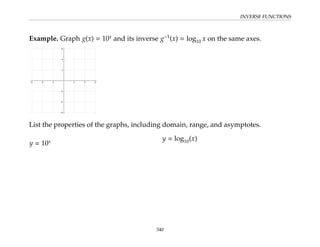
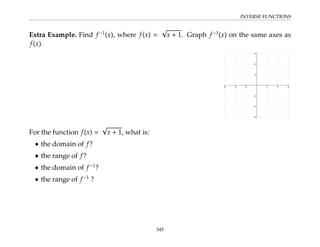
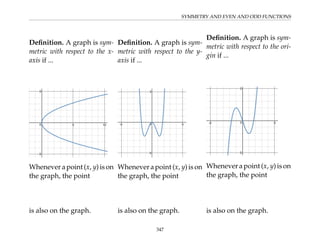
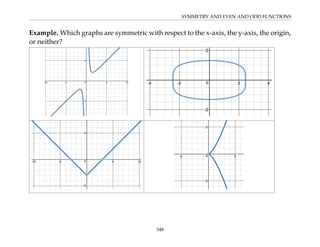
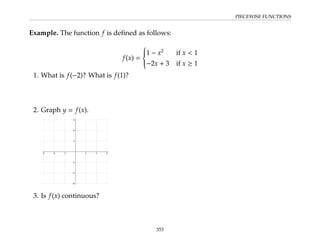
This document provides an overview of the Math 110 Algebra - Fall 2018 course. It covers exponents, radicals, factoring, rational expressions, solving quadratic equations, solving rational equations, and solving radical equations. The course aims to teach students various rules and techniques for simplifying expressions and solving equations involving these algebraic concepts. Examples are provided to demonstrate each technique, along with practice problems for students to test their understanding.
































































































![COMPOUND LINEAR INEQUALITIES
Example. Which of the following expressions are equivalent to: ”x ≤ 1 OR x 3”
(select all that apply)
A. 1 ≥ x 3
B. 3 x ≤ 1
C. [1, 3)
D. (−∞, 1] ∪ (3, ∞)
E. x ≤ 1 AND x 3
99](https://image.slidesharecdn.com/classnotesm1102018f-221120020829-aa1628c3/85/classNotes_m110_2018F-pdf-99-320.jpg)





![POLYNOMIAL AND RATIONAL INEQUALITIES
Example. The solution to (x + 2)(x + 1) ≤ 0 is
A. (−∞, −1]
B. (−∞, −2]
C. [−2, ∞)
D. [−2, −1]
E. (−∞, −2] ∪ [−1, ∞)
105](https://image.slidesharecdn.com/classnotesm1102018f-221120020829-aa1628c3/85/classNotes_m110_2018F-pdf-105-320.jpg)



































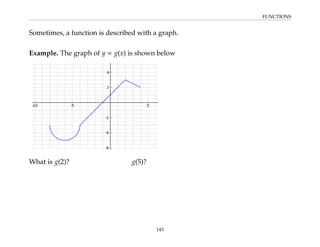
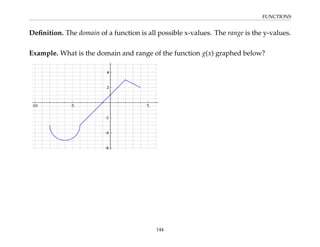


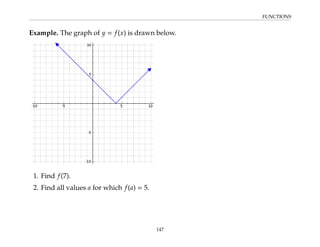


![FUNCTIONS
Example. Find the domain of g(x) =
√
3 − x
x + 1
A. (−∞, 3)
B. (−∞, 3]
C. (−1, 3]
D. (−∞, −1) ∪ (−1, 3)
E. (−∞, −1) ∪ (−1, 3]
150](https://image.slidesharecdn.com/classnotesm1102018f-221120020829-aa1628c3/85/classNotes_m110_2018F-pdf-150-320.jpg)