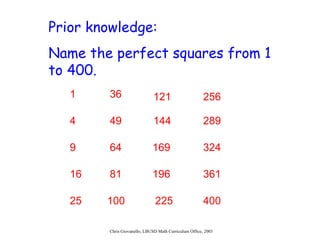
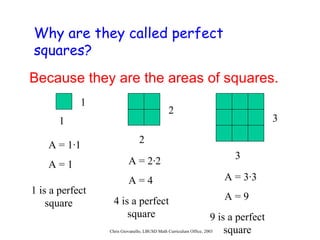
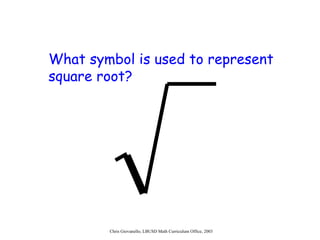
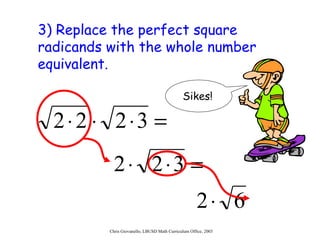
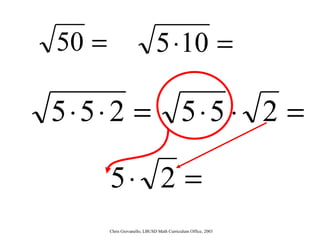The document provides instructions for students on how to simplify radicals. It defines what it means to simplify a radical as having no perfect square factors in the radicand. The objective is for students to be able to simplify at least 9 out of 10 radicals correctly. Students are taught to rewrite the radicand using prime factorization, replace any perfect square factors with their numeric equivalent, and check if the radicand is simplified by having no remaining perfect square factors. Examples are worked through and students complete guided practice problems to demonstrate their understanding.

1. Radicals are rad!

2. I wonder if they can be simplified? Hmmmmm….

3. “ Simplified” means that there are no perfect square factors in the radicand.

4. Objective: Given 10 different radicals, students will be able to simplify at least 9 of them correctly.

5. Purpose: To be able to compute radicals and express the answer in simplest radical form To do well on their assessments quizzes chapter test final exam CRCT Yeah! Way cool!

6. Prior knowledge: Name the perfect squares from 1 to 400. 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400

7. Why are they called perfect squares? Because they are the areas of squares. 1 1 2 2 3 3 A = 1·1 A = 1 A = 2·2 A = 4 A = 3·3 A = 9 1 is a perfect square 4 is a perfect square 9 is a perfect square

8. Is 8 a perfect square? No o o o o o !

9. What symbol is used to represent square root?

10. Name the parts: radical, radical sign,or square root sign

11. Name the parts: radicand

12. Simplify the following: 11 15 7 17

13. What if the radicand is not a perfect square? Huh?

14. 1) Rewrite the radicand using prime factorization. That’s easy!

15. 2) Use the following theorem: Why separate here? Because

16. 3) Replace the perfect square radicands with the whole number equivalent. Sikes!

17. Is Simplified? Yes! Because the radicand has no perfect square factors.

18. That was way easy! Give me another one to work out. Simplify:

20. Check for Understanding: Thumbs up or Thumbs down To simplify a radical, first rewrite the radicand into prime factorization. Why?

21. Guided practice: Simplify the following radicals. Fold a paper into fourths. Number each section from 1 to 4. Put the answer to each question in each of the sections. (Fill the section.) On the count of 3, show me the answer to #1. On the count of 3, show me the answer to #2. On the count of 3, show me the answer to #3. On the count of 3, show me the answer to #4.

22. You are now ready to add and subtract radicals!