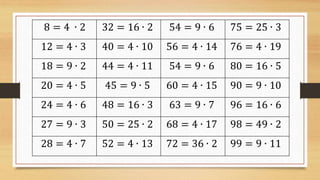
This document outlines the process of solving quadratic equations by extracting square roots, aimed at Grade 9 mathematics students. It presents the conditions under which quadratic equations have real solutions based on the value of k and demonstrates extraction of square roots through several examples. The document also includes various calculations and solutions, providing a comprehensive guide on handling quadratic equations.

1. Grade 9 – Mathematics
Quarter I
SOLVING QUADRATIC EQUATIONS BY
EXTRACTING SQUARE ROOTS

2. Objectives:
1. familiarize numbers that are
perfect squares; and
2. solve quadratic equations by
extracting square roots.

4. Quadratic Equations that can be written in the form 𝒙𝟐 = 𝒌 can be solved
by applying the following properties:
1. If 𝑘 > 0, then 𝒙𝟐 = 𝒌 has two real solutions or roots: 𝑥 = ± 𝑘.
2. If 𝑘 = 0, then 𝒙𝟐 = 𝒌 has two real solutions or roots: 𝑥 = 0
3. If 𝑘 < 0, then 𝒙𝟐 = 𝒌 has no solutions or roots:
Speaking Mathematically
𝑥 = ± 36 is read as ‘𝒙 is equal to the positive or negative square root of 36’
𝑥 − 5 2is read as “the square root of the square of the quantity 𝒙 𝒎𝒊𝒏𝒖𝒔 𝟓".

5. 𝑥2 = 49
𝑥2 = ± 49
𝑥 = ± 7
How to extract square roots?

6. 𝑥2 = 169
𝑥2 = ± 169
𝑥 = ± 13
How to extract square roots?

7. 8 = 4 ∙ 2 32 = 16 ∙ 2 54 = 9 ∙ 6 75 = 25 ∙ 3
12 = 4 ∙ 3 40 = 4 ∙ 10 56 = 4 ∙ 14 76 = 4 ∙ 19
18 = 9 ∙ 2 44 = 4 ∙ 11 54 = 9 ∙ 6 80 = 16 ∙ 5
20 = 4 ∙ 5 45 = 9 ∙ 5 60 = 4 ∙ 15 90 = 9 ∙ 10
24 = 4 ∙ 6 48 = 16 ∙ 3 63 = 9 ∙ 7 96 = 16 ∙ 6
27 = 9 ∙ 3 50 = 25 ∙ 2 68 = 4 ∙ 17 98 = 49 ∙ 2
28 = 4 ∙ 7 52 = 4 ∙ 13 72 = 36 ∙ 2 99 = 9 ∙ 11

8. 8 = 4 ∙ 2 54 = 9 ∙ 6
12 = 4 ∙ 3 56 = 4 ∙ 14
18 = 9 ∙ 2 54 = 9 ∙ 6
20 = 4 ∙ 5 60 = 4 ∙ 15
24 = 4 ∙ 6 63 = 9 ∙ 7
27 = 9 ∙ 3 68 = 4 ∙ 17
28 = 4 ∙ 7 72 = 36 ∙ 2
32 = 16 ∙ 2 75 = 25 ∙ 3
40 = 4 ∙ 10 76 = 4 ∙ 19
44 = 4 ∙ 11 80 = 16 ∙ 5
45 = 9 ∙ 5 90 = 9 ∙ 10
48 = 16 ∙ 3 96 = 16 ∙ 6
50 = 25 ∙ 2 98 = 49 ∙ 2
52 = 4 ∙ 13 99 = 9 ∙ 11
𝑥2 = 75
Get the square root of both sides
Factor the perfect squares
Get the square root of the
perfect square.
𝑥2 = 75
𝑥 = ± 25 ∙ 3
𝑥 = ± 25 3
𝑥 = ± 5 3

9. 𝟐 𝒙 − 𝟓 𝟐 = 𝟑𝟐
Divide both sides by 2
Get the square root of both sides
𝒙 − 𝟓 𝟐 = 𝟏𝟔
𝒙 − 𝟓 𝟐 = 𝟏𝟔
𝒙 − 𝟓 = ± 𝟒
𝒙 − 𝟓 = −𝟒
𝒙 = −𝟒 + 𝟓
𝒙 = 𝟏
Find the solutions or roots.
𝒙 − 𝟓 = 𝟒
𝒙 = 𝟒 + 𝟓
𝒙 = 𝟗
𝟐 𝒙 − 𝟓 𝟐 = 𝟑𝟐
𝟐

10. 𝟑 𝟒𝒙 − 𝟏 𝟐 − 𝟏 = 𝟏𝟏
Divide both sides by 3 𝟑 𝟒𝒙 − 𝟏 𝟐 = 𝟏𝟐
𝟒𝒙 − 𝟏 𝟐 = 𝟒
𝟒𝒙 − 𝟏 = 𝟐
4𝒙 = 𝟑
𝟑
𝒙 =
𝟒
𝟒𝒙 − 𝟏 = −𝟐
4𝒙 = −𝟏
𝒙 =
−𝟏
𝟒
Get the square root of both sides
Find the solutions or roots.
𝟒𝒙 − 𝟏 𝟐 = 𝟒
𝟒𝒙 − 𝟏 = ± 𝟐
𝟑 𝟒𝒙 − 𝟏 𝟐 = 𝟏𝟐
𝟑

11. 𝟐𝒙 − 𝟑 𝟐 = 𝟏𝟖
Get the square root of both sides
2𝑥 − 3 2 = 18
2𝑥 − 3 2 = ± 9 ∙ 2
2𝑥 − 3 = ± 9 2
2𝑥 − 3 = ±3 2
2𝑥 − 3 = ±3 2
𝟐𝒙 − 𝟑 = 𝟑 𝟐
𝟐𝒙 = 𝟑 + 𝟑 𝟐
𝒙 =
𝟑 + 𝟑 𝟐
𝟐
𝟐𝒙 − 𝟑 = −𝟑 𝟐
𝟐𝒙 = 𝟑 − 𝟑 𝟐
𝒙 =
𝟑 − 𝟑 𝟐
𝟐

12. 𝟐 𝟓𝒙 + 𝟐 𝟐 = 𝟔𝟒
5𝑥 + 2 2 = 32
5𝑥 + 2 2 = ± 16 ∙ 2
2
5𝑥 + 2 = ± 16
5𝑥 + 2 = ±4 2
𝒙 =
Divide both sides by 2
5𝑥 + 2 2 = 32
Get the square root of both sides
5𝑥 + 2 = ± 4 2
𝟓𝒙 + 𝟐 = 𝟒 𝟐 𝟓𝒙 + 𝟐 = − 𝟒 𝟐
𝟓𝒙 = −𝟐 + 𝟒 𝟐 𝟓𝒙 = −𝟐 − 𝟒 𝟐
𝒙 =
−𝟐 + 𝟒 𝟐 −𝟐 − 𝟒 𝟐
𝟓 𝟓
𝟐 𝟓𝒙 + 𝟐 𝟐 = 𝟔𝟒
𝟐