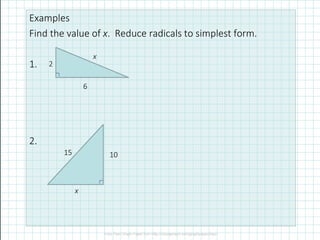
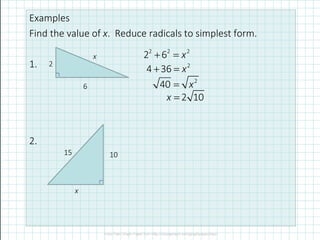
The document discusses simplifying radicals (square roots). It provides steps to simplify a radical: find prime factors, group pairs that can be pulled out of the radical, and leave unpaired factors inside. An example simplifies the square root of 24 to 2√3. It also discusses multiplying radicals by multiplying the numbers outside and inside the radical signs, and squaring a radical removes the radical sign.

1. Simplifying Radicals
The student is able to (I can):
• Simplify a square root
• Multiply square roots

2. Square Roots
• When we are taking the square root of a number, we will
not always get a whole number answer.
• If your answer is not a whole number, then the number
your calculator gives you is a decimal approximationapproximationapproximationapproximation. This
is an irrational number, like π, which goes on forever.
• If I ask for an exact answerexact answerexact answerexact answer, I do notnotnotnot want a decimal – I
want you to leave it as a simplified radicalsimplified radicalsimplified radicalsimplified radical.

3. To simplify a radical (square root):
• Find all the prime factors of the number
• Group pairs of factors – these can be pulled out of the
radical
• Any factors that cannot be paired up must stay inside the
radical
Example: Simplify 24
24
2 12

4. To simplify a radical (square root):
• Find all the prime factors of the number
• Group pairs of factors – these can be pulled out of the
radical
• Any factors that cannot be paired up must stay inside the
radical
Example: Simplify 24
24
2 12
2 6
2 3

5. To simplify a radical (square root):
• Find all the prime factors of the number
• Group pairs of factors – these can be pulled out of the
radical
• Any factors that cannot be paired up must stay inside the
radical
Example: Simplify 24
24
2 12
2 6
2 3

6. To simplify a radical (square root):
• Find all the prime factors of the number
• Group pairs of factors – these can be pulled out of the
radical
• Any factors that cannot be paired up must stay inside the
radical
Example: Simplify 24
24
2 12
2 6
2222 3333
=i2 2 3 2 6

7. Examples
Find the value of x. Reduce radicals to simplest form.
1.
2.
2
6
x
15 10
x

8. Examples
Find the value of x. Reduce radicals to simplest form.
1.
2.
2 2 2
2 6 x+ =
2
4 36 x+ =
2
40 x=
2 10x =
2
6
x
15 10
x

9. Examples
Find the value of x. Reduce radicals to simplest form.
1.
2.
2 2 2
2 6 x+ =
2
4 36 x+ =
2
40 x=
2 10x =
2 2 2
10 15x + =
2
100 225x + =
2
6
x
15 10
x
2
125x =
125x =
5 5=

10. When you multiply radicals, you multiply the numbers on the
outside, then multiply the numbers on the inside, and
simplify if necessary.
Example: Multiply ( )( )3 3 2 6
( )( )
( )( )
3 2 6
3 6 18 3 2
=
= =
( )( ) ( )( ) 23 3 2 6 6 3 82 1= =

11. Sometimes in problems, you will be asked to square a square
root.
Example: Evaluate
• Square the outside term:
• Squaring a square root removes the square root, so
• Multiply.
( )
2
5 3
2
5 25=
( )
2
3 3=
( )( )25 3 75=