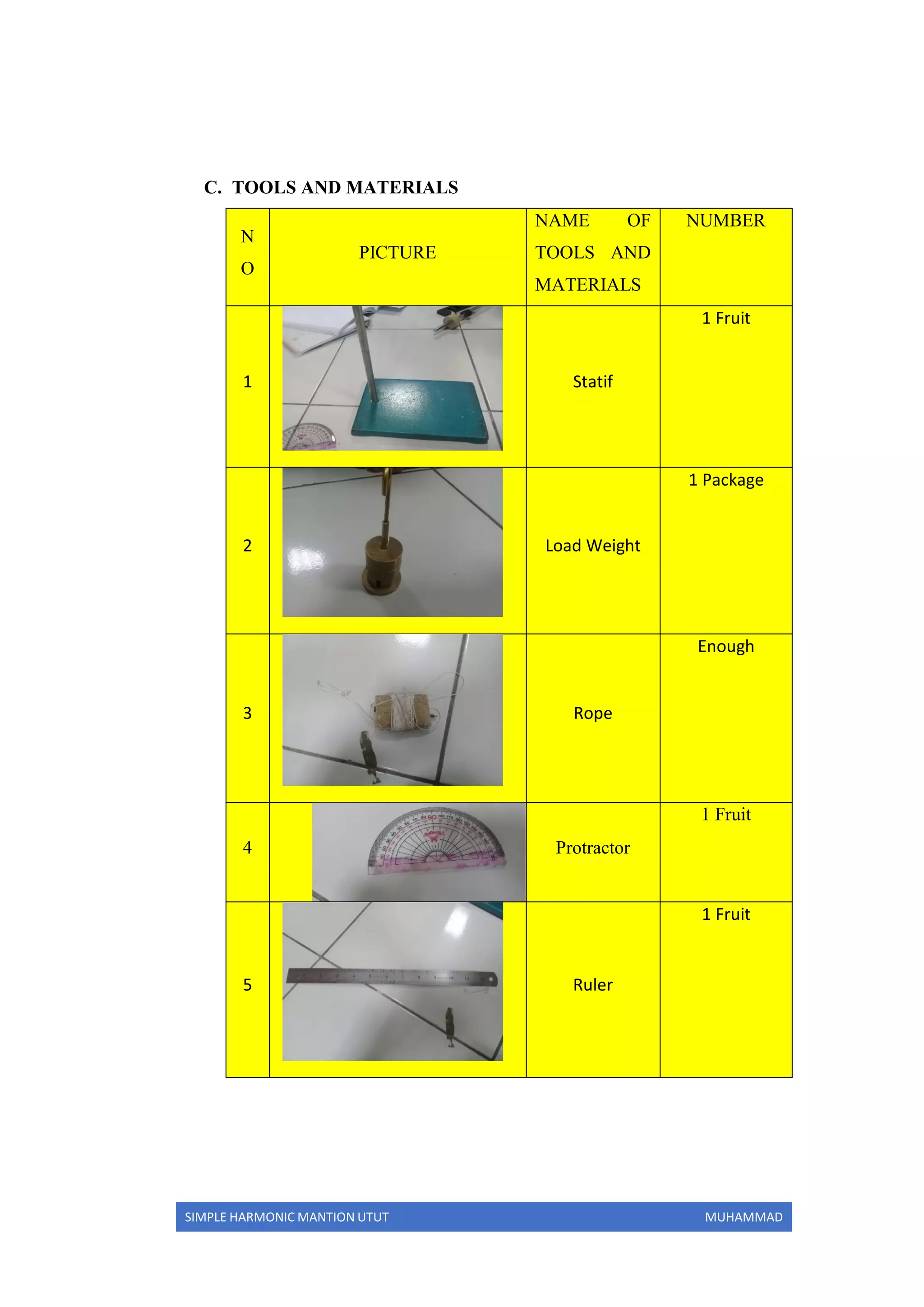
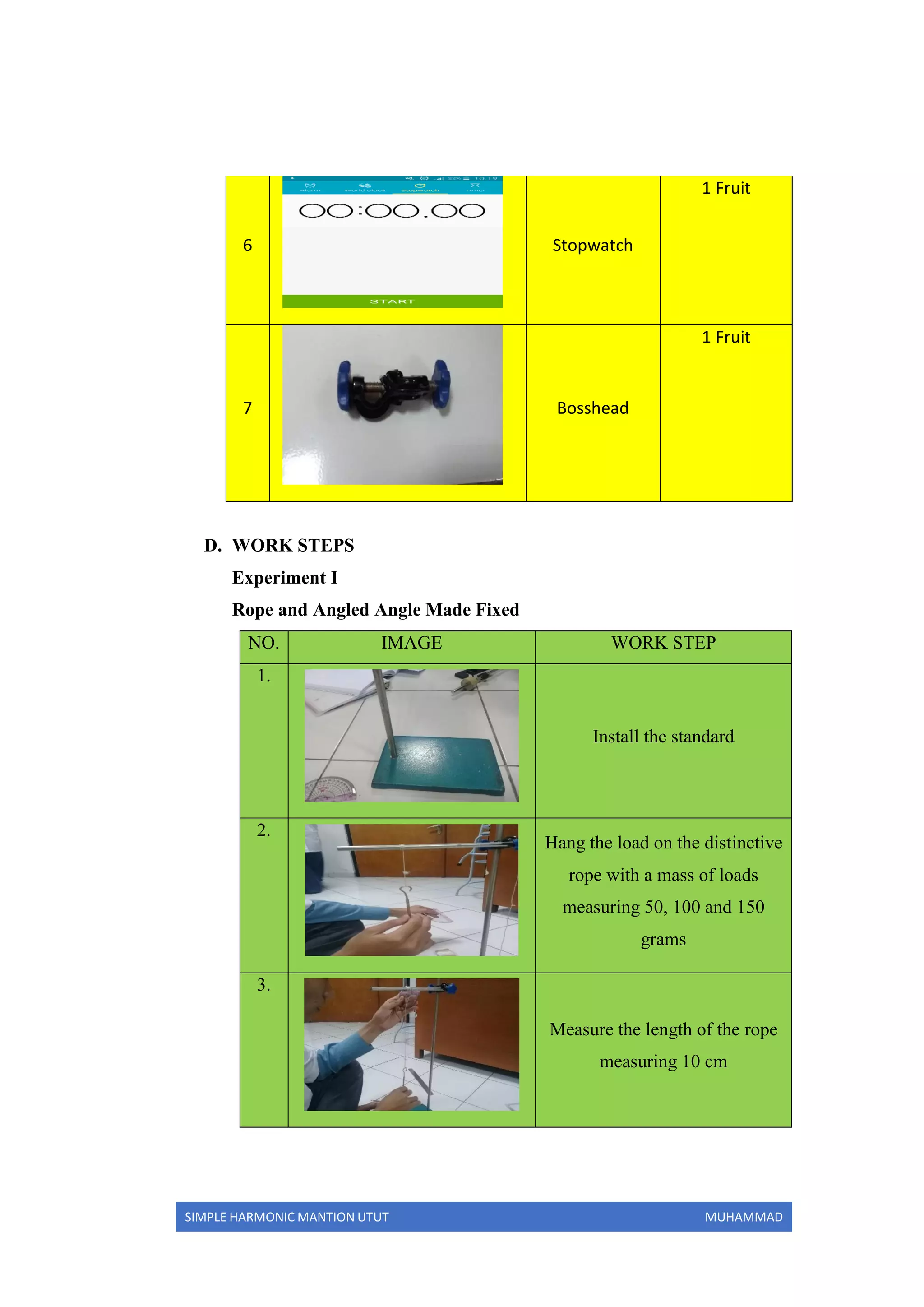
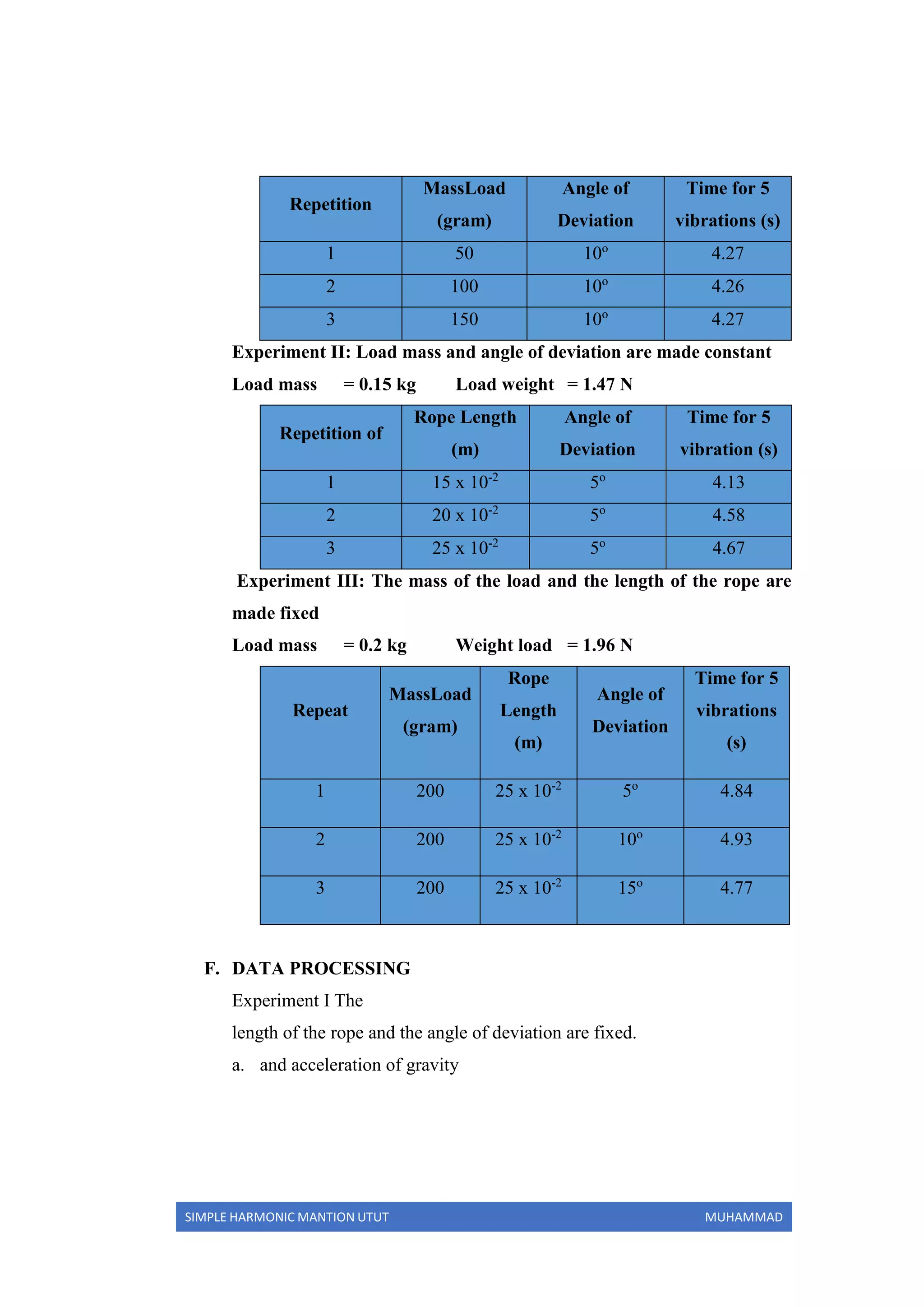
The document reports on an experiment to study simple harmonic motion using a simple pendulum. It describes the objectives of determining factors that affect gravity, measuring the pendulum's period, and understanding simple harmonic motion. The experiment varied the pendulum's mass, rope length, and angle of deviation to measure the period. The results were used to calculate the gravitational acceleration, which had a relative error of approximately 40-45% compared to the theoretical value. Increasing the rope length resulted in longer periods and gravitational values closer to theory.






![SIMPLE HARMONIC MANTION UTUT MUHAMMAD
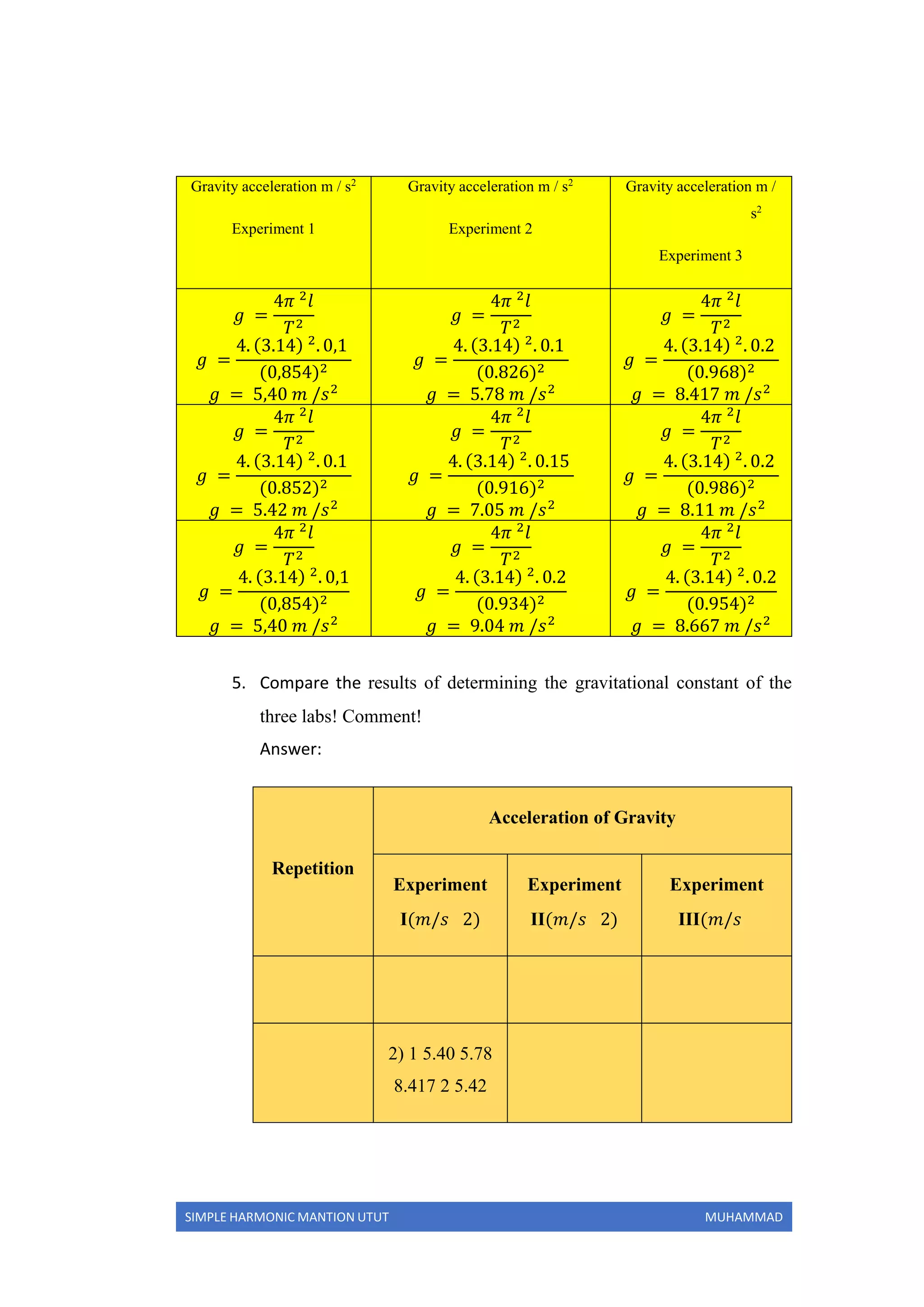
Repeat
Pendulum
periodPendulum
Period
Gravity Acceleration
1
𝑇 =
𝑡
𝑛
𝑇 =
4.27
5
𝑇 = 0.854 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.1 𝑚
0.8542
𝑔 = 5.40 𝑚 /𝑠2
2
𝑇 =
𝑡
𝑛
𝑇 =
4.25
5
𝑇 = 0.852 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.1 𝑚
0.8522
𝑔 = 5.42 𝑚 /𝑠2
3
𝑇 =
𝑡
𝑛
𝑇 =
4.27
5
𝑇 = 0.854 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.1 𝑚
0.8542
𝑔 = 5.40 𝑚 /𝑠2
b. Relative error
Repetition Relative error
1
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9.80665 𝑡𝑜 5.40
9.80665
] 𝑥 100%
𝐾𝑅 = [0.449]𝑥 100%
= 44.9% 𝐾𝑅
2
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9.80665 𝑡𝑜 5.40
9.80665
] 𝑥 100%
𝐾𝑅 = [0,447]𝑥 100%
= 44.7% 𝐾𝑅
3
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9.80665 𝑡𝑜 5.40
9.80665
] 𝑥 100%
𝐾𝑅 = [0.449]𝑥 100%
= 44.9% 𝐾𝑅
Experiment II](https://image.slidesharecdn.com/simpleharmonicmovementinbandul-190612114608/75/Simple-harmonic-movement-in-bandul-10-2048.jpg)
![SIMPLE HARMONIC MANTION UTUT MUHAMMAD
Massa load and angle deviation is made Equipment.
a. Pendulum period and gravitational acceleration.
Repetition of PendulumPeriod Gravity Acceleration
1
𝑇 =
𝑡
𝑛
𝑇 =
4.13
5
𝑇 = 0.826 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.1 𝑚
0.8262
𝑔 = 5.78 𝑚 /𝑠2
2
𝑇 =
𝑡
𝑛
𝑇 =
4.58
5
𝑇 = 0.916 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.15 𝑚
0.9162
𝑔 = 7.05 𝑚 /𝑠2
3
𝑇 =
𝑡
𝑛
𝑇 =
4.67
5
𝑇 = 0.934 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.2 𝑚
0.9342
𝑔 = 9.04 𝑚 /𝑠2
b. relative error
Repeatability Relative error
1
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9.80665 𝑡𝑜 5.78
9.80665
] 𝑥 100%
𝐾𝑅 = [0.410]𝑥 100%
= 41% 𝐾𝑅
2
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9,80665 − 7,05
9,80665
] 𝑥 100%
𝐾𝑅 = [0,281]𝑥 100%
𝐾𝑅 = 28,1%
3
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9, 80665 − 9.04
9,80665
] 𝑥 100%
𝐾𝑅 = [0.078]𝑥 100%
𝐾𝑅 = 7.8%
Experiment III
Rope length and load mass made Fixed](https://image.slidesharecdn.com/simpleharmonicmovementinbandul-190612114608/75/Simple-harmonic-movement-in-bandul-11-2048.jpg)
![SIMPLE HARMONIC MANTION UTUT MUHAMMAD
a. pendulum period and gravitational acceleration
Repeat Pendulum Period Gravity Acceleration
1
𝑇 =
𝑡
𝑛
𝑇 =
4 , 84
5
𝑇 = 0.968 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.2 𝑚
0.9682
𝑔 = 8.417 𝑚 /𝑠2
2
𝑇 =
𝑡
𝑛
𝑇 =
4.93
5
𝑇 = 0.986 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.2 𝑚
0.9862
𝑔 = 8.11 𝑚 /𝑠2
3
𝑇 =
𝑡
𝑛
𝑇 =
4.77
5
𝑇 = 0.954 𝑠
𝑔 =
4𝜋 2
𝑙
𝑇2
𝑔 =
4. (3.14) 2
. 0.2 𝑚
0.9542
𝑔 = 8.667 𝑚 /𝑠2
b. Relative error
Repetition Relative error
1
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9.80665 𝑡𝑜 8.417
9.80665
] 𝑥 100%
𝐾𝑅 = [0.1417]𝑥 100%
𝐾𝑅 = 14, 17%
2
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9,80665 − 8,11
9,80665
] 𝑥 100%
𝐾𝑅 = [0.173]𝑥 100%
𝐾𝑅 = 17.3%
3
𝐾𝑅 = [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅 = [
9,80665 − 8,667
9,80665
] 𝑥 100%
𝐾𝑅 = [0.116]𝑥 100%
𝐾𝑅 = 11.6%
G. DISCUSSION](https://image.slidesharecdn.com/simpleharmonicmovementinbandul-190612114608/75/Simple-harmonic-movement-in-bandul-12-2048.jpg)




![SIMPLE HARMONIC MANTION UTUT MUHAMMAD
, 40 9.04 8,667
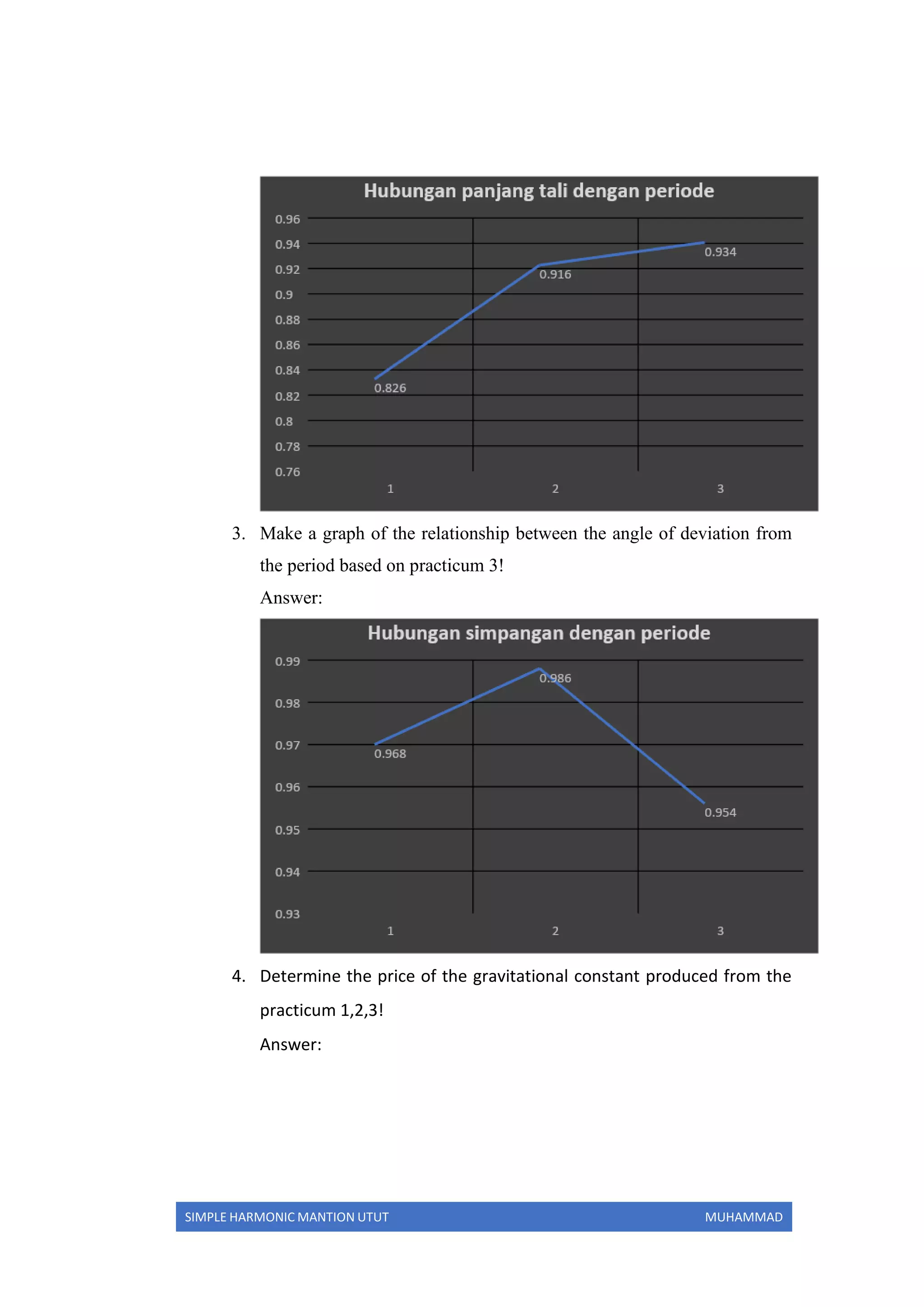
My opinion is a comparison with the experimental data above is
the second data on the third repetition that is equal to 9.04 𝑚 /𝑠2
and the
third data with the last data repetition that is equal to 8.667 𝑚 /𝑠2
.
Different from the first experiment, the data obtained is getting smaller
and the distance is getting farther away with the actual gravity value of
9.8 𝑚 /𝑠2
.
6. Determine the percentage of errors from the results of the calculation of
the three labs! If the gravitational acceleration is 9.80665 𝑚 /𝑠2
.
Answer:
ErrorRelative
Experiment 1
Error Relative
Experiment 2
Mistakes Relative
Experiment 3
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 5.4
9.80665
] 𝑥 100%
𝐾𝑅 = [0.449]𝑥 100%
𝐾𝑅 = 44 , 9%
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 5.78
9.80665
] 𝑥 100%
𝐾𝑅 = [0.41]𝑥 100%
= 41% 𝐾𝑅
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9,80665 − 8,417
9,80665
] 𝑥 100%
𝐾𝑅 = [0.1417]𝑥 100%
𝐾𝑅 = 14.17%
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9,80665 − 5 , 42
9.80665
] 𝑥 100%
𝐾𝑅 = [0,447]𝑥 100%
= 44.7% 𝐾𝑅
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 7.05
9.80665
] 𝑥 100%
𝐾𝑅 = [0.281]𝑥 100%
= 28.1% 𝐾𝑅
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 8.11
9.80665
] 𝑥 100%
𝐾𝑅 = [0.175]𝑥 100%
= 17.5% 𝐾𝑅
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 5.40
9.80665
] 𝑥 100%
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 9.04
9.80665
] 𝑥 100%
𝐾𝑅
= [
𝑔𝑡ℎ𝑒𝑜𝑟𝑦 − 𝑔 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑒𝑠
𝑔𝑡ℎ𝑒𝑜𝑟𝑦
] 𝑥 100%
𝐾𝑅
= [
9.80665 𝑡𝑜 8.667
9.80665
] 𝑥 100 %](https://image.slidesharecdn.com/simpleharmonicmovementinbandul-190612114608/75/Simple-harmonic-movement-in-bandul-19-2048.jpg)
![SIMPLE HARMONIC MANTION UTUT MUHAMMAD
𝐾𝑅 = [0.449]𝑥 100%
= 44.9% 𝐾𝑅
𝐾𝑅 = [0.078]𝑥 100%
= 7.8% 𝐾𝑅
𝐾𝑅 = [0.116]𝑥 100%
𝐾𝑅 = 11 , 6%
7. Which method do you think is closer to the real result? Explain your
argument!
Answer:
In my opinion, if you look at the comparison between the first to third
experiments, the closest to the theoretical gravitational acceleration is
9,80665 𝑚 /𝑠2,
which is the third experiment because the greatest
acceleration value of the experiment is 9.04 𝑚 /𝑠2
. In contrast to the
first experiment and the third data that is still far from the difference
with the gravitational acceleration theoretically, but in the third data it
is only less small to equate the theoretical gravitational perceptions, but
the second data with the third data approximation can be close to the
gravitational acceleration. So, actually because the mass of the load and
the amount of deviation does not affect the acceleration of gravity, it is
better to change the length of the rope, because the length of the rope
affects the acceleration of gravity, so we can compare the magnitude of
the acceleration according to the second experiment. .
8. Analyze the location of errors when practicing!
Answer:
When making a pendulum that is used to measure the time through a
stopwatch is the observer's inaccuracy when making a deviation and
stopping and starting the stopwatch, then on the string installation
statif by changing the string variable allows the error in the length of
the rope to be fixed at the pendulum installation. And also First, when
the measurement of the length of the rope may be wrong in the
measurement or when the practicum of the rope is used loosely from
the bond and change the length of the rope. Second, when measuring
the magnitude of the deviation from the pendulum each repetition
may differ slightly. Third, when the pendulum oscillates, the](https://image.slidesharecdn.com/simpleharmonicmovementinbandul-190612114608/75/Simple-harmonic-movement-in-bandul-20-2048.jpg)

