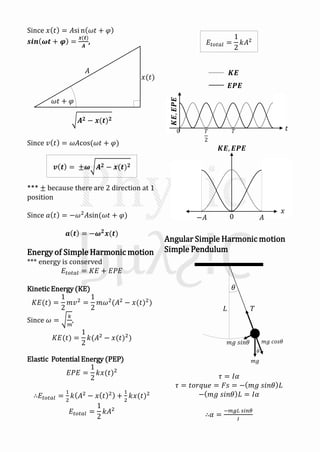
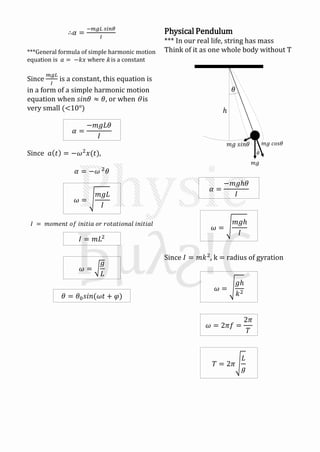
This document summarizes oscillatory motion and simple harmonic motion. It describes how oscillatory motion involves periodic movement like that of a mass-spring system without friction. The motion of such a system can be modeled using Newton's second law, resulting in a differential equation of the form d2x/dt2 = -kx, where k is a constant. This has the form of a simple harmonic motion equation. Other examples of simple harmonic motion discussed include angular simple harmonic motion using a simple pendulum, as well as damped simple harmonic motion where a frictional force is present. Key characteristics of simple harmonic motion like amplitude, angular velocity, phase constant, and the sinusoidal nature of the position, velocity and acceleration functions are also

![Oscillatory Motion
; periodic movement
Simple Harmonic motion
E.g.; mass-spring system (no friction)
2nd Newton law
𝐹 = 𝑚𝑎
At (a); 𝐹 = −𝑘 𝑠𝑝𝑟𝑖𝑛𝑔 𝑥 = 𝑚𝑎
Since 𝑎 =
𝑑2 𝑥
𝑑𝑡2,
−𝑘 𝑠𝑝𝑟𝑖𝑛𝑔 𝑥 = 𝑚
𝑑2
𝑥
𝑑𝑡2
𝑑2
𝑥
𝑑𝑡2
= −
𝑘 𝑠𝑝𝑟𝑖𝑛𝑔
𝑚
𝑥
Let
𝑘 𝑠𝑝𝑟𝑖𝑛𝑔
𝑚
be 𝜔2
,
𝑑2
𝑥
𝑑𝑡2
= −𝜔2
𝑥
m
m
m
(𝑎)
(𝑏)
(𝑐)
𝑥
-𝑥
𝑥 = 0
𝐹𝑠
𝐹𝑠
Math
Differential equation
𝑑𝑦
𝑑𝑥
= 𝑥2
𝑦
𝑑𝑦
𝑦
= 𝑥2
𝑑𝑥
𝑑𝑦
𝑦
= 𝑥2
𝑑𝑥
𝑙𝑛 𝑦 =
𝑥3
3
+ 𝑐
Homogeneous Second Order Linear
Differential Equations (2nd ODE)
𝑃 𝑥 𝑦′′
+ 𝑄 𝑥 𝑦′
+ 𝑅 𝑥 𝑦 = 𝐺(𝑥)
With constant coefficient
𝑎𝑦′′
+ 𝑏𝑦′
+ 𝑐𝑦 = 0
Change the form
𝑎𝑟2
+ 𝑏𝑟 + 𝑐 = 0
1. If there are 2 distinct roots, 𝑟1, 𝑟2
𝑦 = 𝑐1 𝑒 𝑟1 𝑥
+ 𝑐2 𝑒 𝑟2 𝑥
2. If there are a repeated single root, (𝑟)
𝑦 = 𝑐1 𝑒 𝑟𝑥
+ 𝑐2 𝑥𝑒 𝑟𝑥
3. If there are complex roots, (𝛼 ± 𝛽𝑗)
𝑦 = 𝑒 𝛼𝑥
[𝑐1 cos 𝛽𝑥 + 𝑐2 𝑠𝑖𝑛 𝛽𝑥 ]
Euler’s identity
𝑒 𝑗𝜃
= 𝑐𝑜𝑠𝜃 + 𝑗𝑠𝑖𝑛𝜃
*** is in radian
R-Formulae
𝑎 𝑐𝑜𝑠𝜃 + 𝑏 𝑠𝑖𝑛𝜃 = 𝑅 cos(𝜃 − 𝜑)
𝑎 𝑠𝑖𝑛𝜃 + 𝑏 𝑐𝑜𝑠𝜃 = 𝑅 sin(𝜃 + 𝜑)
𝑅 = 𝑎2 + 𝑏2, 𝜑 = 𝑡𝑎𝑛−1
𝑏
𝑎
𝐹𝑠 = 𝑟𝑒𝑠𝑡𝑜𝑟𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒](https://image.slidesharecdn.com/6-oscillatorymotionfinished-130619233326-phpapp01/85/6-oscillatory-motion-finished-2-320.jpg)
![Graph plotted when 𝝋 = 𝟎𝑑2
𝑥
𝑑𝑡2
= −𝜔2
𝑥
𝑥′′
+ 0𝑥′
+ 𝜔2
𝑥 = 0
Change form,
𝑚2
+ 𝜔2
= 0
𝑚2
= −𝜔2
𝑚 = 𝑗𝜔
𝑚 = ±𝑗𝜔
The roots are complex (𝑚 = 0 ± 𝑗𝜔)
𝑥 𝑡 = 𝑐1 cos 𝜔𝑡 + 𝑐2 𝑠𝑖𝑛 𝜔𝑡
Using R-Formulae,
𝑥 𝑡 = Acos(𝜔𝑡 + 𝜑)
Or
𝒙 𝒕 = 𝐀𝐬𝐢𝐧(𝝎𝒕 + 𝝋)
𝒗 𝒕 =
𝒅𝒙
𝒅𝒕
= 𝝎𝐀𝐜𝐨𝐬(𝝎𝒕 + 𝝋)
𝒂 𝒕 =
𝒅𝒗
𝒅𝒕
= −𝝎 𝟐
𝐀𝐬𝐢𝐧(𝝎𝒕 + 𝝋)
***When 𝜑 ≠ 0, the graph is shifted to
the left or right
𝐴 = 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒 𝑚
𝜔 = 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦
𝑟𝑎𝑑
𝑠
𝜑 = 𝑝ℎ𝑟𝑎𝑠𝑒 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 [𝑟𝑎𝑑]
There are Sinusoidal functions as they
can be shifted to the left or right
𝒙 𝒎𝒂𝒙 = 𝑨
𝒗 𝒎𝒂𝒙 = 𝝎𝐀
𝒂 𝒎𝒂𝒙 = −𝝎 𝟐
𝐀
𝒙(𝒕)
𝒗(𝒕)
𝒂(𝒕)
𝑡
𝑡
𝑡
𝐴
−𝐴
𝜔𝐴
−𝜔𝐴
−𝜔2 𝐴
𝜔2 𝐴
𝐹 = −𝑘 𝑠𝑝𝑟𝑖𝑛𝑔 𝑥 = 𝑚𝑎
𝑎 = −
𝑘
𝑚
𝑥, 𝑎 = −𝜔2
𝑥
***every motion with this form of
equation is Simple Harmonic motion
𝑘 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝑜𝑓 𝑠𝑖𝑚𝑝𝑙𝑒 𝑚𝑎ℎ𝑜𝑛𝑖𝑐 𝑚𝑜𝑡𝑖𝑜𝑛
𝑎 = −
𝑘
𝑚
𝑥
𝑎 = −𝜔2
𝑥
𝜔 =
2𝜋
𝑇
= 2𝜋𝑓 =
𝑘
𝑚](https://image.slidesharecdn.com/6-oscillatorymotionfinished-130619233326-phpapp01/85/6-oscillatory-motion-finished-3-320.jpg)
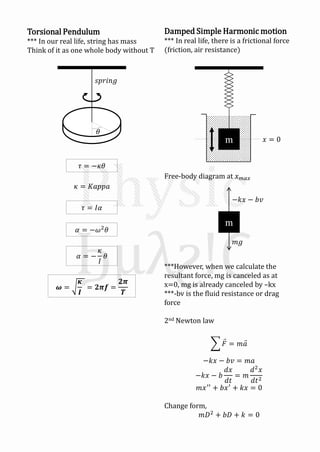
![𝑚𝐷2
+ 𝑏𝐷 + 𝑘 = 0
𝐷 =
−𝑏 ± 𝑏2 − 4𝑚𝑘
2𝑚
𝐷 = −
𝑏
2𝑚
±
𝑏2
4𝑚2
−
𝑘
𝑚
There will be 3 cases
1. If there are 2 distinct roots, 𝐷1, 𝐷2
Over damped
𝑏2
4𝑚2
>
𝑘
𝑚
𝑥(𝑡) = 𝑐1 𝑒 𝑟1 𝑡
+ 𝑐2 𝑒 𝑟2 𝑡
2. If there are a repeated single root, (D)
Critically damped
𝑏2
4𝑚2
=
𝑘
𝑚
𝑥(𝑡) = 𝑐1 𝑒 𝑟𝑡
+ 𝑐2 𝑡𝑒 𝑟𝑡
3. If there are complex roots, (𝛼 ± 𝛽𝑗)
Under damped
𝑏2
4𝑚2
<
𝑘
𝑚
𝑥(𝑡) = 𝑒 𝛼𝑡
[𝑐1 cos 𝛽𝑡 + 𝑐2 𝑠𝑖𝑛 𝛽𝑡 ]
The x-t Graph
𝑡
𝑥
𝐶𝑟𝑖𝑡𝑖𝑐𝑎𝑙𝑙𝑦 𝑑𝑎𝑚𝑝𝑒𝑑
𝑂𝑣𝑒𝑟 𝑑𝑎𝑚𝑝𝑒𝑑
𝑈𝑛𝑑𝑒𝑟 𝑑𝑎𝑚𝑝𝑒𝑑
In this level, we will learn only
underdamped;
𝑏2
4𝑚2 <
𝑘
𝑚
Suppose, 𝛾 =
𝑏
2𝑚
, 𝜔0 =
𝑘
𝑚
𝛾 = 𝑑𝑎𝑚𝑝𝑖𝑛𝑔 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
𝜔0 = 𝑢𝑛𝑑𝑎𝑚𝑝𝑒𝑑 𝑛𝑎𝑡𝑢𝑟𝑎𝑙 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦
Since, 𝐷 = −
𝑏
2𝑚
±
𝑏2
4𝑚2 −
𝑘
𝑚
𝐷 = −𝛾 ± 𝑗 𝛾2 − 𝜔0
2
𝐷 = −𝛾 ± 𝑗 𝜔0
2 − 𝛾2
𝑥(𝑡) = 𝑒−𝛾𝑡[𝑐1 cos 𝑡 𝜔0
2 − 𝛾2 + 𝑐2 𝑠𝑖𝑛 𝑡 𝜔0
2 − 𝛾2 ]
𝑥(𝑡) = 𝑒−𝛾𝑡
[𝐴 sin 𝑡 𝜔0
2 − 𝛾2 + 𝜑 ]
Suppose 𝜔′
= 𝜔0
2 − 𝛾2
𝐴 = 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑎𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒
𝑒−𝛾𝑡
𝑤𝑖𝑙𝑙 𝑚𝑎𝑘𝑒 𝑡ℎ𝑒 𝐴 𝑑𝑖𝑒 𝑑𝑜𝑤𝑛
𝑥(𝑡) = 𝐴𝑒−𝛾𝑡
cos 𝜔′
𝑡 + 𝜑 ]](https://image.slidesharecdn.com/6-oscillatorymotionfinished-130619233326-phpapp01/85/6-oscillatory-motion-finished-7-320.jpg)