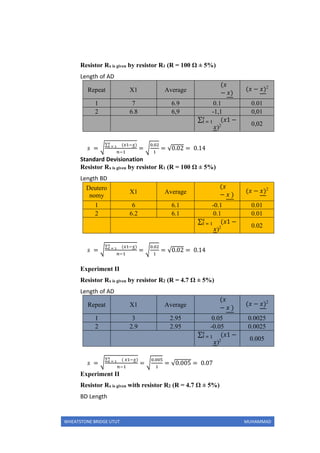
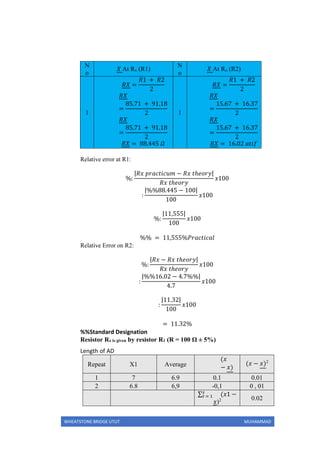
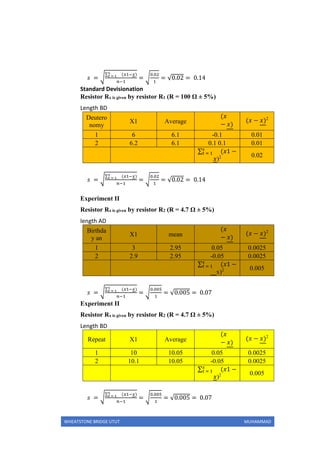
This practicum report describes experiments using a Wheatstone bridge circuit to determine unknown resistor values. The objectives are to determine resistor values indirectly and more accurately compared to using Ohm's law alone. Two experiments are conducted to find unknown resistor values paired with resistors of known values. The first experiment estimates the unknown resistor at 85.71 ohms and the second at 15.67 ohms. Some error is observed in the measurements. The report concludes by discussing sources of error and reviewing the application of Wheatstone bridge principles.

1. PRACTICUM REPORT
BASIC PHYSICS II
"WHEATSTONE BRIDGE"
COLLECTION DATE: 13th
of March 2018 M
DATEPRACTICUM: 14th
of March 2018 M
"WHEATSTONE BRIDGE"
PRACTICUM FINAL PROJECT PRACTICUM
A. OBJECTIVES
1. Can determine the price of obstacles using the Wheatstone bridge
method.
2. Understanding the Wheatstone Bridge method.
3. Comparing the resistance values used when practicing with the
resistance values calculated.
4. Knowing the principle of the Wheatstone Bridge work.
5. Prove how much the unknown resistor value in series and parallel
circuit.
B. BASIC THEORY
The Wheatstone bridge is a method used to measure unknown
obstacles. In addition, the Wheatstone bridge is used to correct errors that
can occur in measuring barriers using Ohm's Law. (Sutrisno. File.upi.edu).
The Wheatstone bridge is a method to measure obstacles indirectly
and more accurately when compared to Ohmmeter. If the Wheatstone
galvanometer bridge circuit shows zero, then the multiplication of obstacles
facing each other is equal. (Cunayah, 2006: 422)
The Wheatstone bridge was discovered by Samuel Hunter Christie
in 1833 and developed by Sir Charles Wheatstone in 1843. The Wheatstone
bridge is an arrangement of electrical circuits to measure an unknown price
barrier. The usefulness of the Wheatstone bridge is to measure the value of
an obstacle by means of a current on the D galvanometer so that cross

2. WHEATSTONE BRIDGE UTUT MUHAMMAD
multiplication can be formulated. The way it works is the electric circuit in
four resistances and the voltage source connected through two diagonal
points on the other two diagonals where the galvanometer is placed.
(Pratama, 2010: 387)
Galvanometer itself is a device that can measure very small currents.
The galvanometer in the process uses a swivel roll current which consists of
an immovable magnet and a piece of wire which is one part that is easily
moved and passed by an electric current. (Suryanto, 1999: 4)
The working principle of Wheatstone barriers is often used in
determining a resistance value or impedance in an electrical circuit. But also
on the resistance given the electron flow wire. The higher the resistance the
smaller the current for one voltage V we then define the resistance so that
the current is inversely proportional to the resistance. When we combine
this with the comparison above. We get 𝐼 =
𝑉
𝑅.
This relationship is often
written 𝑉 = 𝐼 𝑥 𝑅 but is more of a description of a particular class of
material. Resistors have obstacles ranging from less than one Ohm to
millions of Ohms. (Giancoli, 2001: 74)
R1, R2, and R3 have known obstacles, while Rx is an obstacle that
will be sought for magnitude. In the galvanometer, equilibrium state will
show zero. Because there is no current flowing in the galvanometer.
Electrical resistance is a characteristic of an electrical conductor/conductor,
which can be used to regulate the amount of electric current passing through
a circuit. (Sugiyono, 2009: 92)
C. TOOLS AND MATERIALS
NO IMAGES
NAME OF TOOLS AND
MATERIALS
1
Rheostat
(one fruit)

3. WHEATSTONE BRIDGE UTUT MUHAMMAD
2
Galvanometer
(one piece)
3
Power Supply
(one piece)
4
Resistors
(One)
5
Connecting Cable
(sufficient)
6 RULES
D. OF WORK STEPS
NO IMAGES WORK STEP
1 Prepare tools and materials

4. WHEATSTONE BRIDGE UTUT MUHAMMAD
2
Connect the power supply
with Rheostat
3
Connect the rheostat with the
resistor board
4
Connect rheostat with the
galvanometer
Experiment I
Series Series
NO IMAGES WORK STEP
1
When the device is ready to
make a series
2
Resistor boards are made in
series and connected with a
Galvanometer.
3 Turn on the power

5. WHEATSTONE BRIDGE UTUT MUHAMMAD
4
Look at the galvanometer, in
the galvanometer position to
the left.
5
Set the rheostat so that the
galvanometer is zero.
Experiment II
Parallel Circuit
NO IMAGE WORK STEP
1
When the tool is ready to
make a parallel circuit
2
Resistor boards are made in
parallel and connected with a
Galvanometer.
3 Turn on the power
4
Look at the galvanometer, in
the galvanometer position to
the left.

6. WHEATSTONE BRIDGE UTUT MUHAMMAD
5
Set the rheostat so that the
galvanometer is zero.
E. DATA EXPERIMENT
Experiment I
Resistor Rx is given with resistor R1 (R = 100 Ω ± 5%)
Repeat AD Length (cm) Length BD (cm)
1 7 6
2 6.8 6,2
Average 6,9 6, 1
Value 100 ± 5% 100 ± 5%
Experiment II
Resistor Rx is given with resistor R2 (R = 4.7 Ω ± 5%)
Repeat AD Length (cm) Length BD (cm)
1 3 10
2 2.9 10 , 1
Average 2.95 10.05
Value 4.7 ± 5% 4.7 ± 5%
Experiment III
Value of resistor Rx generated data above
No State R values Ω
1 Rx is given with R1 100 Ω ± 5 %
2 Rx is given with R2 4.7 Ω ± 5%
F. DATA PROCESSING
Rx value :
Rx at R1: 𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐷

7. WHEATSTONE BRIDGE UTUT MUHAMMAD
Rx on R2: 𝑅𝑥 =
𝑅2 𝑥 𝐵𝐷
𝐴𝐷
On R1 resistor known: brown, black, chocolate, and gold
In resistor R2 it is known: yellow, purple, gold, and gold
N
o
Rx on R1
N
o
Rx on R2
1
Dik:
R1 = 100 Ω
BD = 6 cm / 6, 10−2
AB = 7 cm / 7, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
100 𝑥 6.10−2
7, 10−2
𝑅 = 85.71 𝛺
1
Dik:
R1 = 4.7 Ω
BD = 10 cm / 10, 10−2
AB = 3 cm / 3, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
4.7 𝑥 10.10−2
3, 10−2
𝑅 = 15.67 𝛺
2
Dik:
R1 = 100 Ω
BD = 6.2 cm / 6.2, 10−2
AB = 6.8 cm / 6.8, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
100 𝑥 6.2.10−2
6.8, 10−2
𝑅 = 91.18 𝛺
2
Dik:
R1 = 4.7 Ω
BD = 10.1 cm / 10.1, 10−2
AB = 2.9 cm / 2.9, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥 =
4.7 𝑥 10.1,10−2
2.9, 10−2
𝑅 = 16.37
rata Average
N
o
𝑋 At Rx (R1)
N
o
𝑋 At Rx (R2)
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋 = 88,445 𝛺
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋 = 16.02 𝛺
Standard Designation

8. WHEATSTONE BRIDGE UTUT MUHAMMAD
Resistor Rx is given by resistor R1 (R = 100 Ω ± 5%)
Length of AD
Repeat X1 Average
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 7 6.9 0.1 0.01
2 6.8 6,9 -1,1 0,01
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0,02
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.02
1
= √0.02 = 0.14
Standard Devisionation
Resistor Rx is given by resistor R1 (R = 100 Ω ± 5%)
Length BD
Deutero
nomy
X1 Average
(𝑥
− 𝑥 )
(𝑥 − 𝑥)2
1 6 6.1 -0.1 0.01
2 6.2 6.1 0.1 0.01
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.02
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.02
1
= √0.02 = 0.14
Experiment II
Resistor Rx is given by resistor R2 (R = 4.7 Ω ± 5%)
Length of AD
Repeat X1 Average
(𝑥
− 𝑥 )
(𝑥 − 𝑥)2
1 3 2.95 0.05 0.0025
2 2.9 2.95 -0.05 0.0025
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.005
𝑠 = √
∑ 𝑠
𝑡 = 1 ( 𝑥1−𝑥)
𝑛−1
= √
0.005
1
= √0.005 = 0.07
Experiment II
Resistor Rx is given with resistor R2 (R = 4.7 Ω ± 5%)
BD Length

9. WHEATSTONE BRIDGE UTUT MUHAMMAD
Deutero
nomy
X1 Average
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 10 10.05 0.05 0.0025
2 10.1 10.05 -0.05 0.0025
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.005
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1− 𝑥)
√ √ 𝑛 − 1 = 0.005 1 = 0.005 =
Relative error on
𝑅1: %:
|𝑙𝑎𝑏 − 𝑅𝑥 𝑅𝑥𝑡ℎ𝑒𝑜𝑟𝑦|
𝑅𝑥𝑡ℎ𝑒𝑜𝑟𝑦
𝑥100%%:
| |
88445 − 100100
𝑥100%%:
|11 555|
𝑥100%
100% = 11,555%
Relative Error on R2:
%:
|𝑅𝑥 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑢𝑚 − 𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦|
𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦
𝑥100
:
|%%16.02 − 4.7%%%%|
4.7
𝑥100
:
|11.32|
100
𝑥100
= 11.32%
G. DISCUSSION
In this practice, the Wheatstone bridge aims to find the resistance
value Rx. In this lab two repetitions were conducted, where each experiment
was repeated twice.
Obstacles to be sought or unknown is carried out by shifting the
rheostat until the galvanometer shows zero. The power supply that is used
to flow electricity so that the needle on the galvanometer can move.

10. WHEATSTONE BRIDGE UTUT MUHAMMAD
In the first experiment using a resistor of 100 ± 5%, a resistor value
that is almost close to that value is obtained. This can be caused by an error
when looking at the value on the rheostat measured by a ruler at the time of
the lab. In this first experiment, the participant assembled the resistor in
series, before looking for an unknown resistor value the practitioner must
know the resistance value in R1. By looking at the color code, or by using
multitester. When the power supply is turned on, the galvanometer needle
will deviate, this means that there is an electric current flowing to the
galvanometer because the working principle of the Wheatstone bridge is a
balance, the galvanometer needle must be at zero by sliding the rheostat. If
it is at zero, this means that there are no more currents flowing in a state as
said to be balanced. This experiment is in accordance with Ohm's Law I,
Kirchof I which states in a closed circuit, the number of algebra GGL (E)
and the number of potential decreases equal to zero.
In the second experiment using a 4.7 Ω ± 5% resistor, the resistance
value is not close to the resistor value. When compared with the resistor
color that has been known the value is quite very far. In this second
experiment, we are assembling a series in a parallel series and an unknown
resistor value, an unknown value resistor when the circuit is larger than the
paralleled circuit.
Between the first experiment and the second experiment is actually
the same, it's just that the resistor used is different in value. This difference
in the value of the resistor can be influenced by happiness factors such as
incorrectly seeing the resistor's color ring and causing an error in its value.
In this experiment, experiments have been conducted on Wheatstone
bridges to find the value of the obstacles that are not yet known. Practically
doing two repetitions, namely the first experiment R which has not known
the obstacle is given with R1 which is 85.71 𝛺and in the second experiment
on R2 is 15, 67 ohms, this data is data in the first experiment with RI and
R2.

11. WHEATSTONE BRIDGE UTUT MUHAMMAD
Of course in this lab there are still mistakes that occur in the
experiment of this Wheatstone bridge which, among others, when looking
at the galvanometer needle, the needle is not exactly zero and when looking
at the needle, the eye with the pointer is not straight, and when measuring
AD length , and the length of BD, not very careful because of the limited
space for rheostats to measure the length of the AD and the length of BD,
and the practitioner can carry out this experiment until it is finished with the
guidance of Ika.
H. POST PRACTICUM TASKS
1. Calculate the resistor resistance generated in steps 1, and 2!
Answer:
N
o
Rx on R1
N
o
Rx on R2
1
Dik:
R1 = 100 Ω
BD = 6 cm / 6, 10−2
AB = 7 cm / 7, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
100 𝑥 6.10−2
7, 10−2
𝑅 = 85.71 𝛺
1
Dik:
R1 = 4.7 Ω
BD = 10 cm / 10, 10−2
AB = 3 cm / 3, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
4.7 𝑥 10.10−2
3, 10−2
𝑅 = 15.67 𝛺
2
Dik:
R1 = 100 Ω
BD = 6.2 cm / 6.2, 10−2
AB = 6.8 cm / 6.8, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥
=
100 𝑥 6.2.10−2
6.8, 10−2
𝑅 = 91.18 𝛺
2
Dik:
R1 = 4.7 Ω
BD = 10.1 cm / 10.1, 10−2
AB = 2.9 cm / 2.9, 10−2
Dit Rx?
𝑅𝑥 =
𝑅1 𝑥 𝐵𝐷
𝐴𝐵
𝑅𝑥 =
4.7 𝑥 10.1,10−2
2.9, 10−2
𝑅 = 16.37
rata Average

12. WHEATSTONE BRIDGE UTUT MUHAMMAD
N
o
𝑋 At Rx (R1)
N
o
𝑋 At Rx (R2)
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋 = 88,445 𝛺
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋 = 16.02 𝑎𝑡𝑖𝑓
Relative error at R1:
%:
|𝑅𝑥 𝑝𝑟𝑎𝑐𝑡𝑖𝑐𝑢𝑚 − 𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦|
𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦
𝑥100
:
|%%88.445 − 100|
100
𝑥100
%:
|11,555|
100
𝑥100
%% = 11,555%𝑃𝑟𝑎𝑐𝑡𝑖𝑐𝑎𝑙
Relative Error on R2:
%:
|𝑅𝑥 − 𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦|
𝑅𝑥 𝑡ℎ𝑒𝑜𝑟𝑦
𝑥100
:
|%%16.02 − 4.7%%|
4.7
𝑥100
:
|11.32|
100
𝑥100
= 11.32%
%%Standard Designation
Resistor Rx is given by resistor R1 (R = 100 Ω ± 5%)
Length of AD
Repeat X1 Average
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 7 6.9 0.1 0.01
2 6.8 6,9 -0,1 0 , 01
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.02

13. WHEATSTONE BRIDGE UTUT MUHAMMAD
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.02
1
= √0.02 = 0.14
Standard Devisionation
Resistor Rx is given by resistor R1 (R = 100 Ω ± 5%)
Length BD
Deutero
nomy
X1 Average
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 6 6.1 -0.1 0.01
2 6.2 6.1 0.1 0.1 0.01
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.02
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.02
1
= √0.02 = 0.14
Experiment II
Resistor Rx is given by resistor R2 (R = 4.7 Ω ± 5%)
length AD
Birthda
y an
X1 mean
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 3 2.95 0.05 0.0025
2 2.9 2.95 -0.05 0.0025
∑ 𝑠
𝑡 = 1 (𝑥1 −
x)2 0.005
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.005
1
= √0.005 = 0.07
Experiment II
Resistor Rx is given by resistor R2 (R = 4.7 Ω ± 5%)
Length BD
Repeat X1 Average
(𝑥
− 𝑥)
(𝑥 − 𝑥)2
1 10 10.05 0.05 0.0025
2 10.1 10.05 -0.05 0.0025
∑ 𝑠
𝑡 = 1 (𝑥1 −
𝑥)2 0.005
𝑠 = √
∑ 𝑠
𝑡 = 1 (𝑥1−𝑥)
𝑛−1
= √
0.005
1
= √0.005 = 0.07

14. WHEATSTONE BRIDGE UTUT MUHAMMAD
2. Compare the resistor resistance produced!
Answer:
N
o
𝑋 at Rx (R1)
N
o
𝑋 At Rx (R2)
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋
=
85.71 + 91.18
2
𝑅𝑋 = 88,445 𝛺
1
𝑅𝑋 =
𝑅1 + 𝑅2
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋
=
15.67 + 16.37
2
𝑅𝑋 = 16.02 𝑎𝑡𝑖𝑓
Relative Error in R1: (% = 11.555%)
Relative Error on R2: ( % = 11.320%)
In this resistance, the resistor value is different from the value of
resistor R1 and R2, why? Because maybe when practicum the practitioner
is not careful when looking at the data on the rheostat, and also different
from the resistor value so that the value of resistor R1 is R = 100 Ω ± 5%,
and at R2 is R = 4.7 7 ± 5 %. The bigger result is in the series in R1, meaning
that the resistor color ring is very influential to determine the value of this
Wheatstone bridge practicum.
I. CONCLUSION
Based on the practicum that has been done, it can be concluded that:
1. The Wheatstone bridge uses Kirchoff Law one and two where the
currents at both ends are equal to produce a value of 0 on the
galvanometer.
2. The Wheatstone bridge method is used to measure the obstacle
method which is not yet known by multiplying it by crossing.
3. The Wheatstone bridge can be used to find the value of an unknown
value.

15. WHEATSTONE BRIDGE UTUT MUHAMMAD
4. The working principle of the Wheatstone bridge uses three laws,
namely: Ohm's Law, I Kirchoff's Law, Kirchoff's II Law.
5. The Rx value is greater when it is set to R1, because of the larger
resistor value.
J. COMMENTS
a. It is recommended that the practitioners prior to doing the practicum
have to learn what they will practice in order to make the circuit
correctly.
b. It is expected that when doing a practicum, the practitioner must be
more careful.
c. Practically there must be mutual cooperation in this Wheatstone
bridge practicum.
K. REFERENCES
Cunayah. (2006). Physics. Jakarta: Erlangga
Giancoli, DC (2001). Basic Physics Volume 2. Jakarta: Erlangga.
Primary. (2010). physics of electrical materials. Yogyakarta: learning library.
Sugiyono, Vani. (2009). Physics. Surabaya: PT. Friend Library.
Suryanto. (1999). Physics measurement technique. Jakarta: Erlangga.
Sutrisno. upi file. Wheatstone bridge.pdf. Jakarta: Erlangga
L. APPENDIX