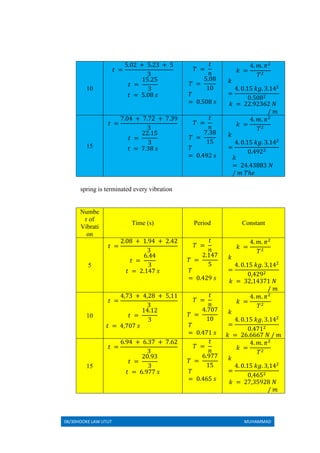
Utut Muhammad conducted experiments to determine spring constants in single, series, and parallel circuits. In the single circuit experiment, the spring constant was determined to be 11 N/m. In the parallel circuit experiment, the total spring constant increased compared to individual springs. In the series circuit experiment, the total spring constant decreased compared to individual springs due to the total length increase being the sum of the individual spring lengths.

1. FINAL REPORT PRACTICUM
BASIC PHYSICS II
"Hooke's Law"
NAME: Utut Muhammad
"HOOKE’S LAW"
PRACTICUM FINAL PROJECT PRACTICUM
A. OBJECTIVE
1. Determine spring constants in a single circuit , serial, and parallel.
2. Analyze the relationship between force and increase in spring length.
3. Analyzing the relationship between added spring length and spring
constant affects the string value.
4. Determine the spring period in single, series, and parallel circuits.
B. BASIC THEORY
Each object will change when the style is done on it. If the forces
are large enough, the object in question can be broken, or fractured
(fracture). The segment on the curve that starts from the starting point to
the elastic boundary point is called the elastic region. If an object is
stretched over the elastic boundary, the object will enter the plastic region:
the object will no longer return to its original length if the external force is
removed from the object but will deform permanently. The maximum
length change will be achieved at the breaking point. (Giancoli, 2014: 302-
303)
Hooke's Law is a provision regarding the force that occurs because
of its elastic nature and spring the magnitude of the hook force will usually
be directly proportional to the distance of the spring and its normal
position. The force carried out by spring if it is pressed or stretched is the
result of the intermolecular force of a complicated force in spring, but the
empirical picture of the macroscopic agent of the spring is sufficient for

2. 08/30HOOKE LAW UTUT MUHAMMAD
most applications. If the spring is pressed or stretched then it is released
back to its origin or natural length, if the displacement is not too large.
There is a limit to that move. Above that value, the spring does not return
to its original length but remains permanently in a changed state. If we only
allow displacement below this limit, we can calibrate the stretch or
𝑝𝑟𝑒𝑠𝑠 ∆𝑥 through the force needed to produce the stretch. Experimentally
it was found that for ∆𝑥 small, the force carried out by the spring
approaches proportional to ∆𝑥 and in the opposite direction. This
relationship is known as Hooke's Law, which can be written: 𝐹𝑥 =
−𝑘 (𝑋1 − 𝑋0) = −𝑘∆𝑥. (Tipler, 1998: 102)
Hooke's law is the relationship between springs and other elastic,
provided that the results are not too large if an object can be deformed
through a certain point, it will not return to its original form if the force
imposed on it is removed, the point is called elastic point. For materials in
general, Hooke's Law applies to regions below their elastic boundary
points. Areas of style that fulfill Hooke's Law are referred to as
"proportional areas". Beyond elastic limits. Style is no longer expressed by
the power potential function, if the deformed solid material we release, it
will fight like a simple harmonic oscillator. So, during the amplitude the
vibration is quite small, or as long as the deformation remains in the
proportional area. (Haliday, 1978: 445).
Still remember for the ideal spring statement that is pressed or
stretched as far as X, in this section the spring is ideally defined as a spring
which when pressed or stretched gives the force 𝐹 = −𝑘∆𝑥, referred to
as the force constant, a joint object m attached to a spring ideal with the R
force constant and free to move above the frictionless surface is one
example of a simple harmonic insulator. If the object deviates to it, the
force carried out by the spring is directed to the left and given by 𝐹 =
−𝑘∆𝑥, this force is the OHS recovery force. (Halliday, 1978: 447)

3. 08/30HOOKE LAW UTUT MUHAMMAD
A spring phenomenon that is subjected to external forces then the
force is removed, and the spring will return to its original state, observed
by Robert Hooke. Robert Hooke (1635-1703) is an English scientist. Hooke
put forward his law known as Hooke's law with sound as follows:
"In the area of object elasticity, the magnitude of the change in
length is proportional to the force acting on objects."
Basically, Hokum Hooke illustrates that if a spring is given force (F),
then the force will be proportional straight with a change in Length (Δx) on
the spring. 𝐹= -𝑘∙ Δ𝑥, The minus sign indicates that the spring will tend to
resist change. In the sense that the direction is opposite to the deviation.
(Ishaq, Mohammad.2007: 142)
A statement about Hooke's Law was put forward by Robert Hooke.
Robert Hooke is an architect. (Kanginan, 2013: 235) The
increase in spring length depends on the amount of gravity
dependent, also because of the spring behavior, for the same load force, a
more rigid increase in spring length will be smaller than the increase in
spring length with a smaller stiffness. The stiffness of a spring is indicated
by a value. The stiffness of a spring is indicated by a value. Characteristics
called spring force constants or abbreviated spring constants (k), the
greater the value of k, the stiffer the spring becomes. (Raharja, 2013: 128)
In series, the force acting on each spring is the same and the
increase in length is the total of all the spring joints. The series
arrangement aims to reduce the spring constant so that the length
increments experienced by the spring system will be more. Mathematically
decreases the formula for spring replacement constants in series, namely:

4. 08/30HOOKE LAW UTUT MUHAMMAD
(https: //www.google.co.id/ 2014 / 08/30 / search? Q = image + spring
+ series + and + parallel /)
𝑊 = 𝐹1 = 𝐹2 = 𝐹
∆𝐿 = ∆𝐿1 + ∆𝐿2
𝐹
𝐾𝑃
=
𝐹1
𝑘1
+
𝐹2
𝑘2
𝑊
𝐾𝑝
=
𝑊
𝑘1
+
𝑊
𝐾2
𝑊
𝐾𝑝
= 𝑊 (
1
𝑘1
+
1
𝑘2
)
1
𝐾𝑝
=
1
𝑘1
+
1
𝑘2
In parallel circuits, springs are connected in parallel with the
distance between springs is the same, but the resultant force acting on the
spring is the total of each force acting on each spring. Therefore, each
spring experiences an equal increase in length, which is equal to the
increase in the length of the spring system. The parallel arrangement aims
to increase the spring constant so that the increase in the length of the
spring system is smaller than that of the series arrangement.
Mathematically decreases the formula for spring replacement constants in
parallel circuits, namely:

5. 08/30HOOKE LAW UTUT MUHAMMAD
(https: //www.google.co.id/145/30/search? Q = image + spring +
series + and + parallel /)
∆𝐿 = 𝐿1 = 2𝐿2 = ∆𝐿3
𝐹 = 𝐹1 + 𝐹2 + 𝐹3
𝐾𝑝, ∆𝐿 = 𝑘1, 𝐿 + 𝑘2, 𝐿 + 𝑘3, 𝐿
𝐾𝑝, ∆𝐿 = ∆𝐿 (𝑘1 + 𝑘2 + 𝑘3)
𝐾𝑝 = 𝑘1 + 𝑘2 + 𝑘3
Where: kp is the substitute constant (N / m), ∆𝐿 is the increase in
length (m), F is the force (N), and W is the weight (N).
Note:
● In series, if at the end of the spring arrangement the force (F),
then each spring gets the same force that is F.
● In the parallel circuit, the total spring constant for the parallel
spring circuit according to Hooke's Law is as long as the force (F)
increases the length of each spring is large.
(Mikrajuddin, 2016: 499-500)
C. TOOLS AND MATERIALS

6. 08/30HOOKE LAW UTUT MUHAMMAD
N
O
PICTURES
NAME OF
TOOLS AND
MATERIALS
AMOUNT
1 Statif
1 Fruit
2 Spring
2 Fruit
3 200 gram load
1 Set
4 Timer
1 Fruit
5 isolatif
Moderation
6 Chopsticks
1 Fruit

7. 08/30HOOKE LAW UTUT MUHAMMAD
7 Ruler
1 Fruit
8 Statif Clamp
1 Fruit
D. WORK STEP
Experiment I
On Spring and Load
NO IMAGE WORK STEP
1 Install the Statif
2
Hang the spring at the stand
and measure the spring length
of the spring.
3
Measure the length of a spring
that is added to load

8. 08/30HOOKE LAW UTUT MUHAMMAD
4 Give a deviation of 9 cm
5
Remove the load
simultaneously with the
stopwatch
6
Calculate the time needed by
the spring at 5s, 10s and 15s.
7
Repeat steps in number 6 for 3
attempts
Experiment II
Parallel Circuits
NO IMAGES WORK STEP
1
Assemble it in parallel with the
statif, hang the chopsticks in
the middle of the two springs
and measure the initial length
of the spring.

9. 08/30HOOKE LAW UTUT MUHAMMAD
2
Insulate the spring so that
when the spring is used it
doesn't go anywhere.
3 Give a deviation of 9 cm
4
Release the load together with
the stopwatch.
5
Calculate the time needed by
the spring at 5s, 10s, and 15s.
6
Repeat steps in number 5 for 3
trials
Experiment III
Series Series
NO IMAGES WORK STEP

10. 08/30HOOKE LAW UTUT MUHAMMAD
1
Arrange it in series with the
string, hang the chopsticks in
the middle of the two springs
and measure the initial length
of the spring.
2
Insulate the spring so that
when the spring is used it
doesn't go anywhere.
3 Give a deviation of 9 cm
4
Release the load together with
the stopwatch.
5
Calculate the time needed by
the spring at 5s, 10s, and 15s.
6
Repeat steps in number 5 for 3
trials.
E. DATA EXPERIMENT

11. 08/30HOOKE LAW UTUT MUHAMMAD
Experiment I
On Spring andLoad
Mass : 15 x 10-2
kg
Initial length : 17 x 10-2
m
Final length : 25 x 10-2
m
Added length : 8 x 10-2
m
No.
Amount of
Vibration
Time (s)
Not
dismissedstopped
Every vibration is
1
5 03.46 04.53
10 07.42 08.61
15 11.58 12.55
2
5 03.35 03.51
10 07.31 06.97
15 10 ,
50 10.35 3 5 03.81
03.24 10 07.61
Experiment II
Series of Parallel
Mass: 15 x 10-2
kg
initial length:17 x 10-2
m
length end : 20 x10-2
m
Length increase : 3 x 10-2
m
No.
Amount of
Vibration
Time (s)
No dismissal
Discharged every
vibration
1 5 03.03 02.08

12. 08/30HOOKE LAW UTUT MUHAMMAD
10 05.02 04.73
15 07.04 06.94
2
5 04.42 01.94
10 05.23 04.28
15 07 , 72 06,37
3
5 02,39 02,42
10 05,00 05,11
15 07,39 07,62
Experiment III
Series
Mass : 15 x 10-2
kg
Initial length : 37 x 10-2
m
Final length : 61 x 10-2
m
Increase in length : 24 x 10-2
m
No.
Amount of
Vibration
Time (s)
No dismissal
Termination of
each vibration
1
5 06.30 06.15
10 12.59 12.12
15 19.49 18.09
2
5 05.93 06.40
10 12.31 12.18
15 18 , 58 18.10
3
5 06.40 05.20
10 12.60 10.81
15 19.16 16.60
F. PROCESSING OF DATA

13. 08/30HOOKE LAW UTUT MUHAMMAD
Experiments I
Single
Mass : 15 x 10-2
kg
Initial length : 17 x 10-2
m
Final length : 25 x 10-2
m
Length increase : 8 x 10-2
m
Spring is not stopped
Numbe
r of
Vibrati
on
Time Period Constant
5
𝑡
=
03,46 + 03,35 + 03,81
3
𝑡 =
10.62
3
𝑡 = 3.54 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
3.54 𝑠
5
𝑇
= 0.708 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7082
𝑘 = 11.80169 𝑁
/ 𝑚
10
𝑡 =
7.42 + 7.31 + 7.61
3
𝑡 =
22.34
3
𝑡 = 7.45 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
7.45 𝑠
10
𝑇
= 0.745 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7452
𝑘 = 10.65855 𝑁
/ 𝑚
15
𝑡
=
11.58 + 10.5 + 11.25
3
𝑡 =
33.33
3
𝑡 = 11.11𝑠
𝑇 =
𝑡
𝑛
𝑇 =
11.11 𝑠
15
𝑇
= 0.741 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7412
𝑘
= 10.77393 𝑁
/ 𝑚 𝑇ℎ𝑒
spring is stopped every vibration
Numbe
r of
Vibrati
on
Time (s) Period Constant

14. 08/30HOOKE LAW UTUT MUHAMMAD
5
𝑡 =
4.53 + 3.51 + 3.24
3
𝑡 =
11.28
3
𝑡 = 3 , 76 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
3.76 𝑠
5
𝑇
= 0.752 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7522
𝑘 = 10.46104 𝑁
/ 𝑚
10
𝑡 =
8.61 + 6.97 + 6.96
3
𝑡 =
22.54
3
𝑡 = 7.51 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
7.51 𝑠
10
𝑇
= 0.751 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7512
𝑘 = 10.48892 𝑁
/ 𝑚
15
𝑡
=
12.55 + 10.35 + 10.66
3
𝑡 =
33.56
3
𝑡 = 11.19𝑠
𝑇 =
𝑡
𝑛
𝑇 =
11.19 𝑠
15
𝑇
= 0.746 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.7462
𝑘 = 10.62999 𝑁
/ 𝑚
Experiment II
Parallel
Mass : 15 x 10-2
kg
Initial length : 17 x 10-2
m
Final length : 20, x 10-2
m
Added length : 3 x 10-2
m
Spring not terminated
Numbe
r of
Vibrati
on
Time (s) Period Constant
5
𝑡 =
3.03 + 4.42 + 2.39
3
𝑡 =
9.84
3
𝑡 = 3.28 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
3, 28
5
𝑇
= 0.656 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.6562
𝑘 = 13.74684 𝑁
/ 𝑚

15. 08/30HOOKE LAW UTUT MUHAMMAD
10
𝑡 =
5.02 + 5.23 + 5
3
𝑡 =
15.25
3
𝑡 = 5.08 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
5.08
10
𝑇
= 0.508 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.5082
𝑘 = 22.92362 𝑁
/ 𝑚
15
𝑡 =
7.04 + 7.72 + 7.39
3
𝑡 =
22.15
3
𝑡 = 7.38 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
7.38
15
𝑇
= 0.492 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.4922
𝑘
= 24.43883 𝑁
/ 𝑚 𝑇ℎ𝑒
spring is terminated every vibration
Numbe
r of
Vibrati
on
Time (s) Period Constant
5
𝑡 =
2.08 + 1.94 + 2.42
3
𝑡 =
6.44
3
𝑡 = 2.147 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
2.147
5
𝑇
= 0.429 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3,142
0,4292
𝑘 = 32,14371 𝑁
/ 𝑚
10
𝑡 =
4,73 + 4,28 + 5,11
3
𝑡 =
14.12
3
𝑡 = 4,707 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
4.707
10
𝑇
= 0.471 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
0.4712
𝑘 = 26.6667 𝑁 / 𝑚
15
𝑡 =
6.94 + 6.37 + 7.62
3
𝑡 =
20.93
3
𝑡 = 6.977 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
6.977
15
𝑇
= 0.465 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3,142
0,4652
𝑘 = 27,35928 𝑁
/ 𝑚

16. 08/30HOOKE LAW UTUT MUHAMMAD
Experiment III
in Series
Mass : 15 x 10-2
kg
Initial length : 37 x 10-2
m
Final length : 61 x 10-2
m
Length increase : 24 x 10-2
m The
spring is not stopped
Numbe
r of
Vibrati
on
Time (s) Period Constant
5
𝑡 =
6.3 + 5.93 + 6.4
3
𝑡 =
18.63
3
𝑡 = 6.21 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
6.21 𝑠
5
𝑇
= 1.242 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
1.2422
𝑘 = 3.835018 𝑁
/ 𝑚
10
𝑡
=
12.59 + 12.31 + 12.6
3
𝑡 =
37.5
3
𝑡 = 12.5 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
12.5 𝑠
10
𝑇
= 1.25 𝑠𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
1.252
𝑘 = 3.786086 𝑁
/ 𝑚
15
𝑡
=
19.49 + 18.58 + 19.16
3
𝑡 =
57.23
3
𝑡 = 19.07 𝑠
𝑇 =
𝑡
𝑛
𝑇
=
19 , 07 𝑠
15
𝑇
= 1,272 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3,142
1,2722
𝑘
= 3,656254 𝑁
/ 𝑚 𝑇ℎ𝑒
spring is stopped every vibration
Numbe
r of
Vibrati
on
Time (s) Period Constants

17. 08/30HOOKE LAW UTUT MUHAMMAD
5
𝑡 =
6,15 + 6,4 + 5,2
3
𝑡 =
17.75
3
𝑡 = 5,917 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
5,917 𝑠
5
𝑇
= 1,183 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
1,1832
𝑘 = 4.227086 𝑁
/ 𝑚
10
𝑡
=
12.12 + 12.18 + 10.81
3
𝑡 =
35.11
3
𝑡 = 11.70 𝑠
𝑇 =
𝑡
𝑛
𝑇 =
11.70 𝑠
10
𝑇 = 1.17 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
1.172
𝑘 = 4.321543 𝑁
/ 𝑚
15
𝑡 =
18.09 + 18.1 + 16.6
3
𝑡 =
52.79
3
𝑡 = 17.597 𝑠
𝑇 =
𝑡
𝑛
𝑇
=
17.597 𝑠
15
𝑇
= 1,173 𝑠
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘
=
4. 0.15 𝑘𝑔. 3.142
1,1732
𝑘 = 4,299466 𝑁
/ 𝑚
G. DISCUSSION
In this practicum, the practitioner did several experiments to prove
Hooke's Law, which in the first experiment, used a single spring given a
load of 0.15 kg, in the second experiment using springs arranged in parallel,
and the third experiment uses two springs arranged in series.
In this first experiment, three repetitions were carried out with a
range of 5s, 10s, and 15s. The results of the average time value of each of
the three experiments were obtained. When the spring is not stopped, the
longer the spring takes to do more vibrations. After that, then look for the
value of the period, where the period value is small if the vibrations
experienced are many, the spring period when the single circuit will affect
the spring constant value when the spring is stopped each vibration the value
𝑡 is smaller than when the spring is not stopped .
In the experiment above, it can be seen that the elastic constants of
each spring are different, the value of spring constants arranged singly, the

18. 08/30HOOKE LAW UTUT MUHAMMAD
constant value is greater than compared to the spring constant values
arranged in series because the length increment in a single spring is not too
large compared to the two springs arranged in a series of single spring
constant values are inversely proportional to the length increase and are
directly proportional to the tensile force given. The greater the length
increment in the spring, the smaller the value of the spring constant and the
constant value that is terminated in style are not the same constant.
This experiment, the experimenters conducted by using two springs
arranged in parallel, the two ends are combined using chopsticks, the
direction is to make it easier to load, and given isolation so that the load
does not move right or left. It can be seen in the data above that the two
springs arranged in parallel with the constant values of the two springs are
larger than the single springs and springs arranged in series. This is because
the two springs are arranged in parallel when given a load, the load is
divided between the first spring and the second spring so that the increase
in length is not too large, then the constant value of the spring is large.
Because the constant value is inversely proportional to the length increment.
As for the next experiment, the participants conducted an
experiment using two springs arranged in series. The value of spring
constants arranged in series is smaller than the constant value of the spring
which is arranged in parallel and single spring because the spring arranged
in series has a very large increase in length because the increase in length is
very large, the constant value is small.
In the next experiment, the practitioner obtained data that was not
much different and almost similar to the previous experiment, namely on
the spring, the series spring had a long time to vibrate on many of the same
vibrations compared to the parallel and single springs. value, time, period,
and spring constant.
This time the practicum uses a load of 0.15 kg. The spring treatment
is dismissed or not dismissed also affects the value. So that the external
force acting on this spring also determines the size of the period values and

19. 08/30HOOKE LAW UTUT MUHAMMAD
constants even though they are not so significant. This experiment has been
carried out there are still mistakes that occur, one of which is not right when
using a stopwatch, and sometimes when it's been 5 vibrations, 10 vibrations,
15, the stopwatch's vibration is not vibrated so that there is a difference of a
few seconds. Finally, the practitioner can carry out Hooke's Law practicum
by walking in line as the practicum takes place with the guidance of Diya.
H. POST PRACTICUM TASKS
1. Determine the vibration period based on the results of the practicum data
obtained?
Answer: The
spring is arranged in a single
spring and is not stopped. The spring is stopped
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
11.8
𝑇 = 6.28 𝑥 0.1127
𝑇 = 0.7077 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
10.46
𝑇 = 6.28 𝑥 0.1197
𝑇 = 0.7517 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
10.66
𝑇 = 6.28 𝑥 0.1186
𝑇 = 0.7448 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
10.49
𝑇 = 6.28 𝑥 0.1196
𝑇 = 0.751 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
10.77
𝑇 = 6.28 𝑥 0.118
𝑇 = 0.741 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
10.63
𝑇 = 6.28 𝑥 0.1188
𝑇 = 0.746 𝑠

20. 08/30HOOKE LAW UTUT MUHAMMAD
Spring is arranged in parallel The
spring is not stopped The spring is stopped
𝑇 = 2 = √
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
13.75
𝑇 = 6.28 𝑥 0.1044
𝑇 = 0.656 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
32.14
𝑇 = 6.28 𝑥 0.068
𝑇 = 0.427 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
22.92
𝑇 = 6.28 𝑥 0.081
𝑇 = 0.509 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
26.67
𝑇 = 6.28 𝑥 0.0748
𝑇 = 0.47 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
24.44
𝑇 = 6.28 𝑥 0.078
𝑇 = 0.49 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
27.36
𝑇 = 6.28 𝑥 0.074
𝑇 = 0.464 𝑠
Spring strung in series The
spring is not dismissed The spring is stopped
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
3.83
𝑇 = 6.28 𝑥 0.1977
𝑇 = 1.2416 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
4.23
𝑇 = 6.28 𝑥 0.1883
𝑇 = 1.1825 𝑠

21. 08/30HOOKE LAW UTUT MUHAMMAD
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
3.79
𝑇 = 6.28 𝑥 0.19891.249
𝑇 = 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
4.32
𝑇 = 6.28 𝑥 0.1863
𝑇 = 1.17 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
3.66
𝑇 = 6.28 𝑥 0.2022
𝑇 = 1.27 𝑠
𝑇 = 2𝜋√
𝑚
𝑘
𝑇 = 2. 3.14√
0.15
4.3
𝑇 = 6.28 𝑥 0.1868
𝑇 = 1,173 𝑠
2. Determine the spring constant in the experiment from the practicum
results data?
Answer: The
spring is arranged in a single
spring and the spring is not dismissed,
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7082
𝑘 = 11.80169 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7522
𝑘 = 10.46104 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7452
𝑘 = 10.65855 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7512
𝑘 = 10.48892 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7412
𝑘 = 10.77393 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.7462
𝑘 = 10.62999 𝑁 / 𝑚
Springs are arranged in parallel The

22. 08/30HOOKE LAW UTUT MUHAMMAD
springs are not dismissed The springs are dismissed
=
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.6562
𝑘 = 13.74684 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.4292
𝑘 = 32.14371 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.5082
𝑘 = 22.92362 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3,142
0,4712
𝑘 = 26,66667 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
0.4922
𝑘 = 24.43883 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3,142
0,4652
𝑘 = 27,35928 𝑁 / 𝑚 𝑇ℎ𝑒
spring arranged in series The
spring is not dismissed The spring is dismissed
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1.2422
𝑘 = 3.835018 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1,1832
𝑘 = 4.227086 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1.252
𝑘 = 3.786086 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1.172
𝑘 = 4.321543 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1,2722
𝑘 = 3,656254 𝑁 / 𝑚
𝑘 =
4. 𝑚. 𝜋2
𝑇2
𝑘 =
4. 0.15 𝑘𝑔. 3.142
1,1732
𝑘 = 4,299466 𝑁 / 𝑚
3. Does the initial deviation or the size of the external force affect the size
of the period?
Answer: The

23. 08/30HOOKE LAW UTUT MUHAMMAD
initial deviation and the size of the force do not affect the period,
because the period that is the time needed for the object to do vibration
can be formulated 𝑇 =
𝑡
𝑛
or 𝑇 = 2𝜋√
𝑚
𝑘
. We can draw the conclusion
that from the above formula does not affect the size of the period, which
affects the period is the mass of objects and spring constants.
4. Does mass load affect the spring vibration period? Explain!
Answer:
The mass load effect on the period since the mass of the load is
proportional to period, can be formulated 𝑇 = 2𝜋√
𝑚
𝑘
the greater the
mass, the smaller loads also the spring period. If the load used is large,
the spring will do a lot of vibration and the time it takes to reach
equilibrium.
I. CONCLUSION
Based on the practicum that has been done, it can be concluded that:
1. Each spring circuit affects the value of its constant until its value varies.
The highest constant value, namely in parallel sequences.
2. The greater the force that is given, the more the length of the spring
increases.
3. The largest spring period is in parallel circuits.
4. The value of the spring constant is inversely proportional to the square
of the value of the period.
J. COMMENT
a. It takes quite a long time to do Hooke's Law practicum.
b. Be more careful when doing this lab.
c. Practicing fragrant understand how to arrange series and parallel to
Hooke's Law practicum.
K. REFERENCES
Abdullah, Mikrajuddin. 2016. Basic Physics II. Bandung: Bandung Institute
of Technology
.

24. 08/30HOOKE LAW UTUT MUHAMMAD
Giancoli, Douglas C. 2014. Physics: Principles and Applications of the
Seventh Edition
Volume 1. Jakarta: Erlangga.
Halliday. (1978). Basic Physics I Fifth Edition. Jakarta: Erlangga.
Ishaq, Mohammad.2007.Basic Physics Edition 2.Graduation of Science.
Yogyakarta.
Tipler, Paul. 1998. Physics for Science and Binding Techniques 1. Jakarta:
Erlangga
(https: //www.google.co.id/ 2014 // search? Q = image + spring + series +
and parallel /)
L. APPENDIX