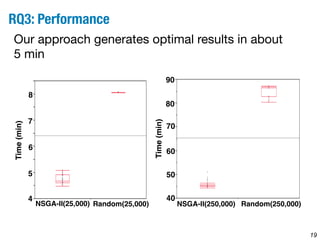
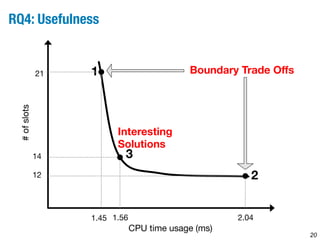
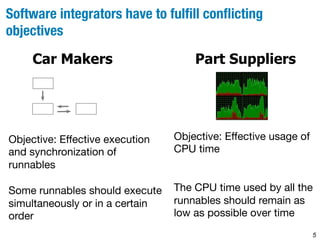
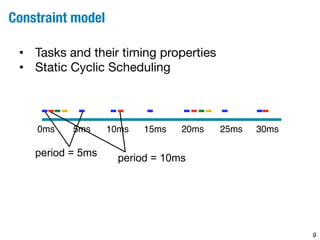
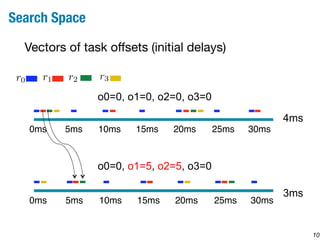
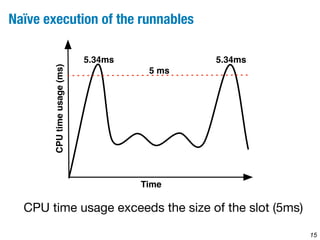
This document describes a method for identifying optimal trade-offs between CPU time usage and temporal constraints in software integration using multi-objective search. The method models the problem as a constrained optimization problem to minimize CPU time usage and number of time slots while satisfying timing constraints. A multi-objective genetic algorithm searches over task offset vectors to find Pareto optimal solutions representing different trade-offs. The approach is evaluated on a large automotive case study with 430 tasks, finding solutions that reduce CPU usage by 60-70% compared to a naive approach.

1. Identifying Optimal Trade-Offs between CPU
Time Usage and Temporal Constraints
Using Search"
Shiva Nejati, Lionel C. Briand"
SnT Centre, University of Luxembourg"
"
"

2. Today’s cars are developed in a distributed way
2

3. Integration of software from different sources is
essential in most embedded software industries
3

4. Software integration involves multiple stakeholders
4
Car Makers
Software
Part Suppliers
Software
Integrator

5. Software integrators have to fulfill conflicting
objectives
5
Car Makers Part Suppliers
Objective: Effective execution
and synchronization of
runnables
Some runnables should execute
simultaneously or in a certain
order
Objective: Effective usage of
CPU time
The CPU time used by all the
runnables should remain as
low as possible over time

6. It is challenging to satisfy all objectives
Car Makers r0 r1 r2 r3 Part Suppliers
Minimize CPU time usage
Execute r0 to r3 close to one another.
0ms 5ms 10ms 15ms 20ms 25ms 30ms
0ms 5ms 10ms 15ms 20ms 25ms 30ms
0ms 5ms 10ms 15ms 20ms 25ms 30ms
6
4ms
3ms
2ms
1 slot
2 slots
3 slots

7. 7
An multi-objective decision support approach
# of slots
2ms 3ms 4ms
CPU time usage
3
2
1
Pareto Front Solutions/
Tradeoff Solutions
Car Makers
Part Suppliers

8. Constrained Optimization Problem (COP)
8
Objective Function(s):
Minimizing CPU time usage
Minimizing # of time slots
Constraint model:
Tasks and their timing properties
Scheduling policy
Search Space:
Vectors of Task Offsets

9. • Tasks and their timing properties
• Static Cyclic Scheduling
0ms 5ms 10ms 15ms 20ms 25ms 30ms
9
Constraint model
period = 5ms period = 10ms

10. 10
4ms
3ms
Search Space
Vectors of task offsets (initial delays)
r0 r1 r2 r3
o0=0, o1=0, o2=0, o3=0
0ms 5ms 10ms 15ms 20ms 25ms 30ms
o0=0, o1=5, o2=5, o3=0
0ms 5ms 10ms 15ms 20ms 25ms 30ms

11. (1) CPU time usage
0ms 5ms 10ms 15ms 20ms 25ms 30ms
11
Objective Functions
(2) Number of Time slots
0ms 5ms 10ms 15ms 20ms 25ms 30ms
Runnables r0, r1, r2, and r3 run in within at most two
consecutive time slots infinitely often iff
for every ri, rj 2 {r0, r1, r2, r3}, for some l < 2
oi ⌘ oj + l ⇥ 5 mod(gcd(periodi, periodj))
3ms

12. 12
Solution Overview

13. 13
Multi-Objective Search algorithm
Non-dominated Sorting Genetic Algorithm version 2
(NSGA-II)
Solution Representation
a vector of offset values: o0=0, o1=5, o2=5, o3=0
Search operators
Selection: Binary tournament selection with replacement
Crossover: uniform cross over
Mutation:
o0=0, o1=5, o2=5, o3=0 à o0=0, o1=5, o2=10, o3=0
Fitness Functions
max CPU time usage per time slot, and
number of time slots during which the tasks run

14. 14
Case Study and Experiments
An automotive software project with 430
tasks.
These 430 tasks can be scheduled in almost
10^320 different ways.

15. 15
Naïve execution of the runnables
5.34ms 5.34ms
5 ms
Time
CPU time usage (ms)
CPU time usage exceeds the size of the slot (5ms)

16. 16
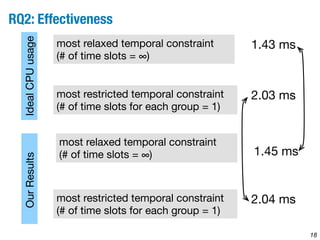
After applying our work
5 ms
ms)
(usage [2.04ms … 1.45ms]
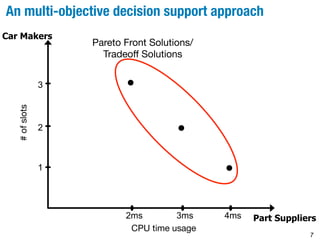
time CPU Time Depending on the number of slots, CPU time usage is
between 2.04ms to 1.45ms. So, around 60% to 70% of
each time slot is guaranteed to be free.

17. 17
Research Questions
RQ1 Sanity Check
Do we do better than a trivial (random search)
solution?
RQ2 Effectiveness
Are we able to find solutions that are close to
known lower bounds?
RQ3 Performance
How long does it take to compute solutions?
RQ4 Usefulness
Are we able to find useful trade-off solutions?

18. 18
RQ2: Effectiveness
most relaxed temporal constraint
(# of time slots = ∞)
most restricted temporal constraint
(# of time slots for each group = 1)
1.43 ms
2.03 ms
most relaxed temporal constraint
(# of time slots = ∞)
1.45 ms
most restricted temporal constraint
(# of time slots for each group = 1)
2.04 ms
Our Results Ideal CPU usage

19. 19
RQ3: Performance
Our approach generates optimal results in about
5 min
90 80
min)
(Time 70
60
50
40
NSGA-II(25,000) Random(25,000)
Time (min)
8
7
6
5
4
NSGA-II(250,000) Random(250,000)

20. 20
RQ4: Usefulness
# of slots
1.452.04
CPU time usage (ms)
21
14
12
1.56
1
2
3
Boundary Trade Offs
Interesting
Solutions

21. Related Work
• Feasibility analysis
– Schedulable or not?
v We perform optimization by finding the best solutions among all
the feasible ones
• Logical models
– Correct/incorrect?
v We provide an explicit time model enabling us to perform a
quantitative analysis
• Symbolically represent the model and rely on model-checkers or
constraint solvers
– State explosion problem
v We scale to very large search spaces: 10^320
21

22. Our Contributions
22
Casting a schedulability analysis problem as a
multi-objective constrained optimization problem
Objective Functions
Constraint models
Search Space
Scaling to a very large industry case study
Search Space of 10^320
Our approach is applicable to similar CPU
utilization problems if
Tasks timing properties are known although tasks may
come from third parties
A constraint model capturing the scheduling policy can
be defined