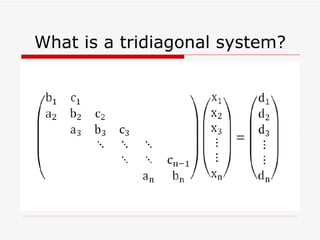
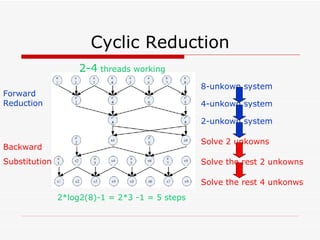
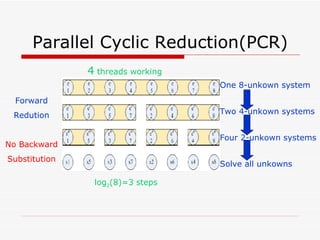
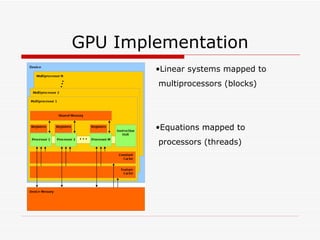
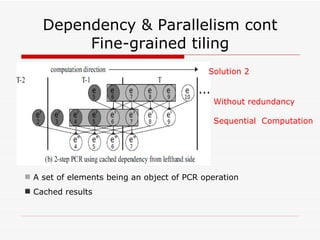
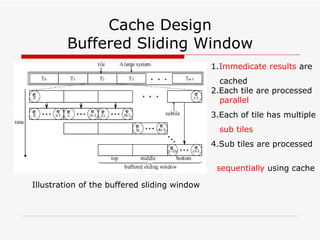
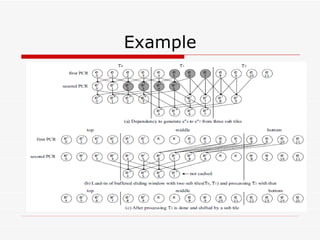
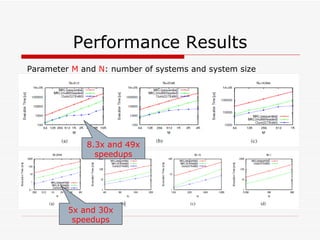
This document summarizes algorithms for solving tridiagonal systems on GPUs. It introduces classic serial and parallel algorithms like Gaussian elimination and cyclic reduction. It then presents a hybrid tiled parallel cyclic reduction (TPCR) algorithm that minimizes redundant memory access through caching. The TPCR algorithm is implemented and tested on a GPU, achieving speedups of 8.3x-49x over a CPU. Factors like cache size, memory access, and synchronization overhead determine the TPCR algorithm's performance.

1. A Scalable Tridiagonal Solver For GPUs Team:WenMin Xiao&ChaoQun Li Institute of information science and technology of Hunan University

2. Outline Introduction Algorithms Classic algorithms Design algorithm for gpu architecture Performance Summary

3. What is a tridiagonal system?

4. What is it used for? Scientific and engineering application Numerical ocean models Semi-coarsening for multi-grid solvers Spectral Poisson Solvers Cubic Spline Approximation Video and computer-animated films Depth of field blurs Fluid simulation

5. Two Applications on GPU Depth of field blur, Michael Kass et al. Shallow water simulation OpenGL and Shader language CUDA Cyclic reduction Cyclic reduction 2006 2007

6. A Classic Serial Algorithm Gussian elimination in tridiagonal case(Thomas algorithm) Phase 1:Forword Reduction Phase 2:Backward Substitution Elimination steps? Complexity? 2n-1 O(n)=2(n-1)+1

7. Parallel Algorithms Coarse-grained algorithms(multi-core CPU) Two-way Gussian elimination Sub-structing method Fine-grained algorithms (many-core GPU) Cyclic Reduction (CR) Parallel Cyclic Reduction (PCR) Recursive Doubling (RD) Hybrid Thomas-PCR algorithm A set of equations mapped to one thread A single equation mapped to one thread

8. Cyclic Reduction 2-4 threads working Forward Reduction Backward Substitution 8-unkown system 4-unkown system 2-unkown system Solve 2 unkowns Solve the rest 2 unkowns Solve the rest 4 unkonws 2*log2(8)-1 = 2*3 -1 = 5 steps

9. Parallel Cyclic Reduction(PCR) Forward Redution No Backward Substitution One 8-unkown system Two 4-unkown systems Four 2-unkown systems Solve all unkowns 4 threads working log 2 (8)=3 steps

10. Advantages of Previous Algorithms Thoms It is easy to parallel solve the independent system CR Every step we reduce the system by half PCR Fewer steps required

11. Hybird Algorithm Improved PCR(Tiled PCR) P-Thomas One 8-unkown system One PCR step Parallel Thomas

12. GPU Implementation Linear systems mapped to multiprocessors (blocks) Equations mapped to processors (threads)

13. Tiled PCR A variant of incomplete PCR in a sense that it stops breaking down the system before the algorithm reaches the smallest possible matrics Redundancy of naive tiling of PCR Redundancy Anthor type of Redundancy K-step PCR: the number of redundant memory access per tile boundary

14. Dependency & Parallelism How to Reduce Redundancy? A set of elements being an object of PCR operation Cached results Solution 1 Redundancy is also exist!

15. Dependency & Parallelism cont Fine-grained tiling A set of elements being an object of PCR operation Cached results Solution 2 Without redundancy Sequential Computation

16. Cache Design Buffered Sliding Window Illustration of the buffered sliding window 1. Immedicate results are cached 2.Each tile are processed parallel 3.Each of tile has multiple sub tiles 4.Sub tiles are processed sequentially using cache

17. Components of Buffered Sliding Window Bottom buffer The input element are just loaded from global memory and ready to be processed Middle buffer mostly interacts with the elements in the bottom by providing denpendency to them at the same time referring them Top buffer caches elements from the middle buffer for the last step of PCR

18. Example

19. Advantages of TPCR Fewer steps Better memory latency hiding(less idle time of GPU execution) Minimizing redundant global memory access Arbitrary tiling size

20. Thread-level Parallel Thomas Algorithm Solves multiple independent system that each thread solves a different system Global memory should be coalesced 64B aligned segment 128B aligned segment

21. Performance Evaluation Test-Platform Nvidia GTX480 GPU with 1.5GB memory bandwith 3.33GHZ Intel quad-core i7 975 CPU Fedora 12 Linux CUDA 3.2

22. Performance Results Parameter M and N : number of systems and system size 8.3x and 49x speedups 5x and 30x speedups

23. Performance Analysis Factors that determine performance Size of intermeidate results cache Global/shared memory access Overhead for synchronization Bank conflick

24. Summary We studied 3 kinds of algorithm for addressing tridiagonal solver We learned Sophisticatedly designed tiling and the buffer sliding window in TPCR algorithm

25. Reference http:// en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm Fast Tridiagonal Solvers on GPU CUDA Programming Guide 高性能运算之 CUDA

26. Question? Thanks