1. DANIEL FERNANDO RODRIGUEZ INGENIERIA DE PETROLEOS ROOTS OF EQUATIONS EXAMPLE

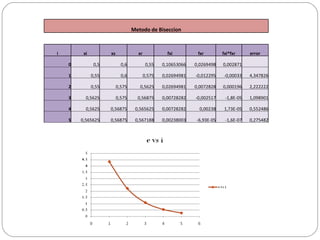
2. Metodo de Biseccion i xi xs xr fxi fxr fxi*fxr error 0 0,5 0,6 0,55 0,10653066 0,0269498 0,002871 1 0,55 0,6 0,575 0,02694981 -0,012295 -0,00033 4,347826 2 0,55 0,575 0,5625 0,02694981 0,0072828 0,000196 2,222222 3 0,5625 0,575 0,56875 0,00728282 -0,002517 -1,8E-05 1,098901 4 0,5625 0,56875 0,565625 0,00728282 0,00238 1,73E-05 0,552486 5 0,565625 0,56875 0,567188 0,00238003 -6,93E-05 -1,6E-07 0,275482

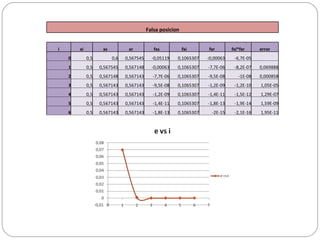
3. Falsa posicion i xi xs xr fxs fxi fxr fxi*fxr error 0 0,5 0,6 0,567545 -0,05119 0,1065307 -0,00063 -6,7E-05 1 0,5 0,567545 0,567148 -0,00063 0,1065307 -7,7E-06 -8,2E-07 0,069888 2 0,5 0,567148 0,567143 -7,7E-06 0,1065307 -9,5E-08 -1E-08 0,000858 3 0,5 0,567143 0,567143 -9,5E-08 0,1065307 -1,2E-09 -1,2E-10 1,05E-05 4 0,5 0,567143 0,567143 -1,2E-09 0,1065307 -1,4E-11 -1,5E-12 1,29E-07 5 0,5 0,567143 0,567143 -1,4E-11 0,1065307 -1,8E-13 -1,9E-14 1,59E-09 6 0,5 0,567143 0,567143 -1,8E-13 0,1065307 -2E-15 -2,1E-16 1,95E-11

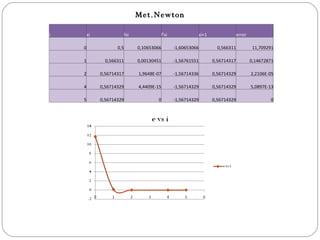
4. Met.Newton i xi fxi f'xi xi+1 error 0 0,5 0,10653066 -1,60653066 0,566311 11,709291 1 0,566311 0,00130451 -1,56761551 0,56714317 0,14672871 2 0,56714317 1,9648E-07 -1,56714336 0,56714329 2,2106E-05 4 0,56714329 4,4409E-15 -1,56714329 0,56714329 5,0897E-13 5 0,56714329 0 -1,56714329 0,56714329 0

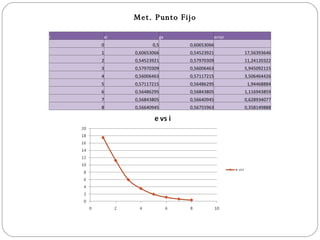
5. Met. Punto Fijo i xi gx error 0 0,5 0,60653066 1 0,60653066 0,54523921 17,56393646 2 0,54523921 0,57970309 11,24120322 3 0,57970309 0,56006463 5,945092115 4 0,56006463 0,57117215 3,506464426 5 0,57117215 0,56486295 1,94468884 6 0,56486295 0,56843805 1,116943859 7 0,56843805 0,56640945 0,628934077 8 0,56640945 0,56755963 0,358149888

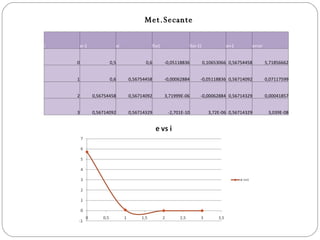
6. Met.Secante i xi-1 xi f(xi) f(xi-1) xi+1 error 0 0,5 0,6 -0,05118836 0,10653066 0,56754458 5,71856662 1 0,6 0,56754458 -0,00062884 -0,05118836 0,56714092 0,07117599 2 0,56754458 0,56714092 3,71999E-06 -0,00062884 0,56714329 0,00041857 3 0,56714092 0,56714329 -2,701E-10 3,72E-06 0,56714329 3,039E-08