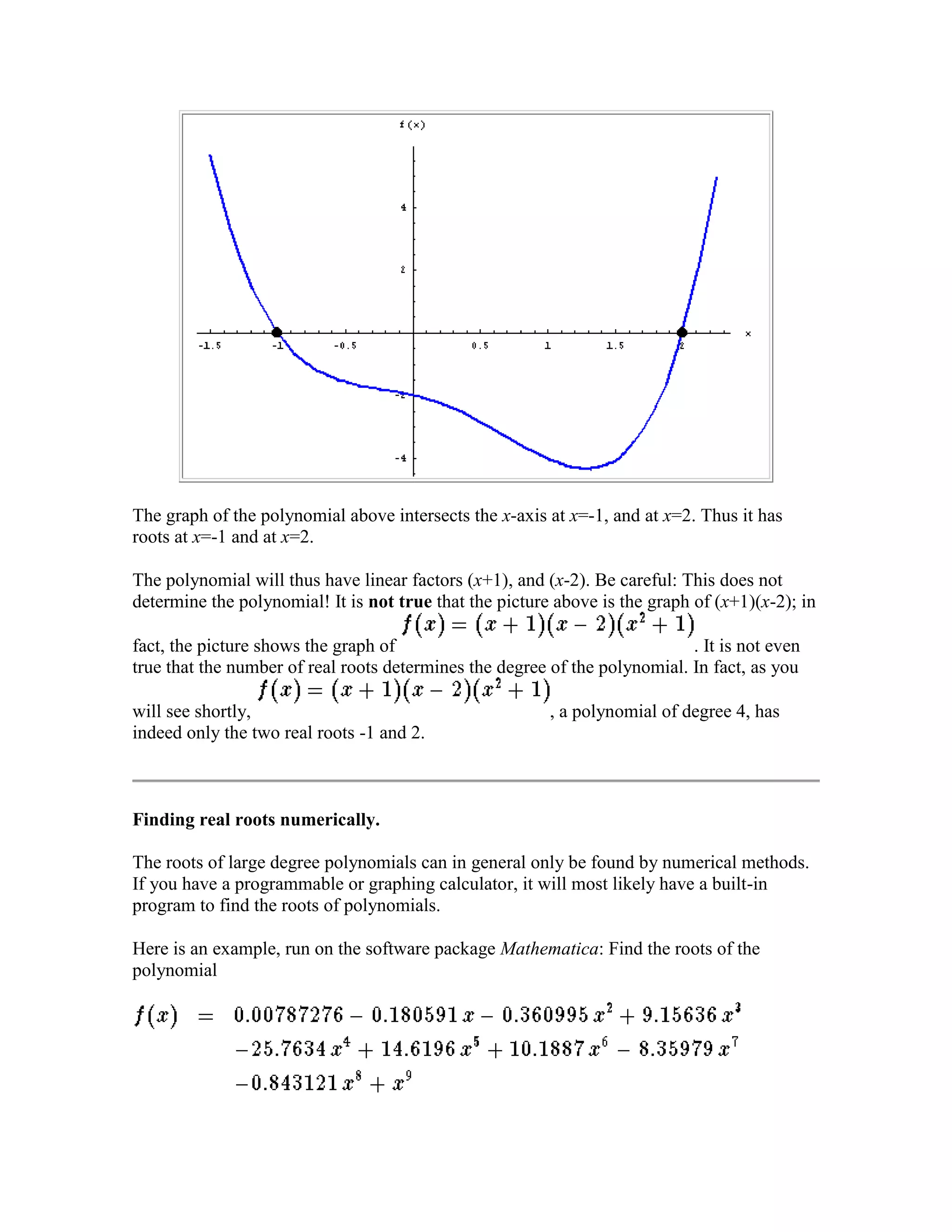
Factoring polynomials breaks them down into simpler factors whose degrees add up to the original polynomial's degree. A number is a root of a polynomial if plugging it into the polynomial equals zero. There is a relationship between roots and factors: if x-a is a factor, then a is a root, and vice versa. Graphically, roots are the x-intercepts of a polynomial's graph. Numerically, programs can find approximations of roots, but may be imprecise.

1. Factoring and Roots of Polynomials
What is factoring?
If you write a polynomial as the product of two or more polynomials, you have factored
the polynomial. Here is an example:
The polynomials x-3 and are called factors of the polynomial
. Note that the degrees of the factors, 1 and 2, respectively, add up
to the degree 3 of the polynomial we started with. Thus factoring breaks up a complicated
polynomial into easier, lower degree pieces.
We are not completely done; we can do better: we can factor
We have now factored the polynomial into three linear (=degree 1) polynomials. Linear
polynomials are the easiest polynomials. We can't do any better. Whenever we cannot
factor any further, we say we have factored the polynomial completely.
Roots of polynomials.
An intimately related concept is that of a root, also called a zero, of a polynomial. A
number x=a is called a root of the polynomial f(x), if
Once again consider the polynomial
Let's plug in x=3 into the polynomial.

2. Consequently x=3 is a root of the polynomial . Note that (x-3) is a
factor of .
Let's plug in into the polynomial:
Thus, is a root of the polynomial . Note that
is a factor of .
Roots and factoring.
This is no coincidence! When an expression (x-a) is a factor of a polynomial f(x), then
f(a)=0.
Since we have already factored
there is an easier way to check that x=3 and are roots of f(x), using the right-
hand side:
Does this work the other way round? Let's look at an example: consider the polynomial
. Note that x=2 is a root of f(x), since

3. Is (x-2) a factor of ? You bet! We can check this by using long
polynomial division:
So we can factor
Let's sum up: Finding a root x=a of a polynomial f(x) is the same as having (x-a) as a linear
factor of f(x). More precisely:
Given a polynomial f(x) of degree n, and a number a, then
if and only if there is a polynomial q(x) of degree n-1 so that
Finding Roots of Polynomials Graphically
and Numerically
Finding real roots graphically.
The real number x=a is a root of the polynomial f(x) if and only if

4. When we see a graph of a polynomial, real roots are x-intercepts of the graph of f(x).
Let's look at an example:
The graph of the polynomial above intersects the x-axis at (or close to) x=-2, at (or close to)
x=0 and at (or close to) x=1. Thus it has roots at (or close to) x=-2, at (or close to) x=0 and
at (or close to) x=1.
The polynomial will also have linear factors (x+2), x and (x-1). Be careful: This does not
determine the polynomial! It is not true that the picture above is the graph of (x+2)x(x-1);
in fact, the picture shows the graph of f(x)=-.3(x+2)x(x-1).
Here is another example:

5. The graph of the polynomial above intersects the x-axis at x=-1, and at x=2. Thus it has
roots at x=-1 and at x=2.
The polynomial will thus have linear factors (x+1), and (x-2). Be careful: This does not
determine the polynomial! It is not true that the picture above is the graph of (x+1)(x-2); in
fact, the picture shows the graph of . It is not even
true that the number of real roots determines the degree of the polynomial. In fact, as you
will see shortly, , a polynomial of degree 4, has
indeed only the two real roots -1 and 2.
Finding real roots numerically.
The roots of large degree polynomials can in general only be found by numerical methods.
If you have a programmable or graphing calculator, it will most likely have a built-in
program to find the roots of polynomials.
Here is an example, run on the software package Mathematica: Find the roots of the
polynomial

6. Using the "Solve" command, Mathematica lists approximations to the nine real roots as
Here is another example, run on Mathematica: Find the roots of the polynomial
Mathematica lists approximations to the seven roots as
Only one of the roots is real, all the other six roots contain the symbol i, and are thus
complex roots (more about those later on). Note that the complex roots show up "in pairs"!
Numerical programs usually find approximations to both real and complex roots.
Numerical methods are error-prone, and will get false answers! They are good for
checking your algebraic answers; they also are a last resort if nothing else "works".