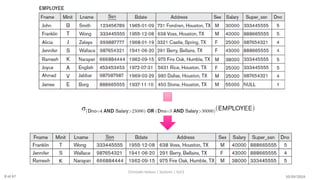
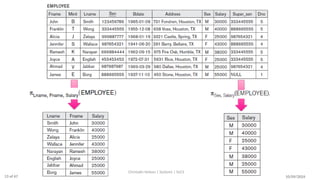
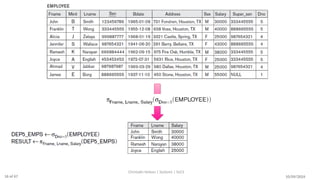
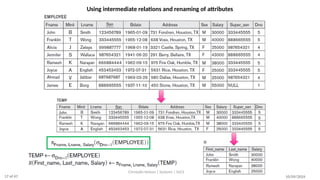
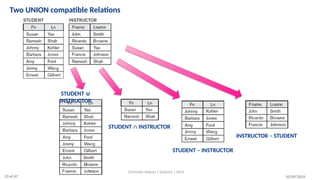
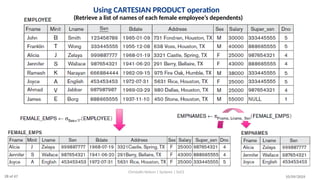
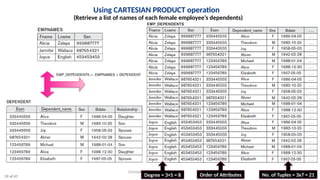
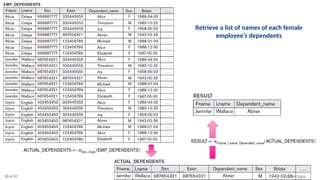
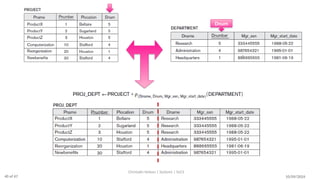
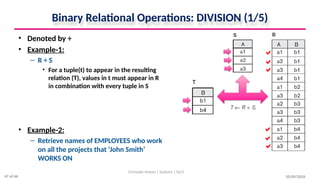
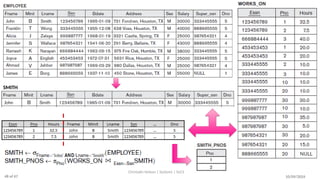
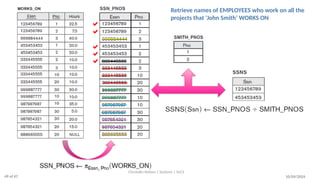
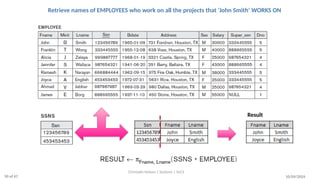
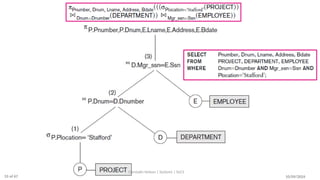
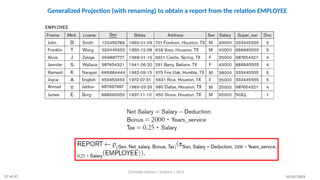
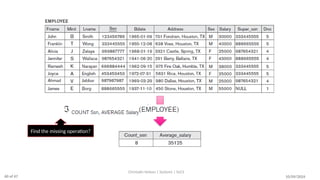
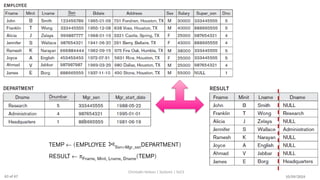
The document discusses formal languages related to relational databases, focusing on relational algebra and relational calculus, highlighting their expressive power and relationships. It covers unary and binary relational operations, including select, project, join, and various set theory operations, while explaining their procedural nature and how they relate to SQL. Additionally, it details types of joins and operations applicable to relations, emphasizing practical applications and examples.