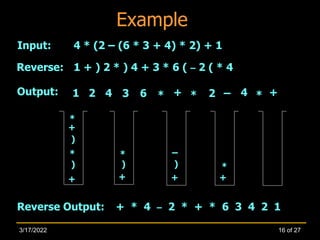
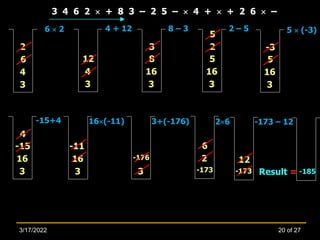
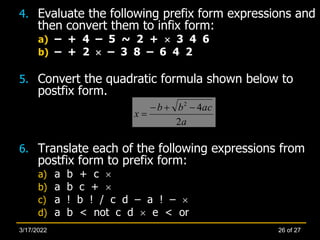
The document discusses the application of stacks in converting arithmetic expressions into different notations (infix, prefix, postfix). It highlights the importance of operator precedence, parenthesis, and the use of polish and reverse polish notations for efficient evaluation. Furthermore, it includes methods for converting between notations and exercises for practice.

1. Application of Stacks
By
S. Christalin Nelson

2. Formula Translation
 The Problem: Writing formula or arithmetic
expressions in something close to their usual
mathematical/scientific form
 One of the most important accomplishments of early
design computer languages in designing a compiler that
understood expressions & to produce a machine-
language output.
 In fact, the name FORTRAN stands for FORMULA
TRANSLATOR.
2 of 27
3/17/2022

3. The Quadratic formula
x = (-b + (b*b – (4*a)*c)^0.5) / (2*a)
Question
 Which operation must be done before others?
 What are the effects of the parentheses? When
can they omitted?
 How many times you will look back and forth
through the expression until you evaluate it?
a
ac
b
b
x
2
4
2




3 of 27
3/17/2022

4. Compiler Conventions
 Parenthesis has highest priority
 Few important Priorities
1. unary
2. ^
3. * /
4. + –
4 of 27
3/17/2022

5. Operator priority & associativity
Binary operators
1. * / %
2. + –
3. < <= > >=
4. == !=
5. &&
6. ||
7. =
Unary operators
 -5
 +5
 + –5 = –5
 – –5 = 5
5 of 27
3/17/2022

6. Polish Notation
 Discovered by the polish mathematician
Jan Lukasiewicz.
 Expressions can be classified w.r.t. the
position of its Operators among operands
 Before operand(s)  prefix expression
 After operand(s)  postfix expression
 In-between operands  infix expression
6 of 27
3/17/2022

7. Polish & Reverse Polish Notations
Infix: a  b
prefix   a b
postfix  a b 
Infix: a + b  c
prefix  + a  b c
postfix  a b c  +
Prefix and Postfix are not
mirror to each other
Prefix (Polish)
Postfix (Reverse Polish)
7 of 27
3/17/2022

8. Polish Notation - Importance
 Infix Expressions are harder for Computers to
evaluate because of the additional work needed
to decide on precedence. Hence conversion to
Polish or Reverse Polish Notation is required.
 It is not necessary to make repeated scans
through the expression
 Use of parentheses (if required)
 Evaluation can be achieved with great efficiency
8 of 27
3/17/2022

9. Activity -1 (Self-Test)
 Change the following expression to
a) Reverse Polish notation
b) Polish notations
3 + (4 + 6  2)  ((8 – 3)  (2 - 5) + 4) – 2  6
a) Reverse Polish Notation:
3 4 6 2  + 8 3 – 2 5 –  4 +  + 2 6  –
b) Polish Notation:
– + 3  + 4  6 2 +  – 8 3 – 2 5 4  2 6
9 of 27
3/17/2022

10.  Evaluate the following expressions
5 4  Error
6   Error
+  Error
5 –   Unary operator
Reverse Polish Notation
Note:
• Use different symbol to represent unary operator i.e. (~)
• Example: Convert to Reverse Polish
(-5) – (-4)  (~5) – (~4)  5 ~ 4 ~ –
10 of 27
3/17/2022

11. Converting Infix to Postfix with Stack
 Read expression from Left-to-Right and
 if an operand is read copy it to the output,
 if a left parenthesis is read push it into the stack,
 when a right parenthesis is encountered, the operator at the top of
the stack is popped off the stack and copied to the output until the
symbol at the top of the stack is a left parenthesis. When that occurs,
both parentheses are discarded,
 if an operator is scanned and has a higher precedence than the
operator at the top of the stack, the operator being scanned is pushed
onto the stack,
 while the precedence of the operator being scanned is lower than or
equal to the precedence of the operator at the top of the stack, the
operator at the top of the stack is popped and copied to the output,
 when the end of the expression is reached on the input scan, the
remaining operators in the stack are popped and copied to the output.
11 of 27
3/17/2022

12. Example
*
(
–
(
*
Input: 4 * (2 – (6 * 3 + 4) * 2) + 1
Output:
*
(
–
(
+
*
(
–
*
*
4 2 6 3 * 4 + 2 * – *
+
1 +
12 of 27
3/17/2022

13. Converting Infix to Prefix with Stack
1st method
 Read expression from Right-to-Left and
 if an operand is read copy it to the RIGHT of the output,
 if a right parenthesis is read push it into the stack,
 when a left parenthesis is encountered, the operator at the top of the
stack is popped off the stack and copied to the output until the
symbol at the top of the stack is a right parenthesis. When that
occurs, both parentheses are discarded,
 if an operator is scanned and has a higher or equal precedence than
the operator at the top of the stack, the operator being scanned is
pushed onto the stack,
 while the precedence of the operator being scanned is lower than to
the precedence of the operator at the top of the stack, the operator at
the top of the stack is popped and copied to the output,
 when the end of the expression is reached on the input scan, the
remaining operators in the stack are popped and copied to the LEFT
of the output.
13 of 27
3/17/2022

14. Example
+
)
*
)
+
Input: 4 * (2 – (6 * 3 + 4) * 2) + 1
Output:
–
*
+ * 4 – 2 * + * 6 4 2 1
3
+
)
*
+
)
+
*
14 of 27
3/17/2022

15. Converting Infix to Prefix with Stack
2nd method
 Reverse the expression & Read expression from Left-to-Right
 if an operand is read copy it to the output (left-to-right)
 if a right parenthesis is read push it into the stack
 when a left parenthesis is encountered, the operator at the top of the
stack is popped off the stack and copied to the output until the
symbol at the top of the stack is a right parenthesis. When that
occurs, both parentheses are discarded.
 if an operator is scanned and has a higher or equal precedence than
the operator at the top of the stack, the operator being scanned is
pushed onto the stack
 while the precedence of the operator being scanned is lower than to
the precedence of the operator at the top of the stack, the operator at
the top of the stack is popped and copied to the output
 when the end of the expression is reached on the input scan, the
remaining operators in the stack are popped and copied to the output.
 Reverse the output
15 of 27
3/17/2022

16. Example
+
)
*
)
+
Input: 4 * (2 – (6 * 3 + 4) * 2) + 1
Output:
–
*
+
*
4
–
2
*
+
*
6
4
2
1 3
+
)
*
+
)
+
*
1 + ) 2 * ) 4 + 3 * 6 ( – 2 ( * 4
Reverse:
+ * 4 – 2 * + * 6 3 4 2 1
Reverse Output:
16 of 27
3/17/2022

17. Activity-2
 Using stack diagrams convert the following
expressions into postfix and prefix forms of polish
notation:
a) 8 – 3  4 + 2
b) 8 – 3  (4 + 2)
c) (8 – 3)  (4 + 2)
d) (8 – 3)  4 + 2
e) (-a + b)  (c + a) – 5
f) 2 + ((-3 + 1)  (4 – 2) + 3)  6 – (1 + 2  3)
g) (5 > 4) and not (3 = 2 – 1)
17 of 27
3/17/2022

18. Activity-2 (Solution)
Infix Rev. Polish Polish
8 – 3  4 + 2 8 3 4 x - 2 + - 8 + x 3 4 2
8 – 3  (4 + 2) 8 3 4 2 + x - - 8 x 3 + 4 2
(8 – 3)  (4 + 2) 8 3 - 4 2 + x x - 8 3 + 4 2
(8 – 3)  4 + 2 8 3 - 4 x 2 + + x - 8 3 4 2
(-a + b)  (c + a) – 5 a ~ b + c a + x 5 - ?
2 + ((-3 + 1)  (4 – 2) + 3)  6 – (1 + 2  3) ? ?
(5 > 4) && !(3 = 2 – 1) ? ?
18 of 27
3/17/2022

19. Evaluation of Reverse Polish
Expressions
 Most compilers use the polish form to translate
expressions into machine language.
 Evaluation is done using a stack data-structure
 Read expression from left to right and build the stack of
numbers (operands).
 When an operator is read two operands are popped out
of the stack they are evaluated with the operator and the
result is pushed into the stack.
 At the end of the expression there must be only one
operand into the stack (the solution) otherwise ERROR.
19 of 27
3/17/2022

20. 5
3
3 4 6 2  + 8 3 – 2 5 –  4 +  + 2 6  –
3
4
6
2
6  2
3
4
12
4 + 12
3
16
8
8 – 3
2
3
16
5
2 – 5
-3
3
16
5
5  (-3)
4
3
16
-15
-15+4
3
16
-11
16(-11)
3
-176
3+(-176)
-173
2
6
26
-173
12
-173 – 12
-185
Result =
20 of 27
3/17/2022

21. Evaluation of Polish Expressions
 Evaluation is done using a stack data-structure
 Read expression from right to left and build the stack of
numbers (operands).
 When an operator is read two operands are popped
out of the stack they are evaluated with the operator
and the result is pushed into the stack.
 At the end of the expression there must be only one
operand into the stack (the solution) otherwise ERROR.
21 of 27
3/17/2022

22. 3
–  3 – 8  3 2 – ~ 4 – 6 2
2
6
6 – 2
4
4
-4
4
-4
-4 – 4
2
-8
3  2
6
-8
8
8 – 6
3
-8
2
3  2
-8
6
6 – (-8)
14
Result =
22 of 27
3/17/2022

23. Running-sum condition
 For a sequence E of operands, unary operators and
binary operators, form a running-sum by starting at
the left-end of E and counting
 +1 for each operand,
 0 for unary operator, and
 –1 for each binary operator.
 E satisfies the running-sum condition provided that
it never falls below 1, and is exactly 1 at the right-
hand-end of E.
3 4 6 2  + 8 3 – 2 5 –  4 +  + 2 6  –
23 of 27
3/17/2022

24. Exercises
1. Which of the following are syntactically correct
postfix expressions (use the running-sum
condition)? Show the error in each incorrect
expression. Translate each correct expression into
infix form.
a) a b c +  a / c b + d / –
b) a b + c a  b c / d –
c) a b + c a  – c  + b c –
d) a ~ b 
e) a  b ~
f) a b  –
g) a b ~ 
24 of 27
3/17/2022

25. 2. Convert the following postfix form expressions to
infix form:
a) a b + a b – 
b) a b + c 
c) a b c + 
d) a b c + a c d –   b + –
3. Evaluate the following postfix form expressions
and then convert them to infix form:
a) 4 5 2 + 3  –
b) 2 4 6 – 8 3 –  2 + –
25 of 27
3/17/2022

26. 4. Evaluate the following prefix form expressions and
then convert them to infix form:
a) – + 4 – 5 ~ 2 +  3 4 6
b) – + 2  – 3 8 – 6 4 2
5. Convert the quadratic formula shown below to
postfix form.
6. Translate each of the following expressions from
postfix form to prefix form:
a) a b + c 
b) a b c + 
c) a ! b ! / c d – a ! – 
d) a b < not c d  e < or
a
ac
b
b
x
2
4
2




26 of 27
3/17/2022

27. 7. Evaluate the following prefix expressions. Hence,
translate them into postfix form:
a) / + 2 4 ! 4
b) / + ! 3 9 3
c) and < 3 4 or not = + 2 5 7 > 3 0
8. Translate each of the following expressions from
infix form into postfix and then by using stack
diagrams evaluate the postfix expressions:
a) 5 * ((-3 – 2) * (4 – 6) + 3 * 2)
b) -3 + (5 + 2) * 8 + 6 – ((4 – 2 * 3) * (-2 – 3) – 9)
c) 9 + 5 * ((3 + 2) – 8 * (1 – 3) * (-3 – 6)) + 2 * 3
d) 1 – (3 – (-1 + 2 * (6 + 7 * 2)))
27 of 27
3/17/2022