chapter 6 Relational Algebra and calculus.pdf

Fundamentals of Database system
Chapter Six
Relational Algebra and calculus
Prepared by:
Misganaw A, Getnet T, and Agereselam D.
University of Gondar
College Of Informatics
Department of computer science

Outline
 Relational Query Languages
 What is an Algebra?
 Basic Relational Algebra Operations
 Relational Calculus?

Relational Query Languages
 Query languages: Allow manipulation and retrieval of
data from a database.
 Relational model supports simple, powerful QLs:
 Allows for optimization.
 Query Languages != programming languages because
query languages are used to interact with database,
while programming languages are used to develop
software applications.
 QLs not intended to be used for complex calculations.
 QLs support easy, efficient access to large data sets.

…Relational Query Languages
 Two mathematical Query Languages form the basis for
“real” query languages (e.g. SQL), and for implementation,
which is the relational algebra and calculus were
developed before the SQL language
1. Relational Algebra: More operational, very useful for
representing execution plans.
 Basis for SEQUEL (Structured English query language later
shortened SQL)
2. Relational Calculus: Let’s users describe WHAT they
want, rather than HOW to compute it. (Non-
operational, declarative.)
 Basis for QUEL (based on tuple relational calculus)

What is an Algebra?
 Mathematical system consisting of:
– Operands --- variables or values from which new
values can be constructed.
– Operators --- symbols denoting procedures that
construct new values from given values.
 A table is a mathematical relation. Which have the
Synonyms:
– Table = relation
– Row (record) = tuple
– Column (field) = attribute

…What is Algebra
 An algebra whose operands are relations or variables
that represent relations.
 Operators are designed to do the most common things
that we need to do with relations in a database.
 The result is an algebra that can be used as a query
language for relations.
 A collection of operations that users can perform on
relations to obtain a desired result.
 For each operation: both the operands and the result are
relations

…What is Algebra
 Relational algebra is a procedural query language, which
takes instances of relations as input and yields instances of
relations as output. It uses operators to perform queries.
 An operator can be either unary or binary. They accept
relations as their input and yield relations as their output.
 Relational algebra is performed recursively on a relation
and intermediate results are also considered relations.

Basic Relational Algebra Operations
 unary operations: Unary operations take as input a single table and
produce as output another table.
– Selection ( σ ): Selects a subset of tuples from a relation.
– Projection ( π ): Selects columns from a relation.
– Rename ( ): it used to rename the relation as well as the attributes.
 Binary operations: Binary operations take as input two tables and
produce as output another table.
– Cross-product ( × ): Allows us to combine two relations.
– Set-difference ( - ): Tuples in relation 1, but not in relation 2.
– Union ( ∪ ): Tuples in relation 1 and in relation 2.
– Additional operations: Intersection, join, division : Not essential, but
(very) useful.

• Traditional Set Operation
–
–
–
–
Union
Intersection
Difference
Cartesian product
• Special Operations
–
–
–
–
Selection
Projection
Join
Division
Rename
Or Unary Operators.
Selection :- 
Projection :- 
Rename :- 
Binary Operators.
Product (Cartesian Product) :- 
Union :- 
Difference :- –
Intersection:- 
Join
Division
Relational Algebra operators categories

Unary Operations: Select
 Select produces a table that only contains the tuples that satisfy
a particular condition, in other words a “horizontal” subset.
Selects rows that satisfy the selection condition. No duplicates
in result. Schema of result is identical to schema of input
relation •
 Selection predicates can include: <, >, =, !=, and, or, not
 Appearance(syntax): σC(R):
where σ = Sigma
C is a selection condition and
R is the relation over which the selection takes place

Example of Select
123
345
567
Fred
John
Ann
address
3
6
5
Oxford
Hope Rd.
Garden
300(Student) yields
Hope Rd.
Garden
σ sid>
345
567
John
Ann
6
5
name
sid
Student
address
sid name

SID Name Login DoB GPA
55515 Smith smith@ccs Jan 10,1990 3.82
55516 Jones jones@hist Feb 11, 1992 2.98
55517 Ali ali@math Sep 22, 1989 3.11
55518 Smith smith@math Nov 30, 1991 3.32
EXample2
σ𝑆ID>55516 (S1)
55517 Ali ali@math Sep 22, 1989 3.11
Exercise: 1. σ𝑆ID! =55516 (S1)
2. σ (S1)

Unary Operations: Project
 Project produces a table consisting of only some of the
attributes.
– It creates a “vertical” subset.
 Deletes attributes that are not in projection list.
 Schema of result contains exactly the fields in the projection
list, with the same names that they had in the input relation.
Syntax: ПA(R) where П=Pi
– A is a set of attributes of R
– R is the relation over which the project takes place.
 Projection operator has to eliminate duplicates.

Example of Project
sid
123
234
345
cid
CS51T
CS52S
CS52S
grade
76
50
55
cid
CS51T
CS52S
Enrol
Пcid(Enrol) yields

55517 Ali ali@math Sep 22, 1989 3.11
EXample2
π𝑆ID, Name(S1)
SID Name
55515 Ali
55516 Smith
55517 Ali
55518 Smith
π𝑆ID(S1)
SID
55515
55516
55517
55518

Relational Algebra expression when an Operator
composition example: SELECT AND PROJECT
#query: display the student’s id and students name whose id is greater than 55516
π𝑆ID, Name (σ𝑆ID> 55516 (S1) ))
SID Name
55517 Ali
55518 Smith

Rename Operation
 The renaming operator can be used to explicitly rename resulting relations
of an expression.
– S(A1, A2, … An) (R)
–  represents the RENAME operator,
– S is a name for the new relation , and
– A1, A2, … An are new names for the attributes in the relation R.
 Example-1: Query to rename the relation Student as Male Student and the
attributes of Student – RollNo, SName as (Sno, Name).
Sno Name
2600 Ronny
2655 Raja
ρ MaleStudent(Sno, Name) πRollNo, SName(σCondition(Student))

Binary Operations
 Two relations are (union) compatible If they have the
same set of attributes.
 Example, one table may represent suppliers in one
country, while another table with same schema
represents suppliers in another country.
 For the union, intersection and set- difference
operations, the relations must be compatible.

Union, Intersection, Set- difference
R1 R2
– The union is the
in R1 or R2.
table comprised of all tuples
R1 R2
– The intersection
tuples in R1 and
is the table comprised of
R2
all
R1 - R2
– The set-difference between R1 and R2 is the table
consisting of all tuples in R1 but not in R2.


 Union:
Intersection:
Set-difference:

UNION (U)
 It includes all tuples that are in tables A or in B. It also eliminates duplicate tuples.
For a union operation to be valid, the following conditions must hold
– R and S must be the same number of attributes.
– Attribute domains need to be compatible.
– Duplicate tuples should be automatically removed.
 Example: Consider the following tables.
 S1 S2US1
 S2
55515 Chen chen@ccs Jan 10,1990 3.01
55519 Alton alton@hist Jun 11, 1992 2.07
55517 Ali ali@math Sep 22, 1989 3.11
55517 Ali ali@math Sep 22, 1989 3.11
55516 Jones jones@hist
Feb 11,
1992
2.98
55517 Ali ali@math
Sep 22,
1989
3.11
55518 Smith smith@math
Nov 30,
1991
3.32
55515 Chen chen@ccs Jan 10,1990 3.01
-> Duplicate row are
removed and result is

Intersection (∩)
 Occurs in S1 and S2 S1 ∩ S2
 Defines a relation consisting of a set of all tuple that are in both
A and B. However, A and B must be union-compatible.
 Consider on the above example in the previous slide the
intersection of S1 and S2 is:
S1 ∩S2
55517 Ali ali@math Sep 22, 1989 3.11

Set-Difference (-)
 Occurs in S1 but not in S2 S1 – S2
 Set Difference (-) – Symbol denotes it. The result of A – B, is
a relation which includes all tuples that are in A but not in B
 Example consider in the above example on the the previous
slide given on union example:
 The result of S1-S2 is
55515 Chen chen@ccs Jan 10,1990 3.01

Cartesian Product (X)
 Cartesian Product in DBMS is an operation used to merge columns from
two relations. Each row within R1 is paired with each row of R2, The
syntax is: R1X R2
 Example relation R1XR2:
R1 R1XR2:
R2
CId Grade
History 101 C
Biology 220 A
Anthro 320 B
Music 101 A
SID Name Login DoB GPA CID Grade
55515 Smith smith@ccs Jan 10,1990 3.82 History 101 C
55515 Smith smith@ccs Jan 10,1990 3.82 Biology 220 A
55515 Smith smith@ccs Jan 10,1990 3.82 Anthro 320 B
55515 Smith smith@ccs Jan 10,1990 3.82 Music 101 A
55516 Jones jones@hist Feb 11, 1992 2.98 History 101 C
55516 Jones jones@hist Feb 11, 1992 2.98 Biology 220 A
55516 Jones jones@hist Feb 11, 1992 2.98 Anthro 320 B
55516 Jones jones@hist Feb 11, 1992 2.98 Music 101 A

Example of a Cartesian Product
R1 R1 X R2
R2
A B
1 X
2 Y
C D
a s
b t
c u
A B C D
1 x a s
1 x b t
1 x c U
2 y a s
2 y b t
2 y c U

join operation
 Join operation combines the relation R1 and R2 with respect to a condition.
It is denoted by ⋈.
 Join: A Join operation pairs two tuples from different relations, if and only if
a given join condition is satisfied. The different types of join operation are as
follows −
– Inner join: join only those tuples that satisfy the matching criteria are
included, while the rest are excluded
 Theta join
 Equi join
 Natural join
– Outer join − It is further classified into following types −
 Left outer join.
 Right outer join.
 Full outer join.

Inner join VS outer Join
Inner Join Outer Join

Theta (θ) Join
 If we join R1 and R2 other than the equal to condition then it is called
theta join/ non-equi join with theta condition.
 Example consider R1 table
R1
R2
RegNo Branch Section
1 CSE A
2 ECE B
3 CIVIL A
4 IT B
5 IT A
Name RegNo
Bhanu 2
Priya 4
RegNo Branch Section Name Regno
3 CIVIL A Bhanu 2
4 IT B Bhanu 2
5 IT A Bhanu 2
5 IT B Priya 4
R1 ⋈ θ R2 (θ is R1.regno > R2.regno
R1 ⋈ R1.regno > R2.regno R2
Theta Join uses <, >, <=, or
>=

Equi Join
 EQUI Join: If we join R1 and R2 on equal condition then it is
called equi join.
 Consider the above example the result of equi join from R1
and R2 are
R1 ⋈ R1.regno = R2.regno R2
RegNo Branch Section Name Regno
2 ECE B Bhanu 2
4 IT B Bhanu 2

Natural Join
 Generally, join is referred to as natural join. A natural join is the
set of tuples of all combinations in R and S that are equal on
their common attribute names.
 The resulting table will contain all the attributes of both the
table but keep only one copy of each common column.
 Assume R1 and R2 have attributes A in common. Natural join
is formed by concatenating all tuples from R1 and
concatenating all tuples from R1 and R2 with the same value of
A and dropping the occurrence of A in R2.
R1⋈ R2
R1 R2 = ПA’(C(R1R2))

Example: consider the following relations course
and head of department(HoD) natural join operation
Courses
CID Course Dept
CS01 Database CS
ME01 Mechanics ME
EE01 Electronics EE
HoD
Dept Head
CS Alex
ME Maya
EE Mira
Courses ⋈ HoD
Dept CID Course Head
CS CS01 Database Alex
ME ME01 Mechanics Maya
EE EE01 Electronics Mira

The difference between Natural, Theta, and Equi join
 Natural Join: Natural join can be possible when there is at least
one common attribute in two relations.
 Natural joins automatically join tables based on column names
and eliminate duplicate columns from result
 Theta Join: Theta join can be possible when two act on
particular condition, it uses all comparison operators.
 Equi Join: Equi can be possible when two act on equity
condition. It is one type of theta join.

Outer Joins
 Theta Join, Equijoin, and Natural Join are called inner joins. An
inner join includes only those tuples with matching attributes
and the rest are discarded in the resulting relation.
 Therefore, we need to use outer joins to include all the tuples
from the participating relations in the resulting relation.
 There are three kinds of outer joins − left outer join, right outer
join, and full outer join

Left Outer Join(R S)
 All the tuples from the Left relation, R, are included in the resulting relation.
If there are tuples in R without any matching tuple in the Right relation S,
then the S-attributes of the resulting relation are made NULL.
Left (course)
A B
100 Database
101 Mechanics
102 Electronics
Right (HoD)
A B
100 Alex
102 Maya
104 Mira
Courses HoD
A B C D
100 Database 100 Alex
101 Mechanics --- ---
102 Electronics 102 Maya

Right Outer Join: ( R S )
 All the tuples from the Right relation, S, are included in the resulting
relation. If there are tuples in S without any matching tuple in R, then the R-
attributes of resulting relation are made NULL.
 Consider the above example(previous slid the right outer join result for
course and head of department(HoD) is:
Courses HoD
A B C D
--- --- 104 Mira

Full Outer Join: ( R S)
 All the tuples from both participating relations are included in
the resulting relation. If there are no matching tuples for both
relations, their respective unmatched attributes are made
NULL.
Courses HoD
A B C D
101 Mechanics --- ---
--- --- 104 Mira

Relational Calculus:
 Before understanding Relational calculus in DBMS, we need to
understand Procedural Language and Declarative Langauge.
 Procedural Language - Those Languages which clearly define how to get
the required results from the Database are called Procedural
Language. Relational algebra is a Procedural Language.
 Declarative Language - Those Language that only cares about What to get
from the database without getting into how to get the results are called
Declarative Language.
 Relational Calculus is a Declarative Language. So Relational Calculus is a
Declarative Language that uses Predicate Logic or First-Order Logic to
determine the results from Database.

…cont
 There is an alternate way of formulating queries known as
Relational Calculus. Relational calculus is a non-procedural
query language.
 In the non-procedural query language, the user is concerned
with the details of how to obtain the end results.
 The relational calculus tells what to do but never explains how
to do.
 Most commercial relational languages are based on aspects of
relational calculus including SQL-QBE and QUEL.

Relational Calculus?
 It is based on Predicate calculus, a name derived from branch of symbolic
language. A predicate is a truth-valued function with arguments. On
substituting values for the arguments, the function result in an expression
called a proposition.
 It can be either true or false. It is a tailored version of a subset of the Predicate
Calculus to communicate with the relational database.
 Many of the calculus expressions involves the use of Quantifiers. There
are two types of quantifiers:
– Universal Quantifiers: The universal quantifier denoted by ∀ is read as for all
which means that in a given set of tuples exactly all tuples satisfy a given
condition.
– Existential Quantifiers: The existential quantifier denoted by ∃ is read as for all
which means that in a given set of tuples there is at least one occurrences whose
value satisfy a given condition.

TYPES OF Relational Calculus
 Relational Calculus is of Two Types:
– Tuple Relational Calculus (TRC)
– Domain Relational Calculus (DRC)
1. Tuple Relational Calculus (TRC)
– Tuple Relational Calculus in DBMS uses a tuple variable (t) that goes to
each row of the table and checks if the predicate is true or false for the
given row.it is used for selecting those tuples that satisfy the given
conditions.
– Notation: A Query in the tuple relational calculus is expressed as
following notation {T | P (T)} or {T | Condition (T)} read as a
set of all tuples of T such that predicate p is true for T
Where
T is the resulting tuples
P(T) is the condition used to fetch T.

 For example:
– { T.name | Author(T) AND T.article = 'database' }
– Output: This query selects the tuples from the AUTHOR relation. It returns a
tuple with 'name' from Author who has written an article on 'database'.
 TRC (tuple relation calculus) can be used logical operators or
quantified. Quantifiers In TRC, we can use Existential (∃) and
Universal Quantifiers (∀).
 For example:
– { R| ∃T ∈ Authors(T.article='database' AND R.name=T.name)}
– Output: This query will yield the same result as the previous one.

example
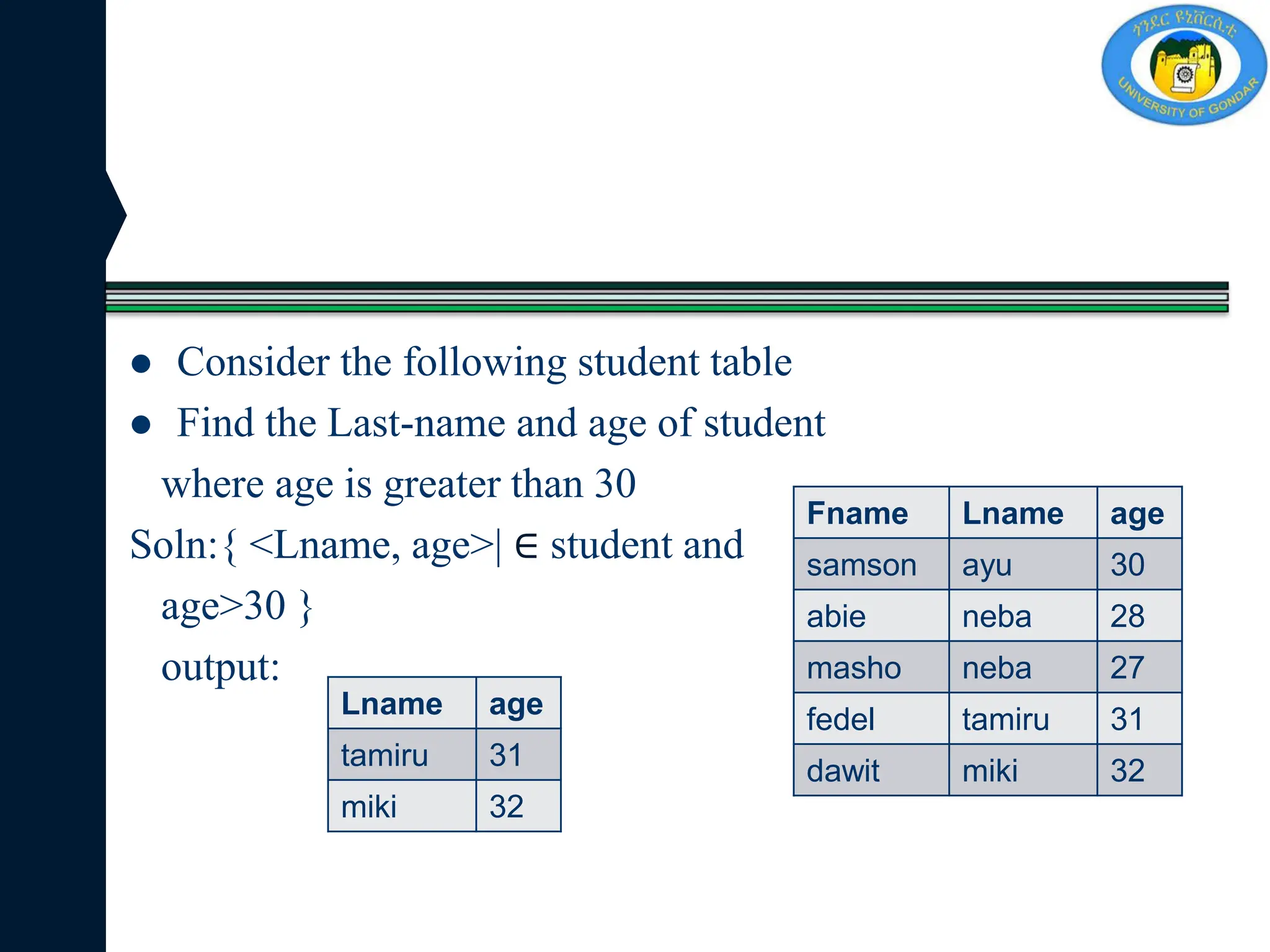
 Find the branch-name, loan-number and amount for loan over 150
 { t/t Є loan ᴧ t[amout]>1500 }
 Find the loan-number for each loan of an amount grater than 150
– Here there is projection and selection
 { t| ⱻ L Є loan(t[loan-number]=L[loan-number] ᴧ L[amount]>150}
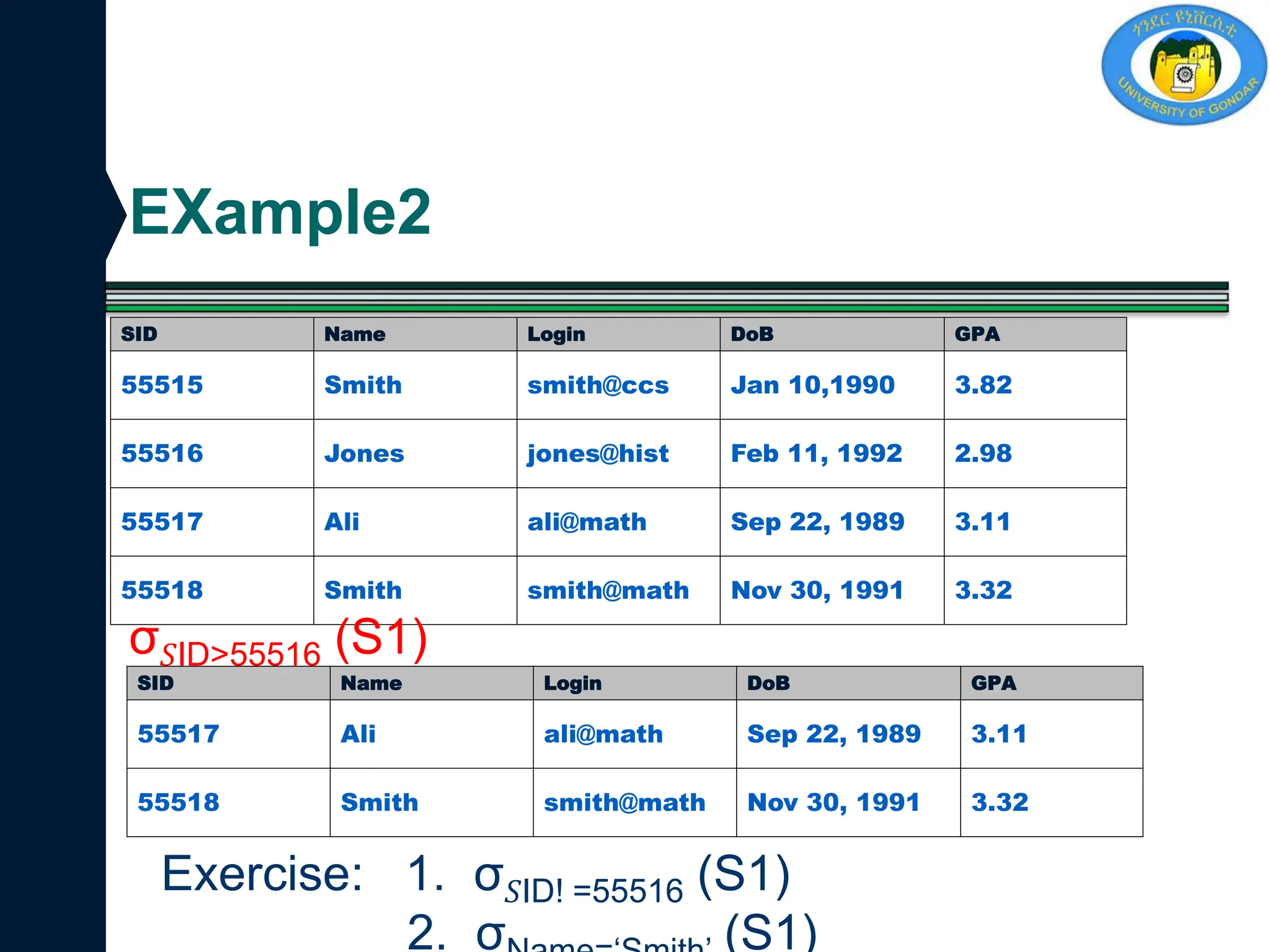
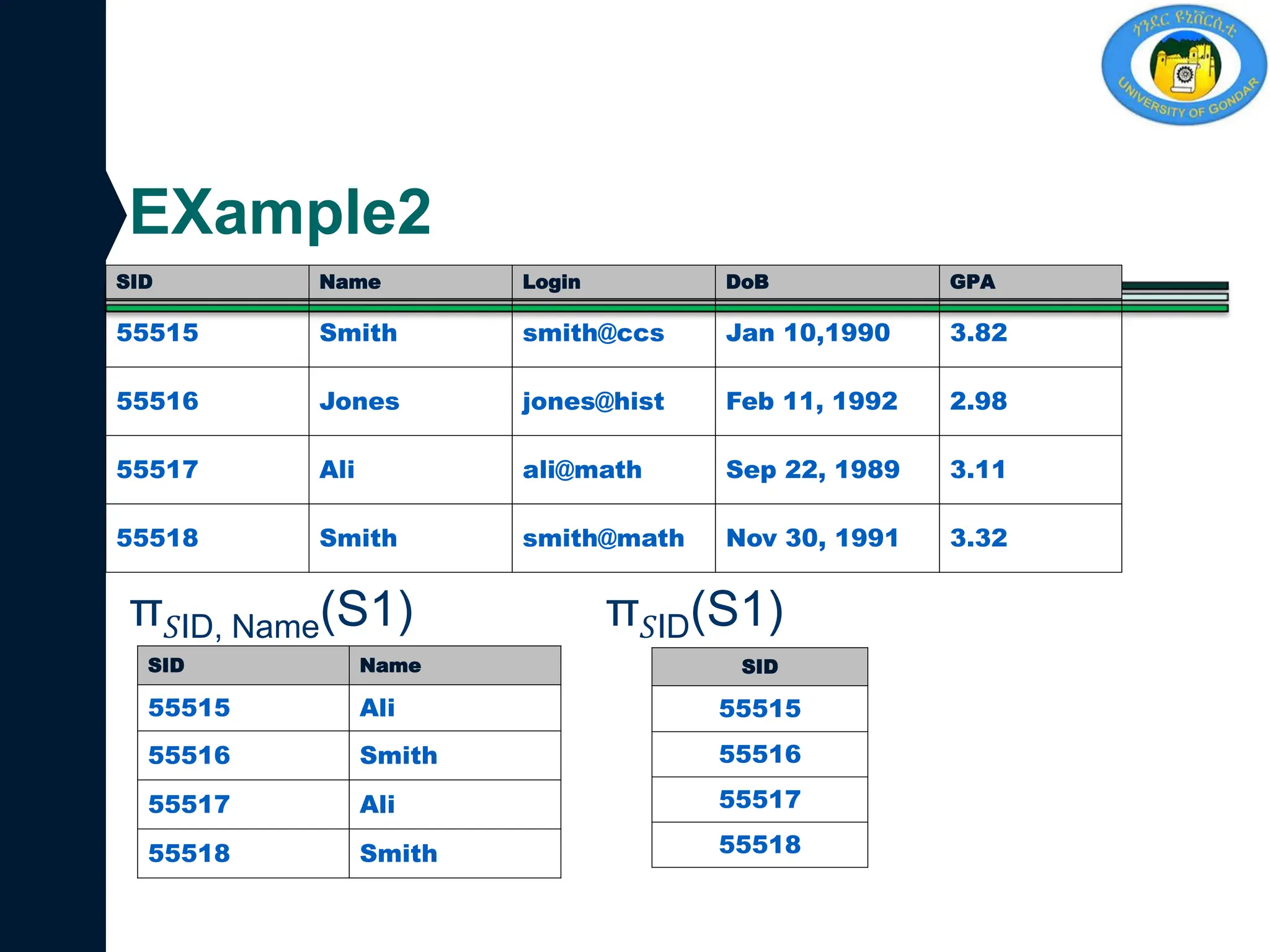
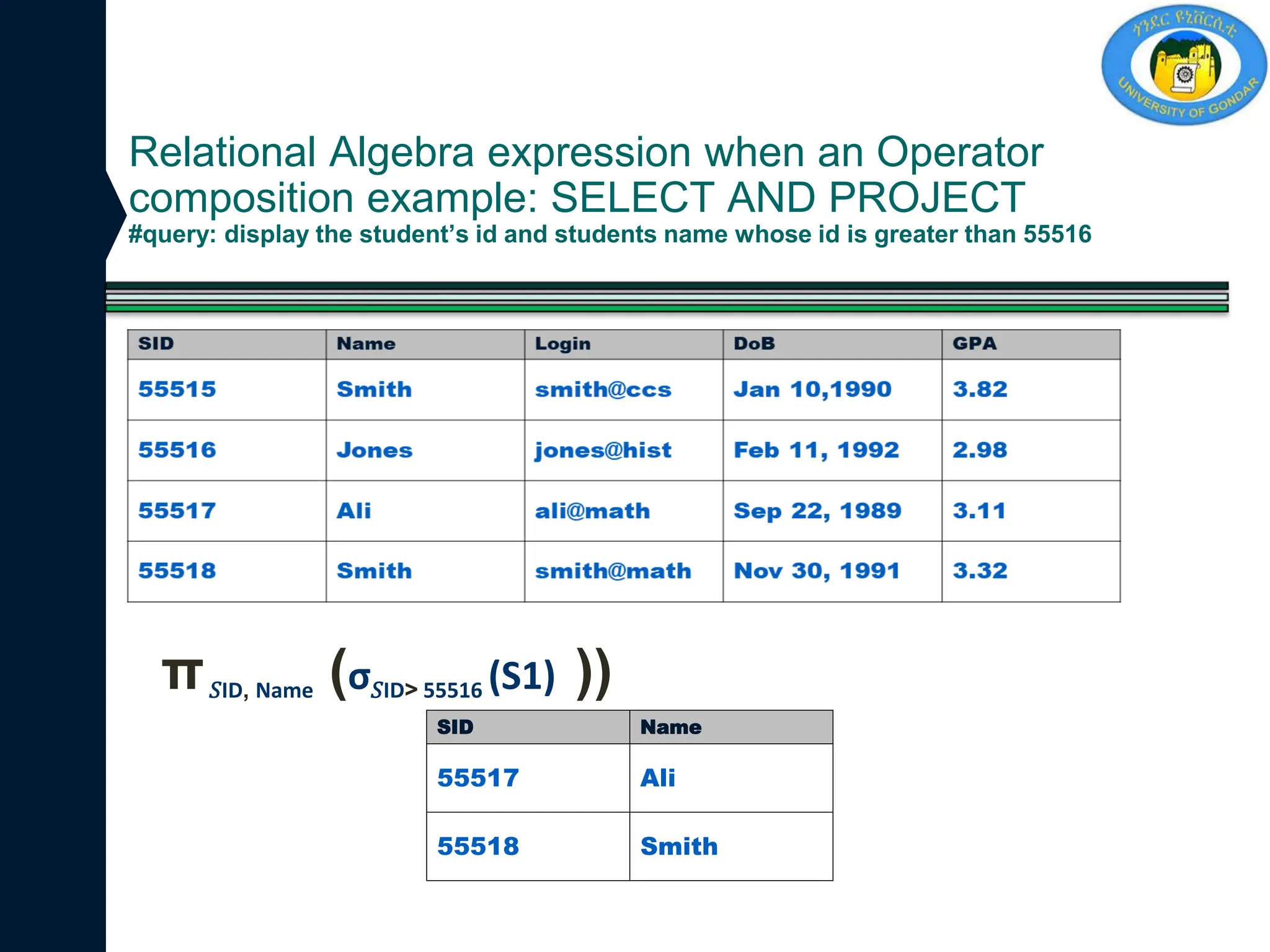
 Table-1: Customer Table-2: Loan
Customer name Street City
Debomit Kadamtala Alipurduar
Sayantan Udaypur Balurghat
Soumya Nutanchati Bankura
Ritu Juhu Mumbai
Loan
number
Branch
name
Amount
L01 Main 200
L03 Main 150
L10 Sub 90
L08 Main 60

 Consider the following student table
 Display the Last-name of student
where age is greater than 30
Soln:{t.Lname|student(t) and t.age>30}
output:
 Display all the details of student
where name is ‘neba’
Soln:{t|student(t) and t.Lname=‘neba’}
Fname Lname age
samson ayu 30
abie neba 28
masho neba 27
fedel tamiru 31
dawit miki 32
Lname
tamiru
miki
Fname Lname age
abie neba 28
masho neba 27

2. Domain Relational Calculus (DRC)
 In domain relational calculus, filtering variable uses the domain of
attributes. Domain relational calculus uses the same operators as tuple
calculus. It uses logical connectives ∧ (and), ∨ (or) and ┓ (not). It uses
Existential (∃) and Universal Quantifiers (∀) to bind the variable. The
Query by example is a query language related to domain relational calculus.
 Notation:
– { a1, a2, a3, ..., an | P (a1, a2, a3, ... ,an)}
– Where
– a1,a2 are attributes
P stands for formula built by inner attributes
 For example:
– {< article, page, subject > | ∈ javatpoint ∧ subject = 'database'}
– Output: This query will yield the article, page, and subject from the
relational javatpoint, where the subject is a database.

 Consider the following student table
 Find the Last-name and age of student
where age is greater than 30
Soln:{ <Lname, age>| ∈ student and
age>30 }
output:
Fname Lname age
samson ayu 30
abie neba 28
masho neba 27
fedel tamiru 31
dawit miki 32
Lname age
tamiru 31
miki 32

chapter 6 Relational Algebra and calculus.pdf

More Related Content

Similar to chapter 6 Relational Algebra and calculus.pdf

More from Getnet Tigabie Askale -(GM)

Recently uploaded

chapter 6 Relational Algebra and calculus.pdf