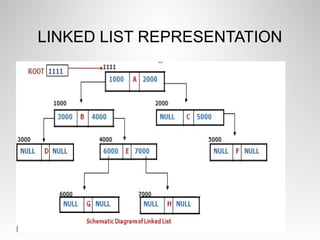
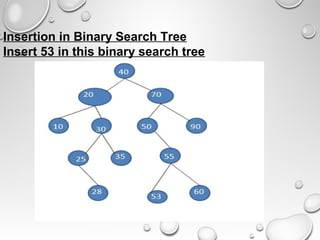
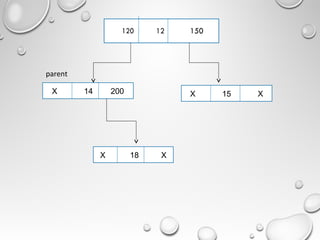
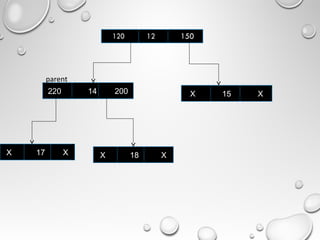
The document outlines a presentation on trees and binary trees. It discusses different tree types including binary trees, complete binary trees, and binary search trees. It covers tree traversal methods like preorder, inorder and postorder traversal. It also discusses representations of binary trees using arrays and linked lists and algorithms for insertion and deletion in binary search trees.

1. PRESENTED BY:
TABISH HAMID
PRIYANKA MEHTA
CONTACT NO: 08376023134
Submitted to:
MISS. RAJ BALA SIMON

2. TREES
SESSION OUTLINE:
• TREE
• BINARY TREE
• TREES TRAVERSAL
• BINARY SEARCH TREE
• INSERTION AND DELETION IN BINARY SEARCH TREE
• AVL TREE

3. TREES
• TREE DATA STRUCTURE IS MAINLY USED
TO REPRESENT DATA CONTAINING A
HIERARCHICAL RELATIONSHIP BETWEEN
ELEMENTS .

4. TREES
• COLLECTION OF NODESOR
FINITE SET OF NODES
• THIS COLLECTION CAN BE EMPTY.
• DEGREE OF A NODE IS NUMBER OF NODES
CONNECTED TO A PARTICULAR NODE.

5. TREES LEVELS

6. • A PATH FROM NODE N1 TO NK IS
DEFINED AS A SEQUENCE OF
NODES N1, N2, …….., NK.
• THE LENGTH OF THIS PATH IS THE
NUMBER OF EDGES ON THE PATH.
• THERE IS A PATH OF LENGTH ZERO
FROM EVERY NODE TO ITSELF.
• THERE IS EXACTLY ONE PATH
FROM THE ROOT TO EACH NODE IN
A TREE.
TREES

7. • HEIGHTOF A NODE IS THE LENGTH OF A
LONGEST PATH FROM THIS NODE TO A LEAF
• ALL LEAVES ARE AT HEIGHT ZERO
• HEIGHT OF A TREE IS THE HEIGHT OF ITS ROOT
(MAXIMUM LEVEL)
TREES

8. • DEPTHOF A NODE IS THE LENGTH OF PATH
FROM ROOT TO THIS NODE
• ROOT IS AT DEPTH ZERO
• DEPTH OF A TREE IS THE DEPTH OF ITS
DEEPEST LEAF THAT IS EQUAL TO THE
HEIGHT OF THIS TREE
TREES

9. BINARY TREE
Complete binary treeFull binary tree

10. FULL BINARY TREE
A binary tree is said to
be full if all its leaves
are at the same level
and every internal node
has two
children.
The full binary tree of
height h has
l = 2h
leaves
and
m = 2h
– 1 internal
nodes.

11. COMPLETE BINARY TREE
A complete binary tree is
either a full binary tree or one
that is full except for a
segment of missing leaves
on the right side of the
bottom level.

12. PICTURE OF A BINARY TREE
a
b c
d e
g h i
l
f
j k

13. TREE TRAVERSALS
• PRE-ORDER
• N L R
• IN-ORDER
• L N R
• POST-ORDER
• L R N

14. TREE TRAVERSALS
PRE-ORDER(NLR)
1, 3, 5, 9, 6, 8

15. TREE TRAVERSALS
IN-ORDER(LNR)
5, 3, 9, 1, 8, 6

16. TREE TRAVERSALS
POST-ORDER(LRN)
5, 9, 3, 8, 6, 1

17. TREE TRAVERSALS
IN-ORDER TRAVERSAL : 1,2,3,4,5,6,7,8,9
PREORDER TRAVERSAL:1,2,4,7,5,8,3,6,9
ARE GIVEN.
DRAW BINARY TREE FROM THESE TWO
TRAVERSALS?

18. In:4,7,2,8,5
Pre:2,4,7,5,8
In:6,9,3
Pre:3,6,9
1

19. 7
6
1
2
5
4
8
3
9

20. REPRESENTATION OF BINARY TREE
i)SEQUENTIAL REPRESENTATION (ARRAYS)
ii)LINKED LIST REPRESENTATION

21. I) SEQUENTIAL REPRESENTATION
(ARRAYS)
REQUIRED THREE DIFFERENT ARRAYS
1.ARR (CONTAIN ITEMS OF TREE)
2.LC (REPRESENT LEFT CHILD)
3.RC (REPRESENT RIGHT CHILD)

22. SEQUENTIAL REPRESENTATION
(ARRAYS)
A B C D E ‘0’ F
1 3 -1 -1 -1 -1 -1
2 4 6 -1 -1 -1 -1
arr
lc
rc

23. LINKED LIST REPRESENTATION

24. IN LINKED LIST REPRESENTATION
EACH NODE HAS THREE FIELDS:-
DATA PART
ADDRESS OF THE LEFT SUBTREE.
ADDRESS OF THE RIGHT SUBTREE

25. EXTENDED BINARY TREE
A BINARY TREE CAN BE CONVERTED TO AN EXTENDED BINARY
TREE BY ADDING NEW NODES TO ITS LEAF NODES AND TO
THE NODES THAT HAVE ONLY ONE CHILD. THESE NEW NODES
ARE ADDED IN SUCH A WAY THAT ALL THE NODES IN
RESULTANT TREE HAVE ZERO OR TWO CHILDREN.
IT IS ALSO KNOWN AS 2-TREE.THE NODES OF THE ORIGINAL
TREE ARE CALLED INTERNAL NODES.
NEW NODES THAT ARE ADDED TO BINARY TREE ,TO MAKE IT
AN EXTENDED BINARY TREE ARE CALLED EXTERNAL NODES.
25

26. .
Binary Tree Extended Binary Tree

27. Binary Search tree
It is a tree that may be empty.
and non-empty binary Search tree satisfies the
following properties :-
(1)Every element has a key or value and no two
elements have the same key that is all keys are
unique.
(2) The keys if any in the left sub tree of the root
are smaller than the key in the node.
(3) The keys if any in the right sub tree of the root
are larger than the key in the node.
(4) Left and Right sub trees of the root are also
binary search tree.

28. Example of the Binary Search Tree :-
The input list is
20 17 6 8 10 7 18 13 12 5
20
17
6 18
5
8
7 10
13
12

29. Insertion in Binary Search Tree
Insert 53 in this binary search tree

30. Representation of Binary Search Tree :-
struct btreenode
{
struct btreenode *left;
int data;
struct btreenode *right;
};

31. Function code of Inorder :-
void inorder(struct btreenode *sr)
{
if(sr!=NULL)
{
inorder(sr->left);
printf(“%d”,sr->data);
inorder(sr->right);
}
}

32. Function code of Preorder :-
void preorder(struct btreenode *sr)
{
if(sr!=NULL)
{
printf(“%d”,sr->data);
preorder(sr->left);
preorder(sr->right);
}
}

33. Function code of Postorder :-
void postorder(struct btreenode *sr)
{
if(sr!=NULL)
{
postorder(sr->left);
postorder(sr->right);
printf(“%d”,sr->data);
}
}

34. Function code for Insertion of a node in
binary search tree-
void insert(struct btreenode **sr,int num)
{
if(*sr==NULL)
{
*sr=malloc (sizeof(struct btreenode))
(*sr)->left=NULL;
(*sr)->data=num;
(*sr)->right=NULL;
}

35. else
{
if(num<(sr)->data)
insert(&((*sr)->left),num);
else
insert(&((*sr)->right),num);
}
}

36. CASES FOR DELETION
• IF NODE HAS NO SPECIFIC DATA OR NO CHILD
• IF NODE HAS ONLY LEFT CHILD.
• IF NODE HAS ONLY RIGHT CHILD
• IF NODE HAS TWO CHILDREN

37. CASE 1
• IF NODE TO BE DELETED HAS NO CHILD
IF (( X->LEFT == NULL) && (X->RIGHT == NULL))
{
• IF ( PARENT ->RIGHT == X)
• PARENT -> RIGHT = NULL;
• ELSE
• PARENT -> LEFT = NULL;
• FREE (X);
}

39. X 14 200 X 15 X
X 18 X
parent

40. CASE 2
IF NODE TO BE DELETED HAS ONLY RIGHT CHILD
IF (( X-> LEFT==NULL) && (X-> RIGHT !=NULL))
{
• IF (PARENT -> LEFT == X)
• PARENT ->LEFT = X-> RIGHT;
• ELSE
• PARENT ->RIGHT = X-> RIGHT;
• FREE (X);
}

41. 180 14 200 X 15 X
X 16 220 X 18 X
X 17 X
parent
X

42. 220 14 200 X 15 X
X 18 XX 17 X
parent

43. CASE 3
IF NODE HAS ONLY LEFT CHILD
IF((X->LEFT!=NULL)&&(X->RIGHT==NULL))
{
IF (PARENT->LEFT==X)
PARENT->LEFT=X->LEFT;
ELSE
PARENT->RIGHT->X->LEFT;
FREE(X);
}

44. 180 14 200 X 15 X
X 16 X
220 18 X
X 17 X
parent
X

45. 180 14 220 X 15 X
X 16 220
X 17 X
parent

46. CASE 4
IF NODE TO BE DELETED HAS TWO CHILDREN
IF((X-> LEFT !=NULL) && (X-> RIGHT!=NULL))
{ PARENT = X;
XSUCC= X->RIGHT;
WHILE (XSUCC->LEFT!=NULL)
{
PARENT = XSUCC;
XSUCC =XSUCC-> LEFT;
}
X->DATA = XSUCC->DATA;
X=XSUCC }

47. X 15 X 180 14 200
X 16 X
240 18 220
X 17 X X 19 X
parent
X
XSUCC

48. X 15 X 180 17 200
X 16 X
X 18 220
X 19 X