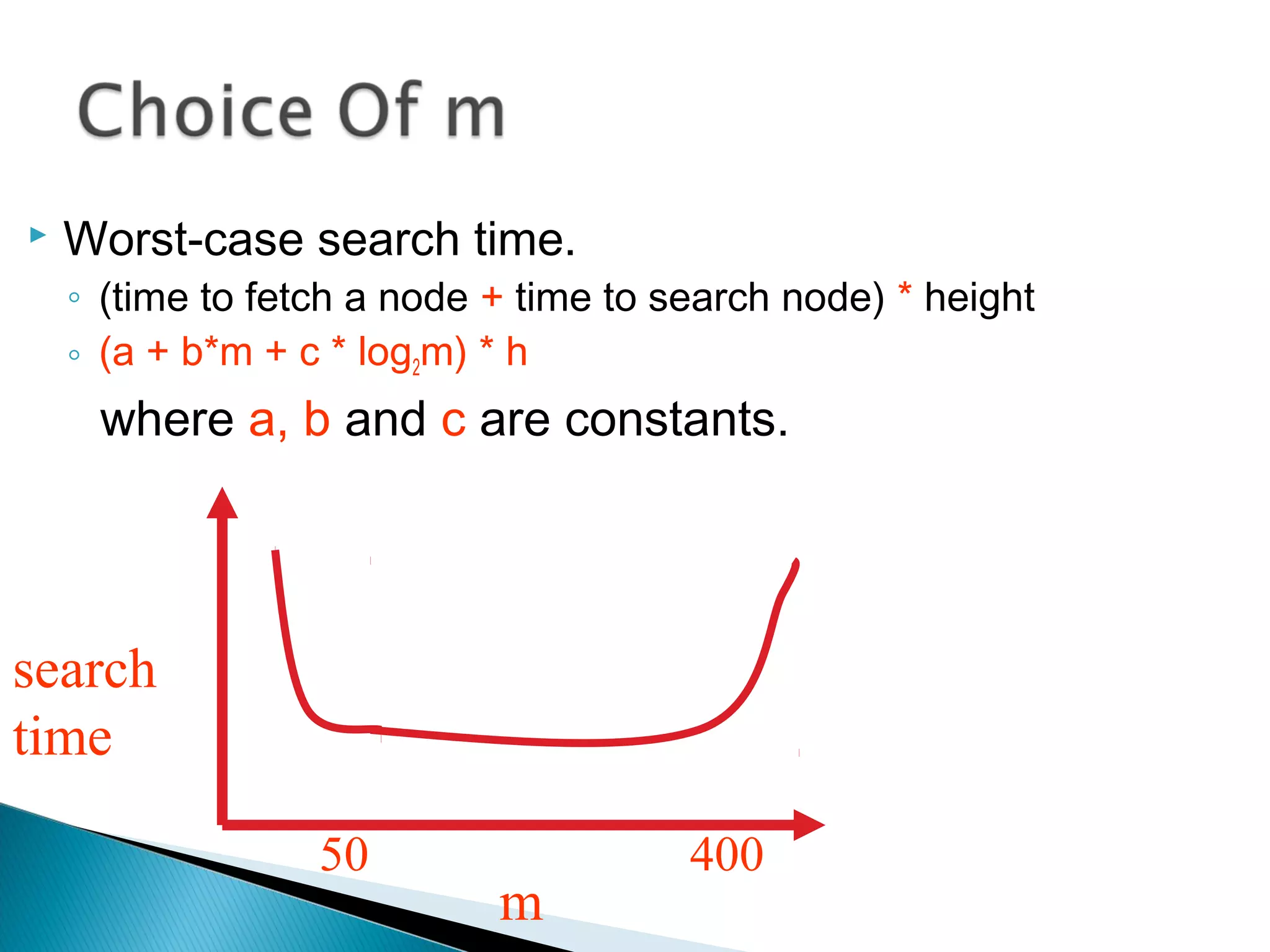
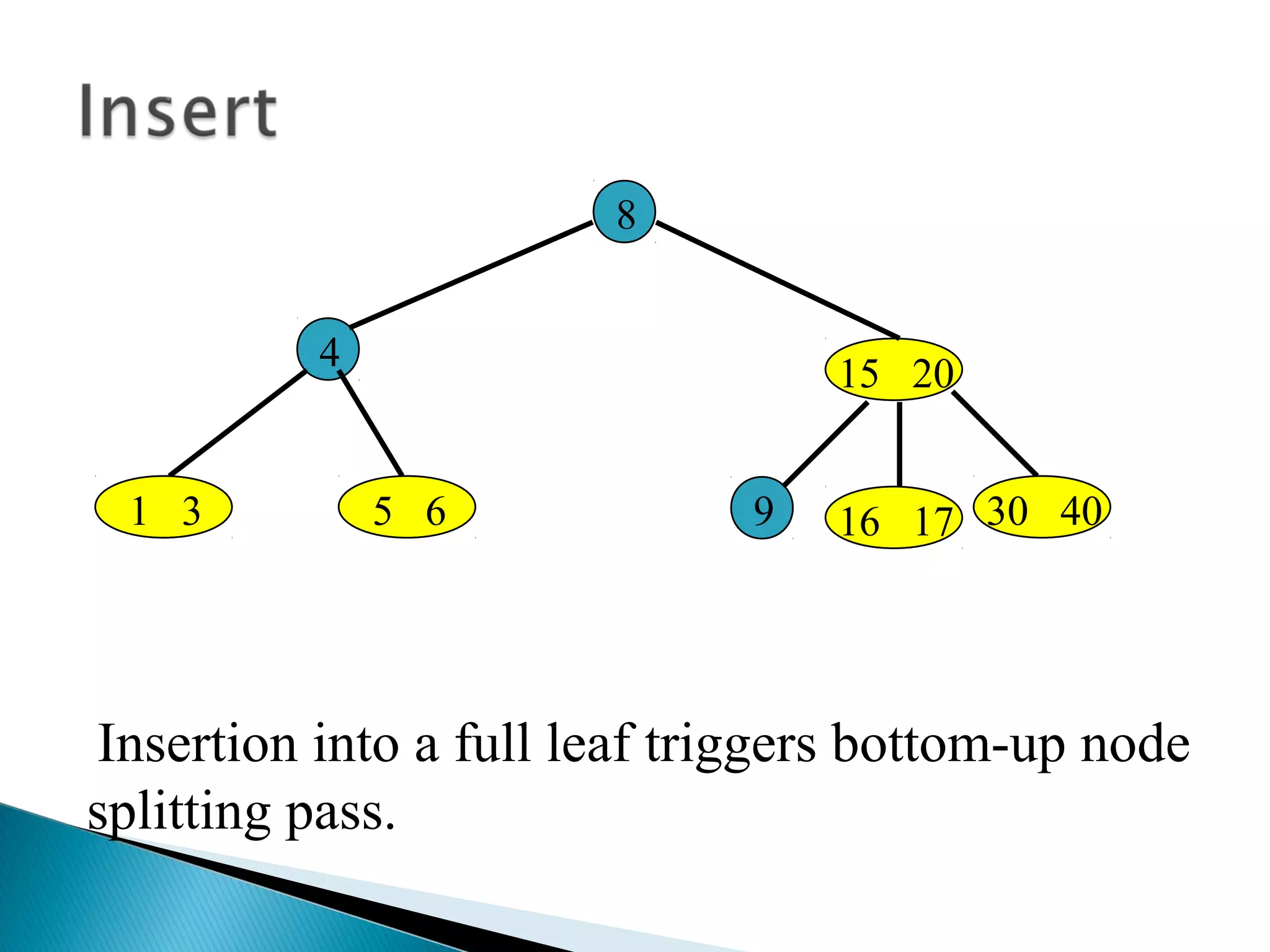
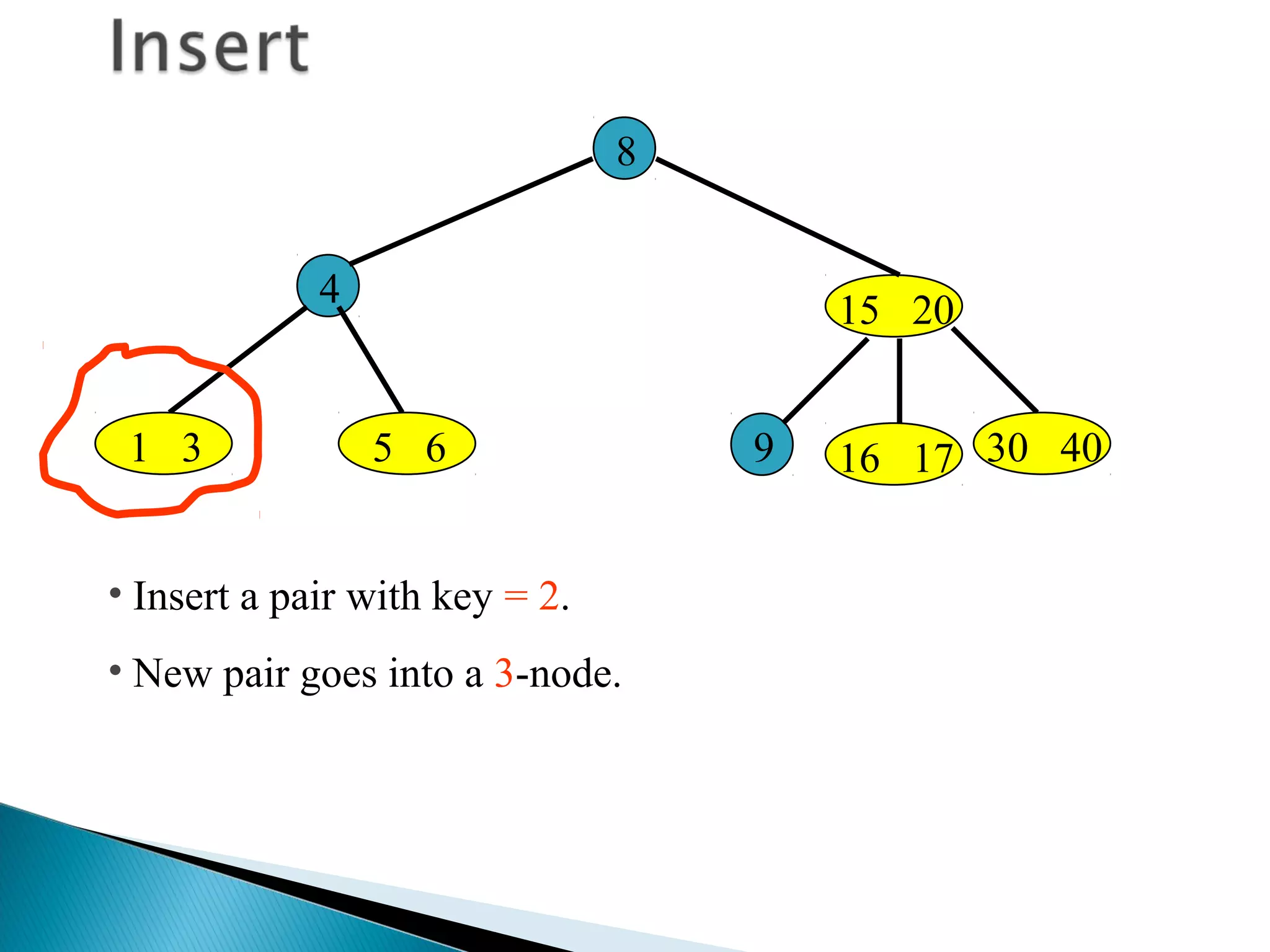
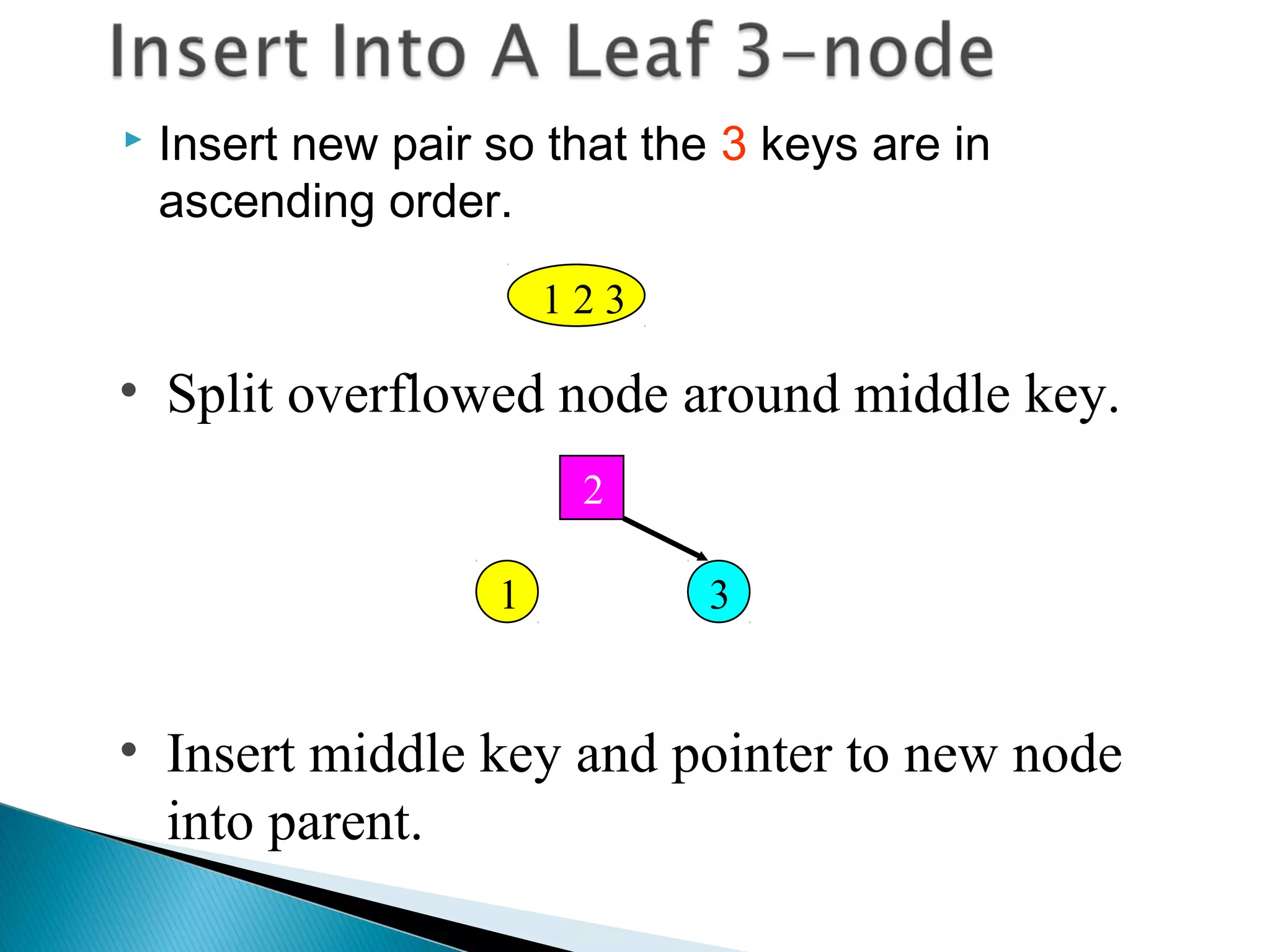
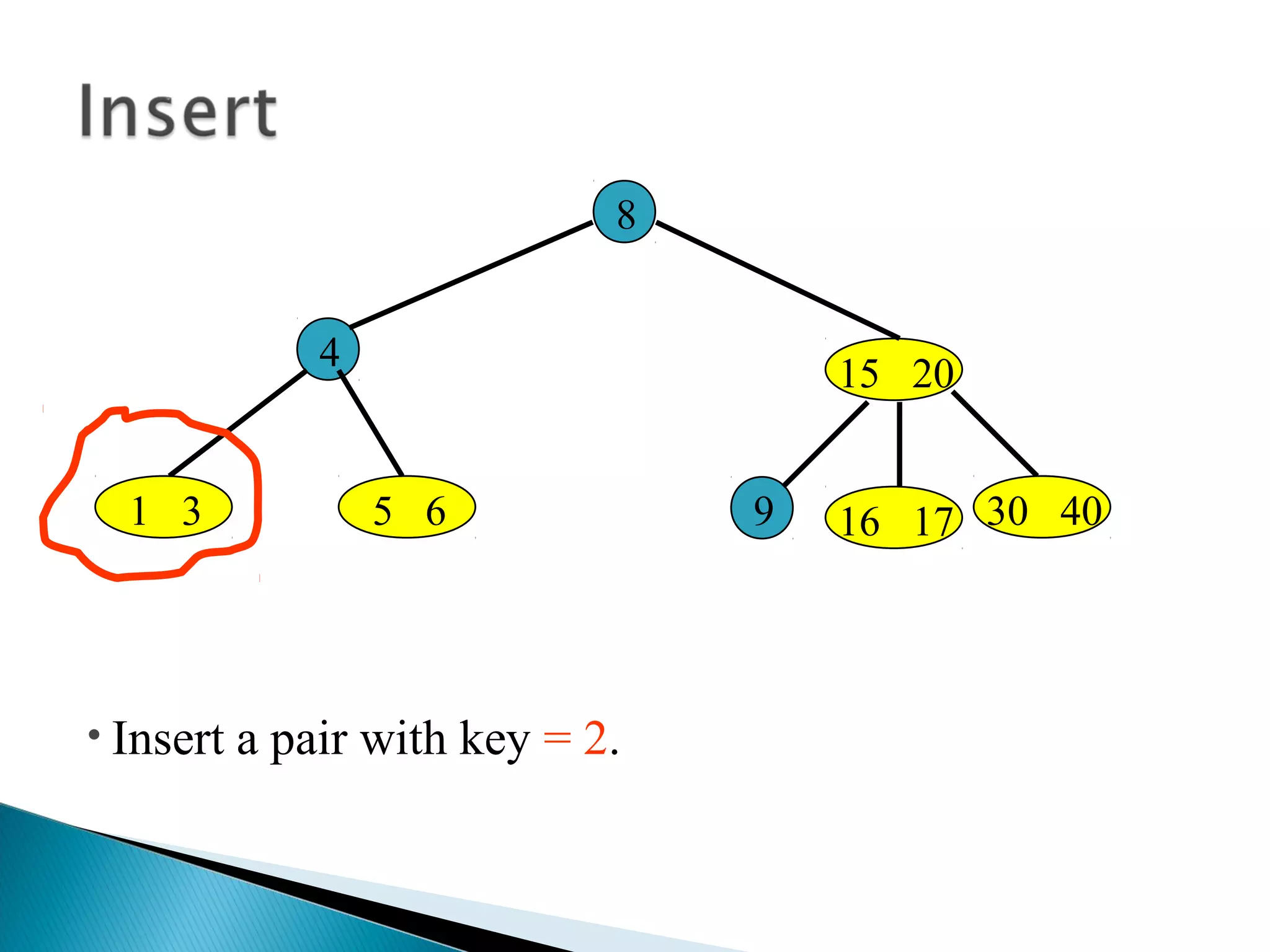
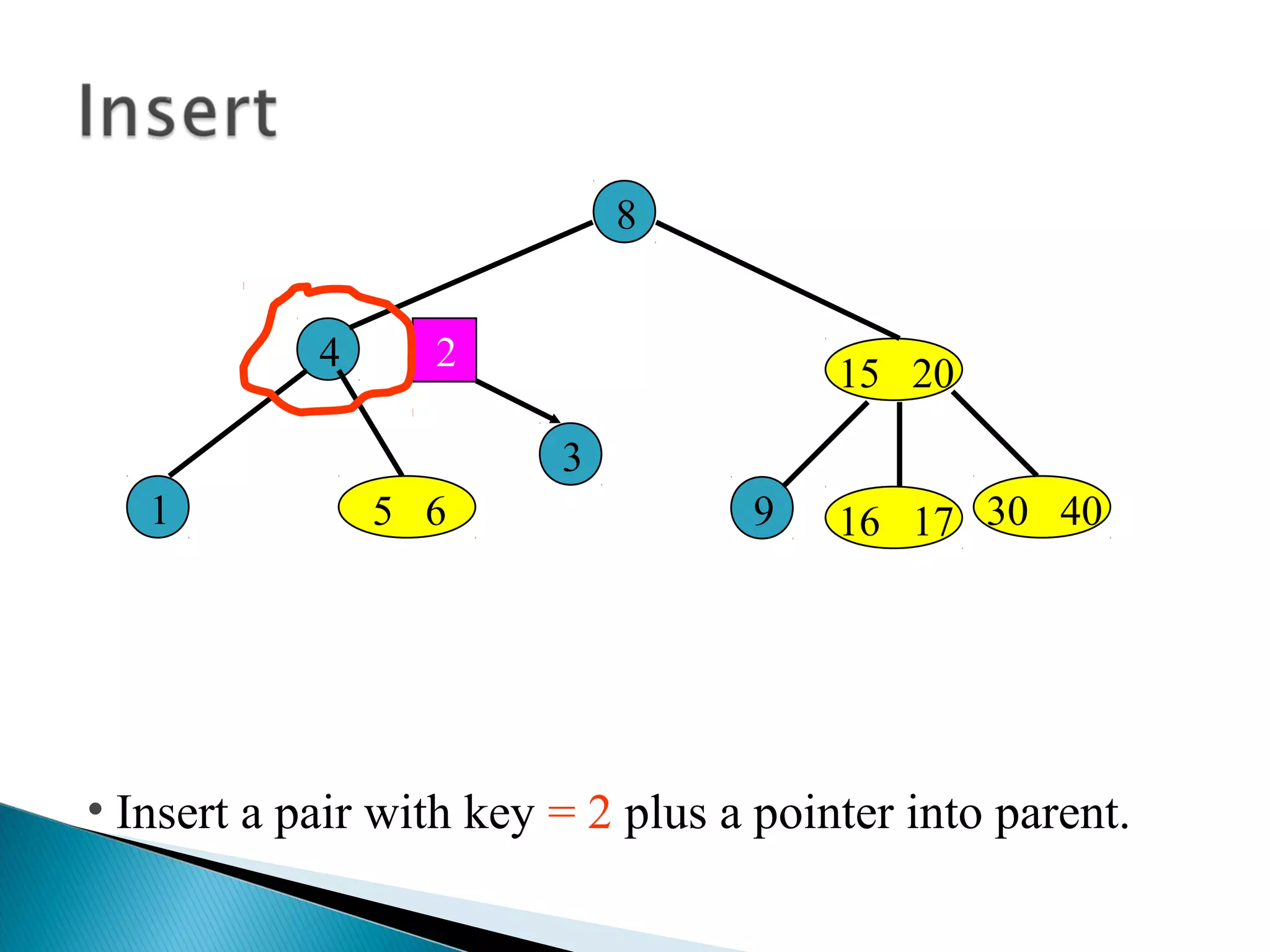
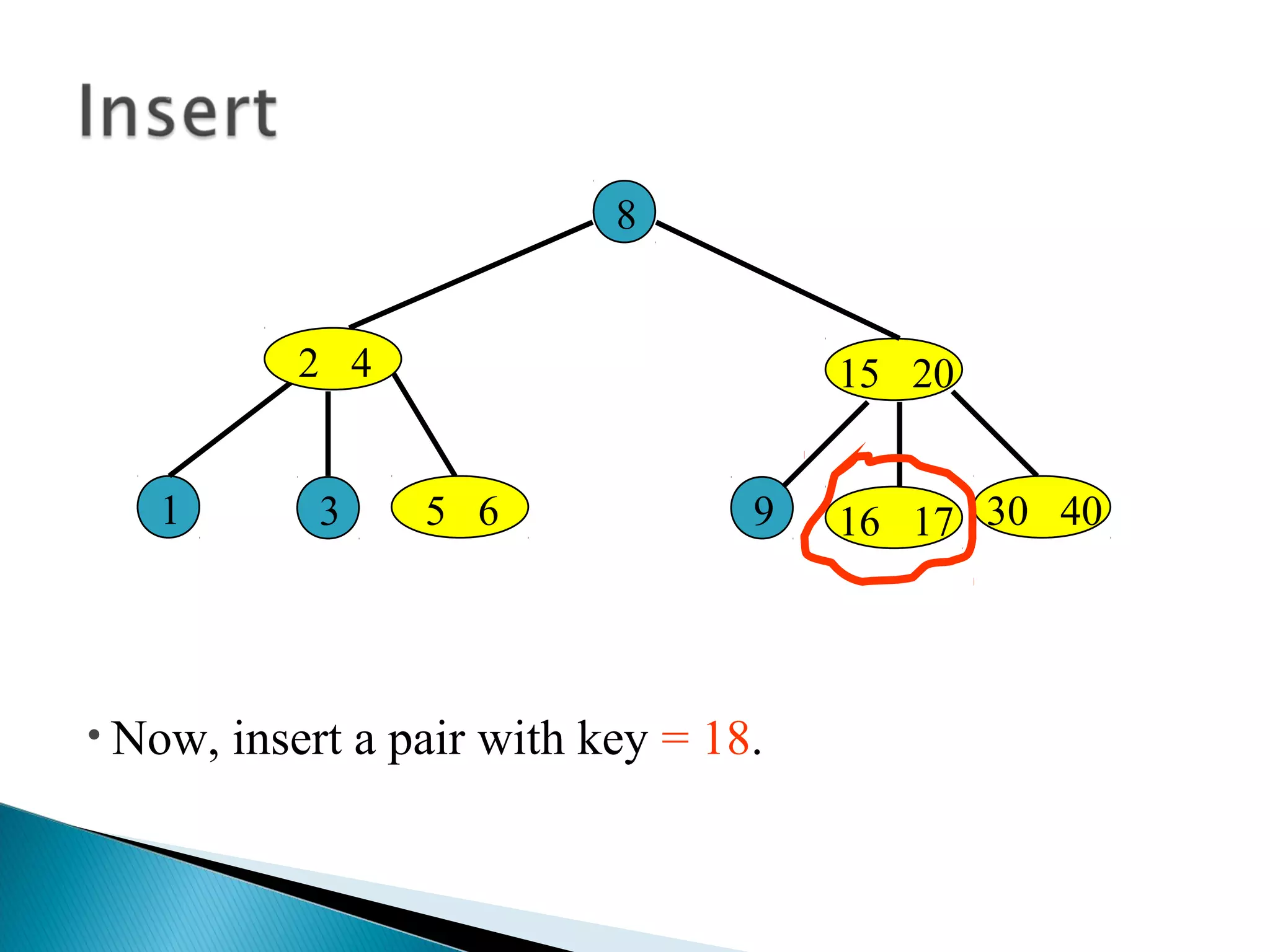
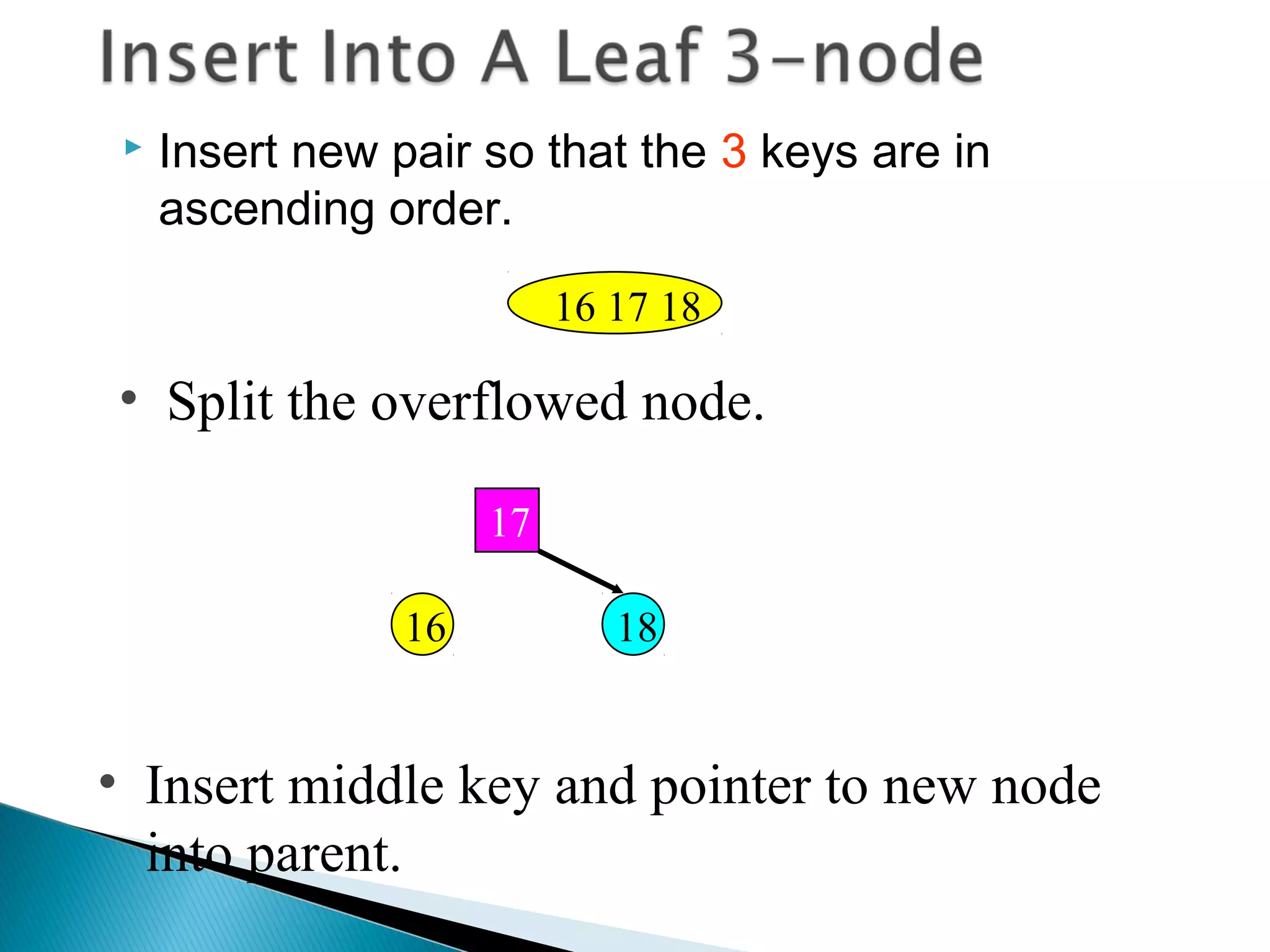
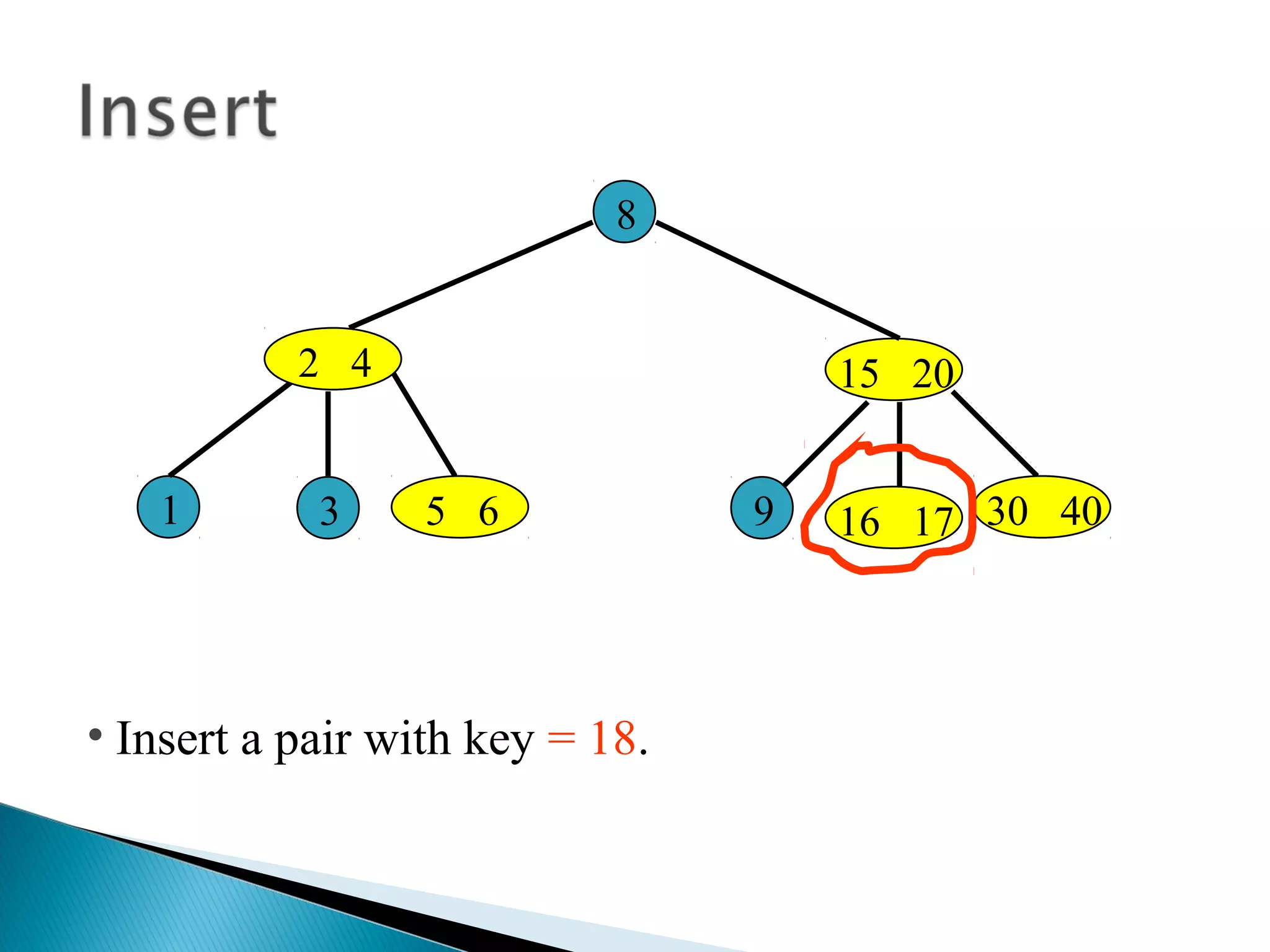
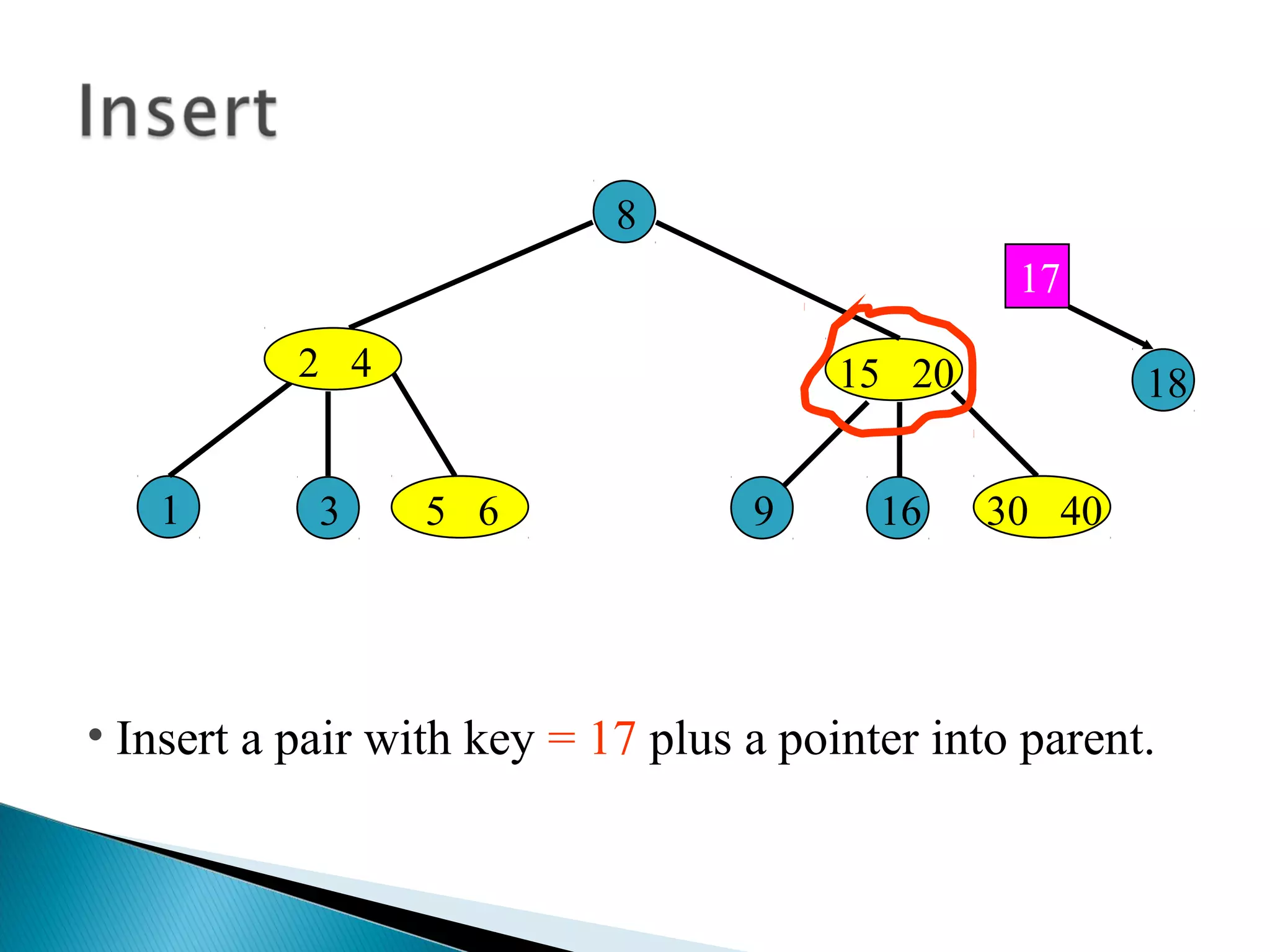
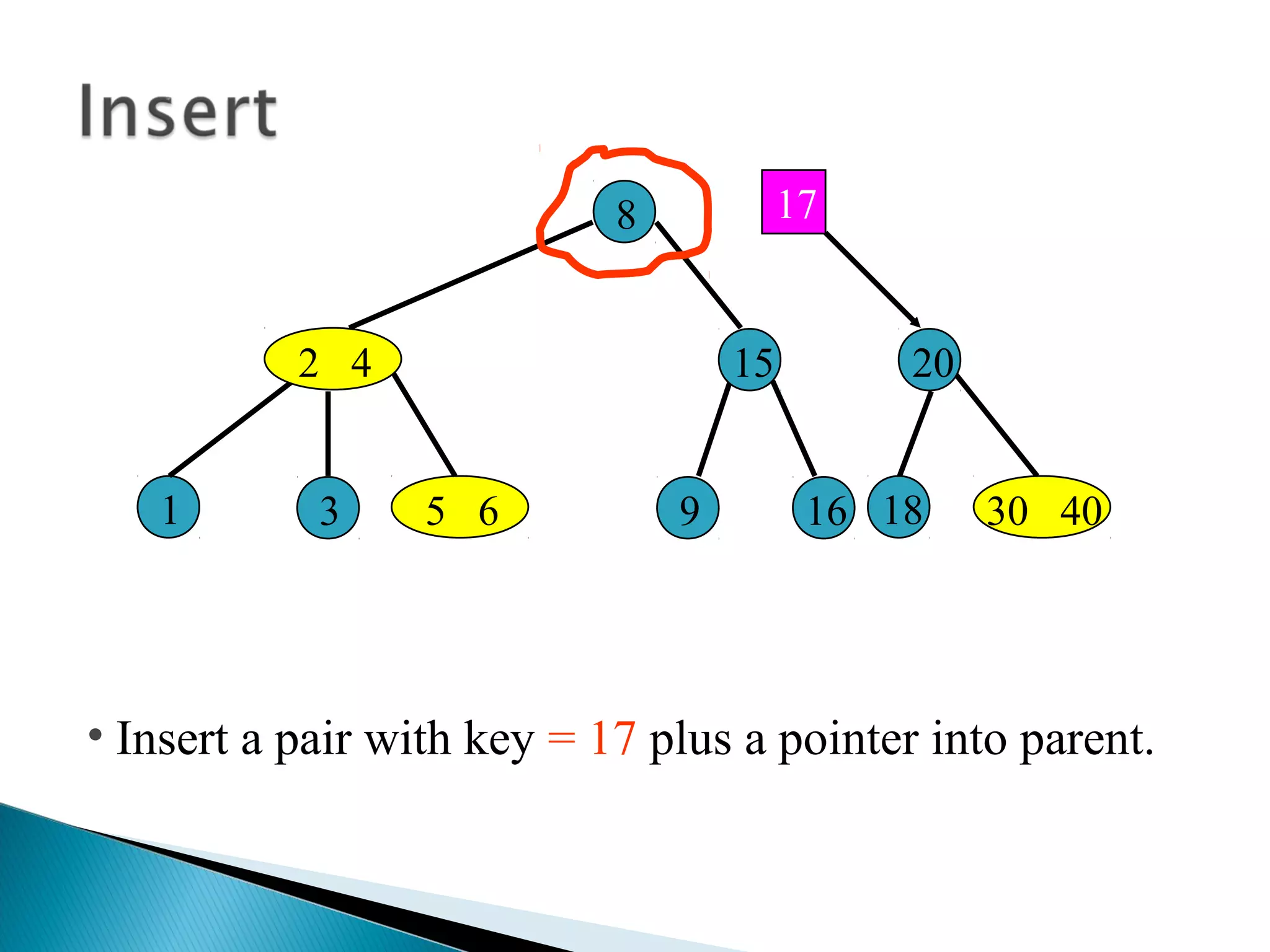
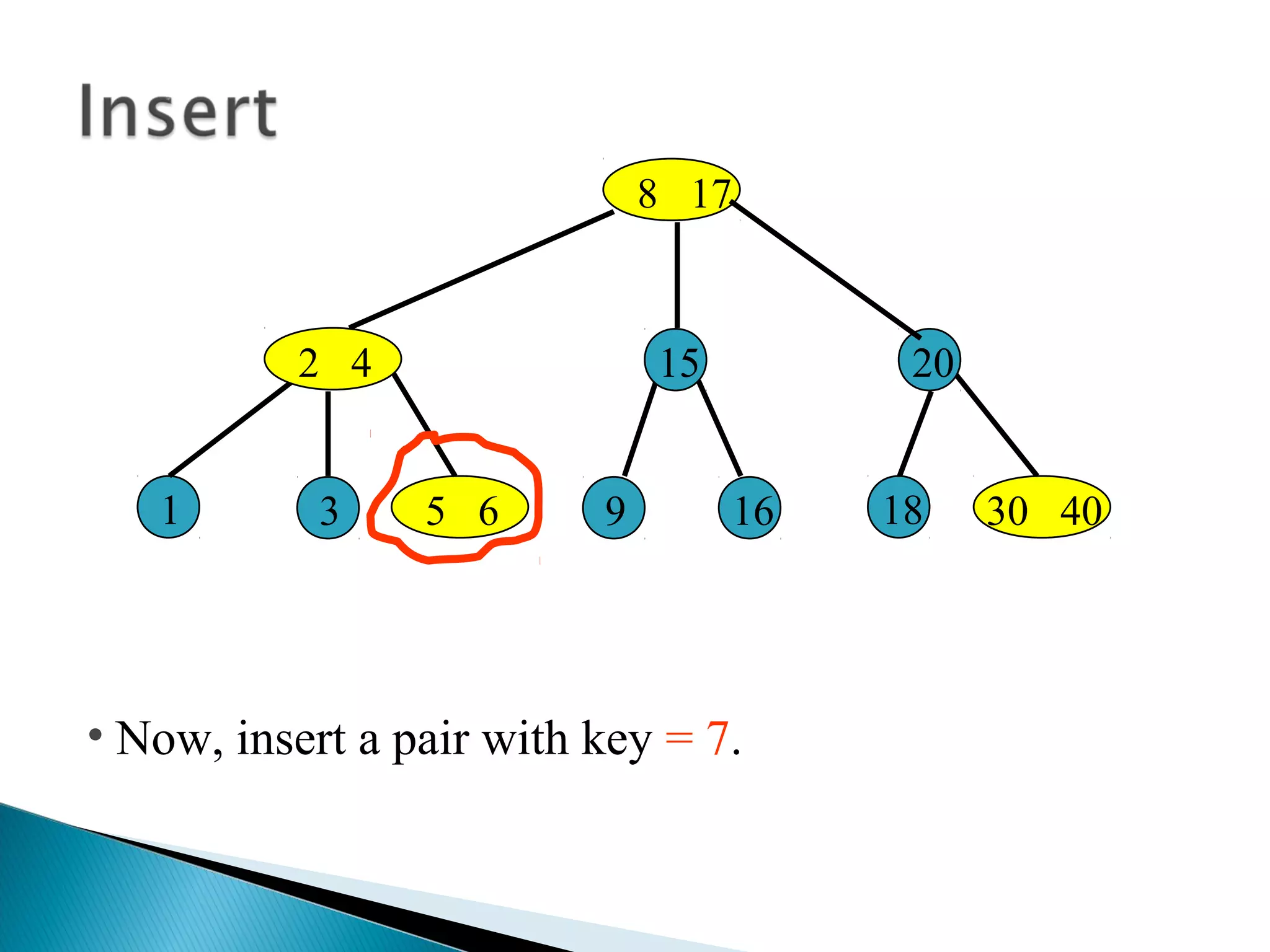
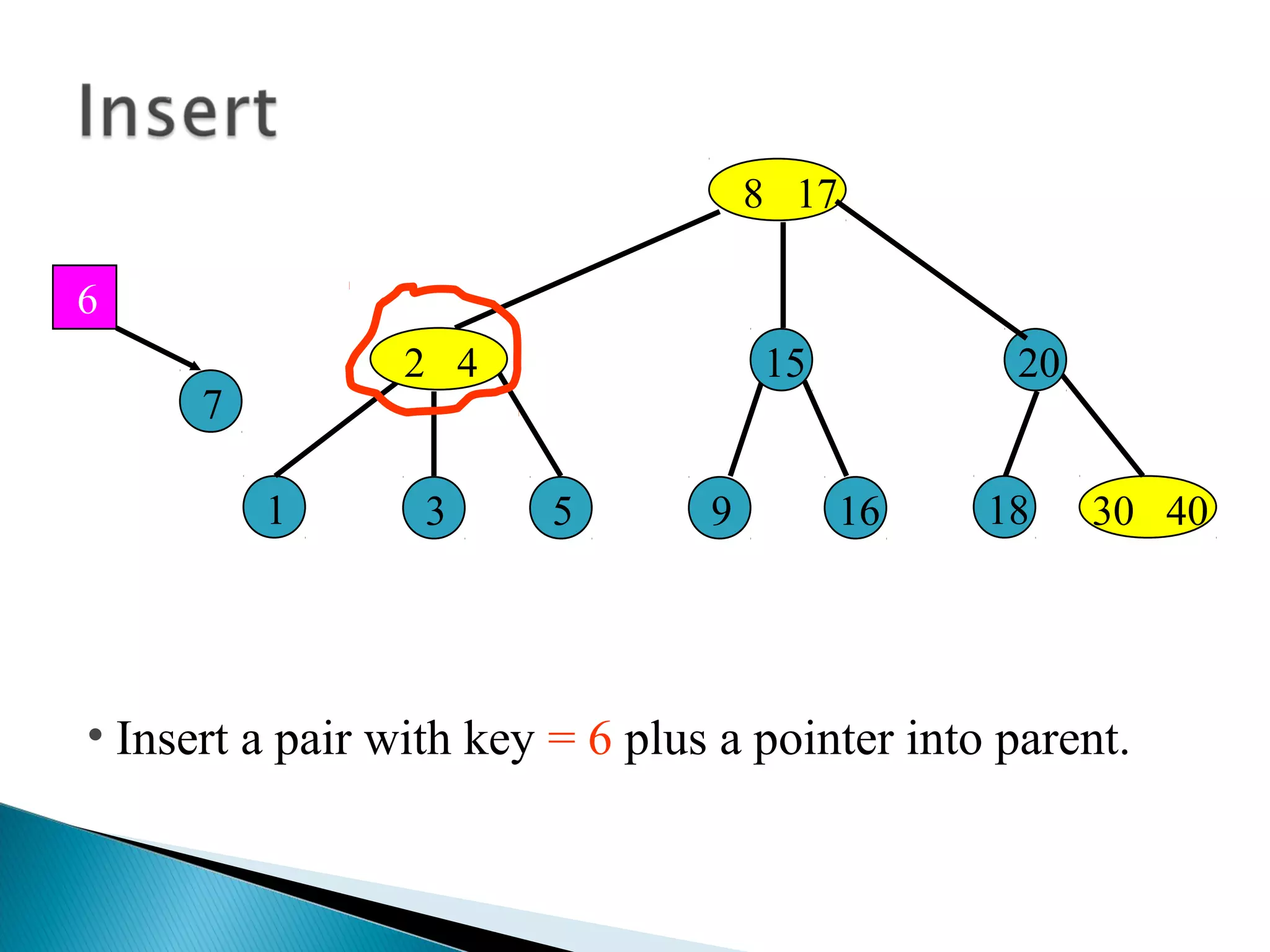
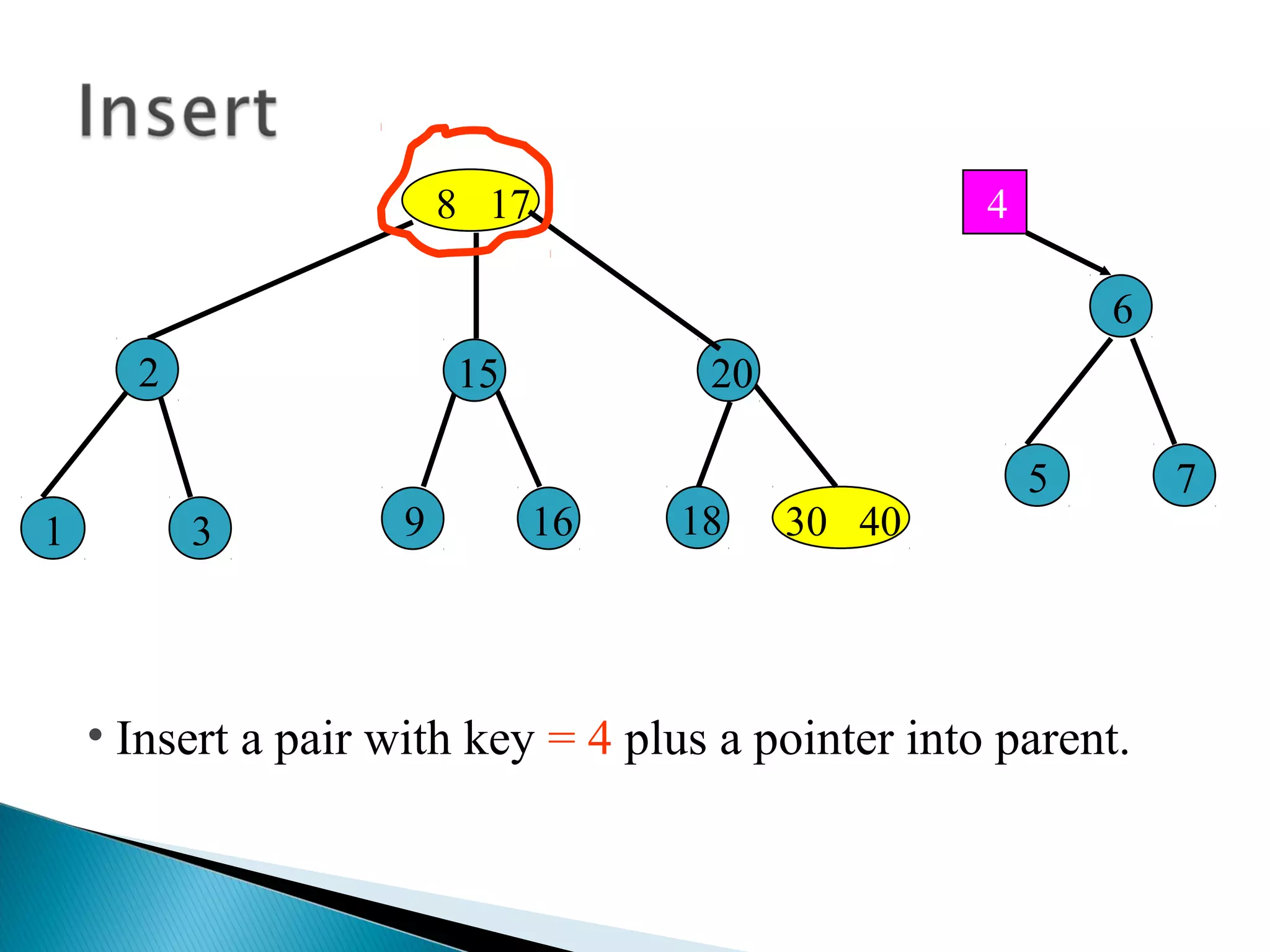
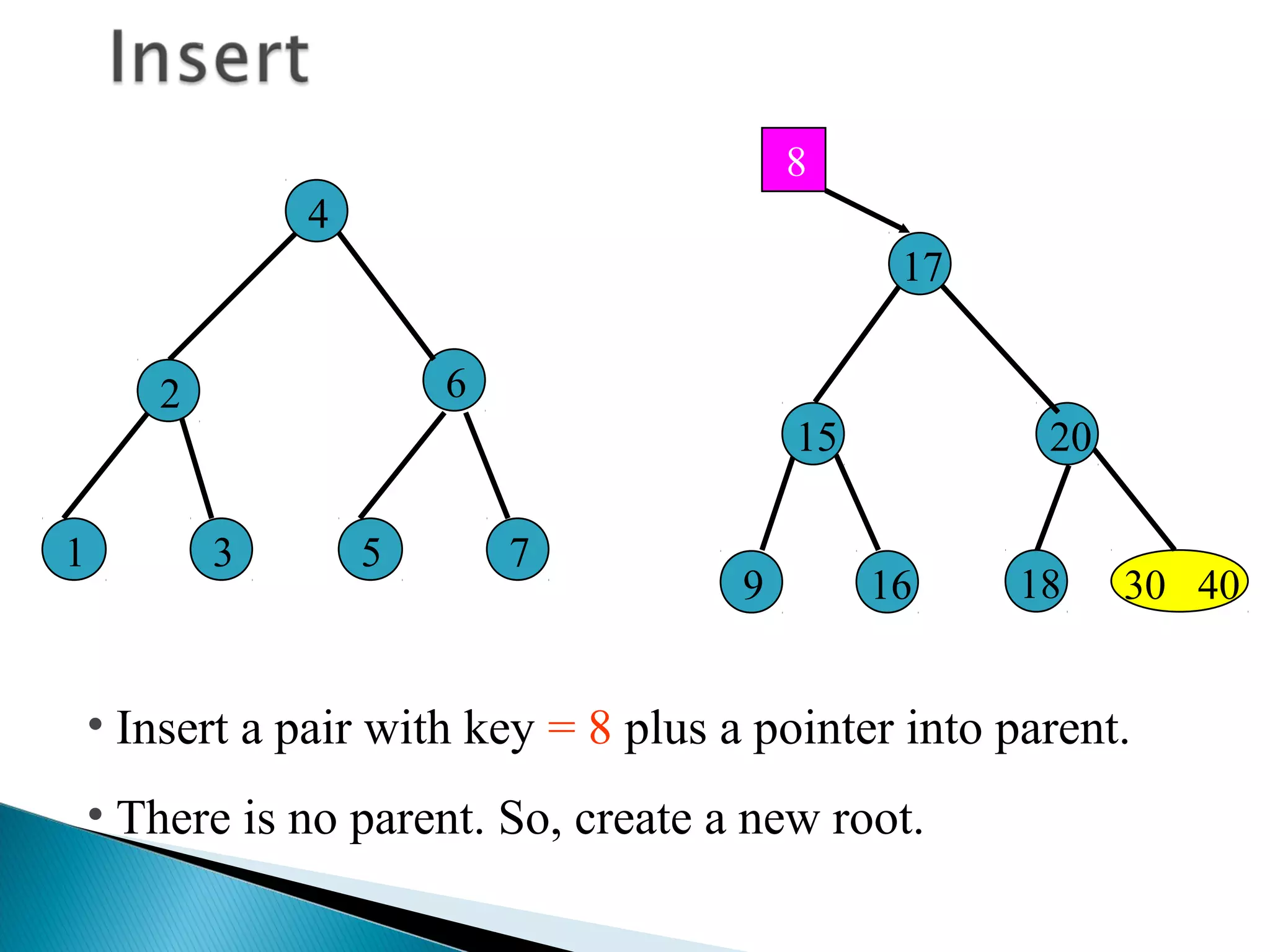
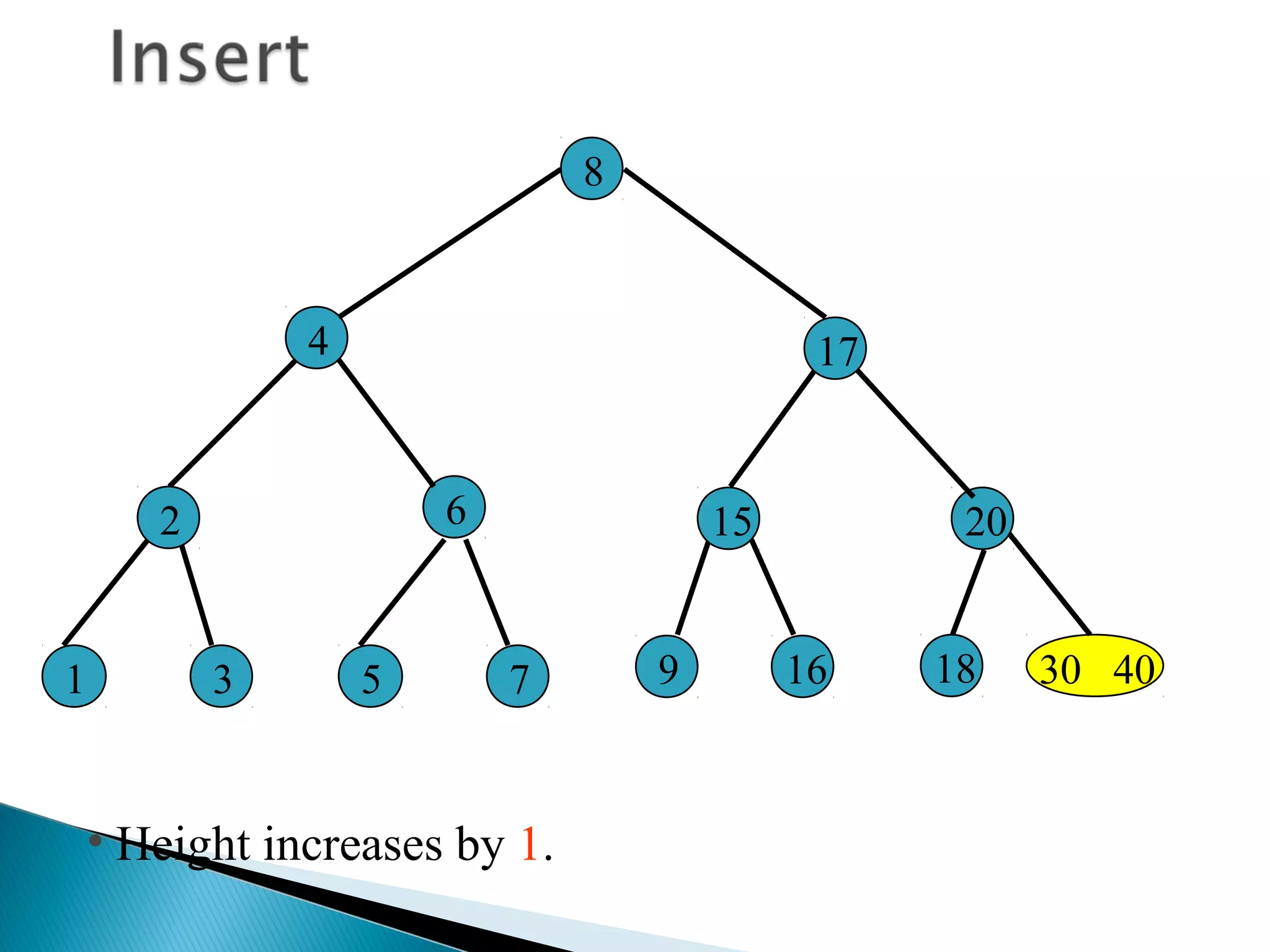
The document discusses B-trees, which are self-balancing search trees used to store large datasets. B-trees overcome limitations of storing data in memory by keeping the tree partially balanced and stored on disk. The document outlines properties of B-trees including that internal nodes must have a minimum number of children based on the tree's order, and that inserting data may cause nodes to split and keys to propagate up the tree to maintain balance.

1.  Large degree B-trees used to represent very large
dictionaries that reside on disk.
 Smaller degree B-trees used for internal-memory
dictionaries to overcome cache-miss penalties.

2.  Definition assumes external nodes (extended
m-way search tree).
 B-tree of order m.
◦ m-way search tree.
◦ Not empty => root has at least 2 children.
◦ Remaining internal nodes (if any) have at least
ceil(m/2) children.
◦ External (or failure) nodes on same level.

3.  B-tree of order m.
◦ m-way search tree.
◦ Not empty => root has at least 2 children.
◦ Remaining internal nodes (if any) have at least
ceil(m/2) children.
◦ External (or failure) nodes on same level.
• 2-3 tree is B-tree of order 3.
• 2-3-4 tree is B-tree of order 4.

4.  B-tree of order m.
◦ m-way search tree.
◦ Not empty => root has at least 2 children.
◦ Remaining internal nodes (if any) have at least
ceil(m/2) children.
◦ External (or failure) nodes on same level.
• B-tree of order 5 is 3-4-5 tree (root may be
2-node though).
• B-tree of order 2 is full binary tree.

5.  n = # of pairs.
 # of external nodes = n + 1.
 Height = h => external nodes on level h + 1.
1 1
2 >= 2
3 >= 2*ceil(m/2)
h + 1 >= 2*ceil(m/2)h-1
n + 1 >= 2*ceil(m/2)h-1
, h >= 1
level # of nodes

6.  m = 200.
n + 1 >= 2*ceil(m/2)h-1
, h >= 1
height # of pairs
2 >= 199
3 >= 19,999
4 >= 2 * 106
–1
5 >= 2 * 108
–1
h <= log ceil(m/2) [(n+1)/2] + 1

7.  Worst-case search time.
◦ (time to fetch a node + time to search node) * height
◦ (a + b*m + c * log2m) * h
where a, b and c are constants.
m
search
time
50 400

8. 15 20
8
4
1 3 5 6 30 409
Insertion into a full leaf triggers bottom-up node
splitting pass.
16 17

9.  ai is a pointer to a subtree.
 pi is a dictionary pair.
m a0 p1 a1 p2 a2 …pm am
ceil(m/2)-1 a0 p1 a1 p2 a2 …pceil(m/2)-1 aceil(m/2)-1
m-ceil(m/2) aceil(m/2) pceil(m/2)+1 aceil(m/2)+1 …pm am
• pceil(m/2) plus pointer to new node is inserted in
parent.

10. 15 20
8
4
1 3 5 6 30 409
• Insert a pair with key = 2.
• New pair goes into a 3-node.
16 17

11.  Insert new pair so that the 3 keys are in
ascending order.
• Split overflowed node around middle key.
1 2 3
• Insert middle key and pointer to new node
into parent.
1 3
2

12. 15 20
8
4
1 3 5 6 30 409
• Insert a pair with key = 2.
16 17

13. 15 20
8
4
5 6 30 409 16 17
3
1
2
• Insert a pair with key = 2 plus a pointer into parent.

14. • Now, insert a pair with key = 18.
15 20
8
1
2 4
5 6 30 409 16 173

15.  Insert new pair so that the 3 keys are in
ascending order.
• Split the overflowed node.
16 17 18
• Insert middle key and pointer to new node
into parent.
1816
17

16. • Insert a pair with key = 18.
15 20
8
1
2 4
5 6 30 409 16 173

17. • Insert a pair with key = 17 plus a pointer into parent.
15 20
8
1
2 4
5 6 30 4093
18
16
17

18. • Insert a pair with key = 17 plus a pointer into parent.
8
1
2 4
5 6 30 4093 16
17
15
18
20

19. • Now, insert a pair with key = 7.
1
2 4
5 6 30 4093 16
15
18
20
8 17

20. • Insert a pair with key = 6 plus a pointer into parent.
30 401
2 4
93 16
15
18
20
8 17
5
7
6

21. • Insert a pair with key = 4 plus a pointer into parent.
30 401 93 16
15
18
20
8 17
6
4
2
5 7

22. • Insert a pair with key = 8 plus a pointer into parent.
• There is no parent. So, create a new root.
30 40
1
9
3
16
15
18
20
6
8
2
5 7
4
17

23. • Height increases by 1.
30 401 93 16
15
18
2062
5 7
4 17
8