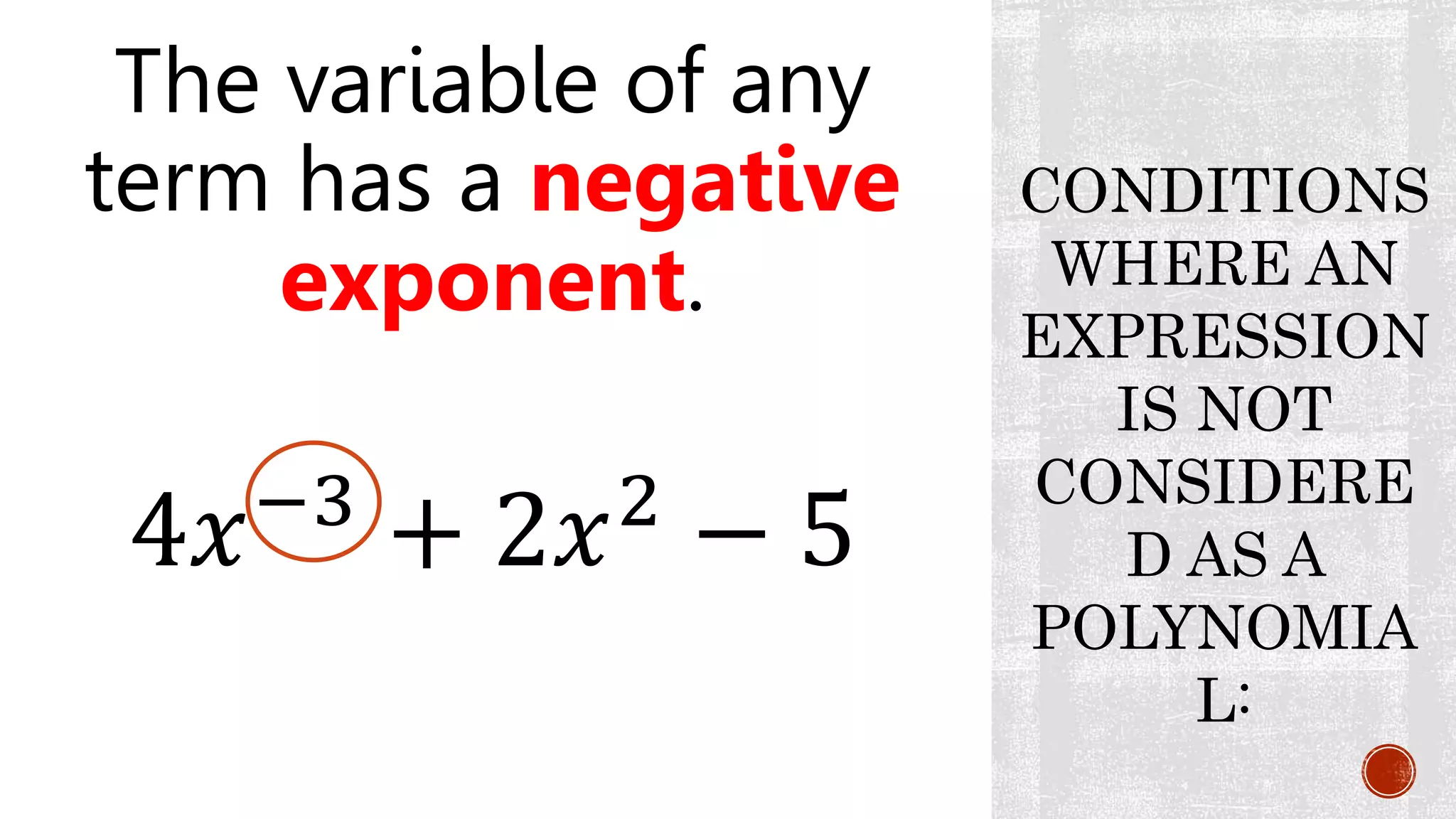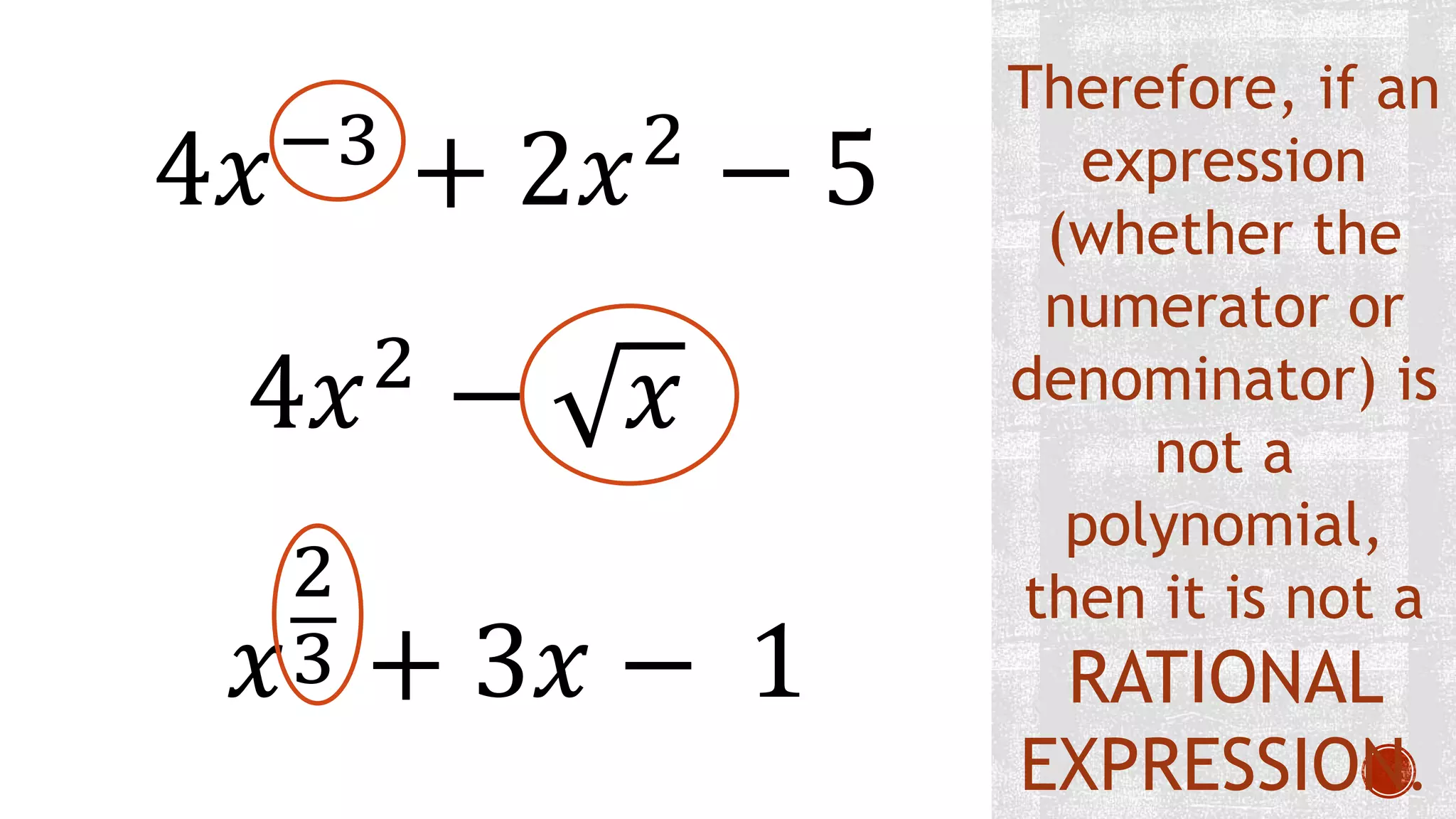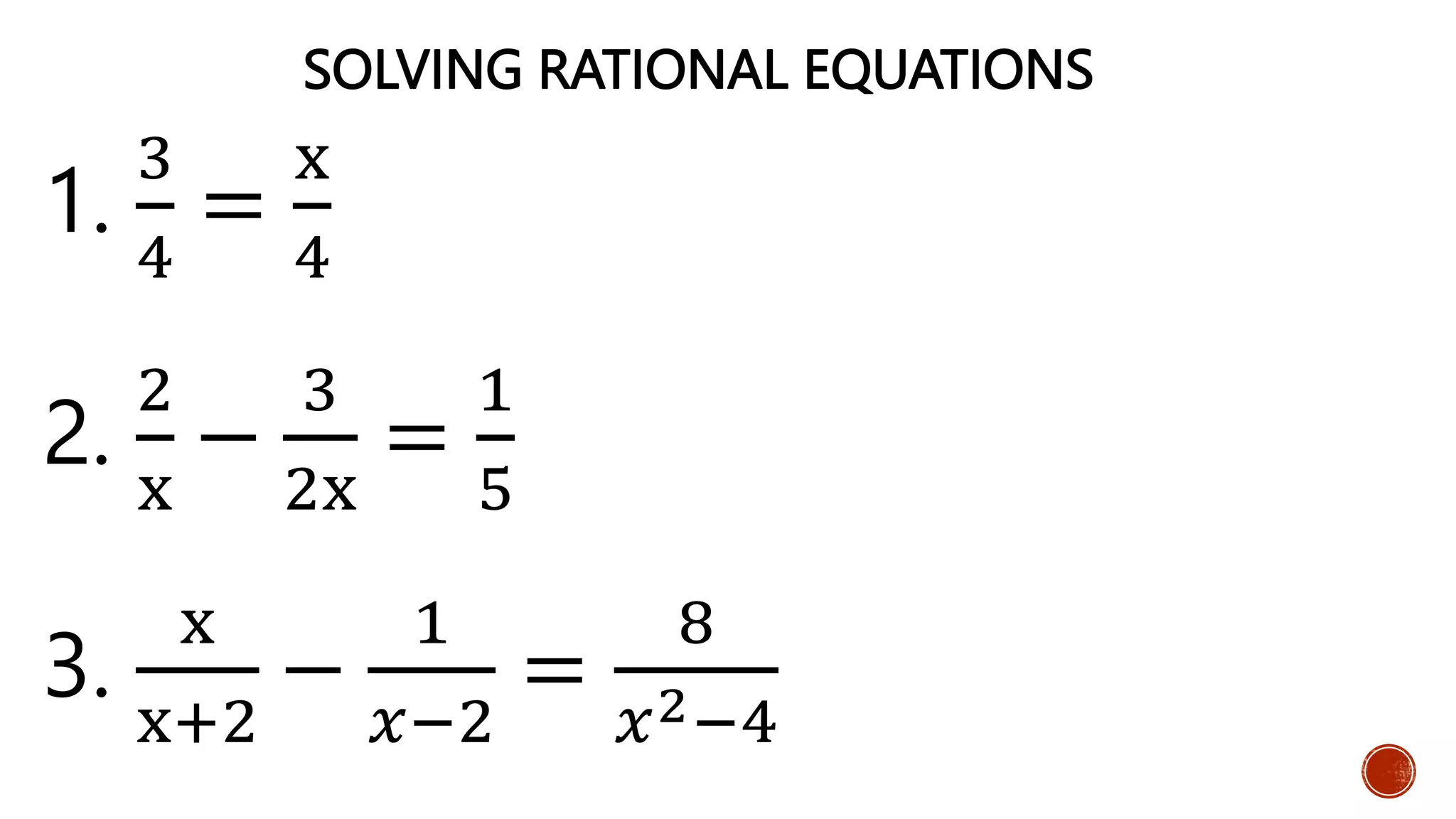Embed presentation
Download to read offline


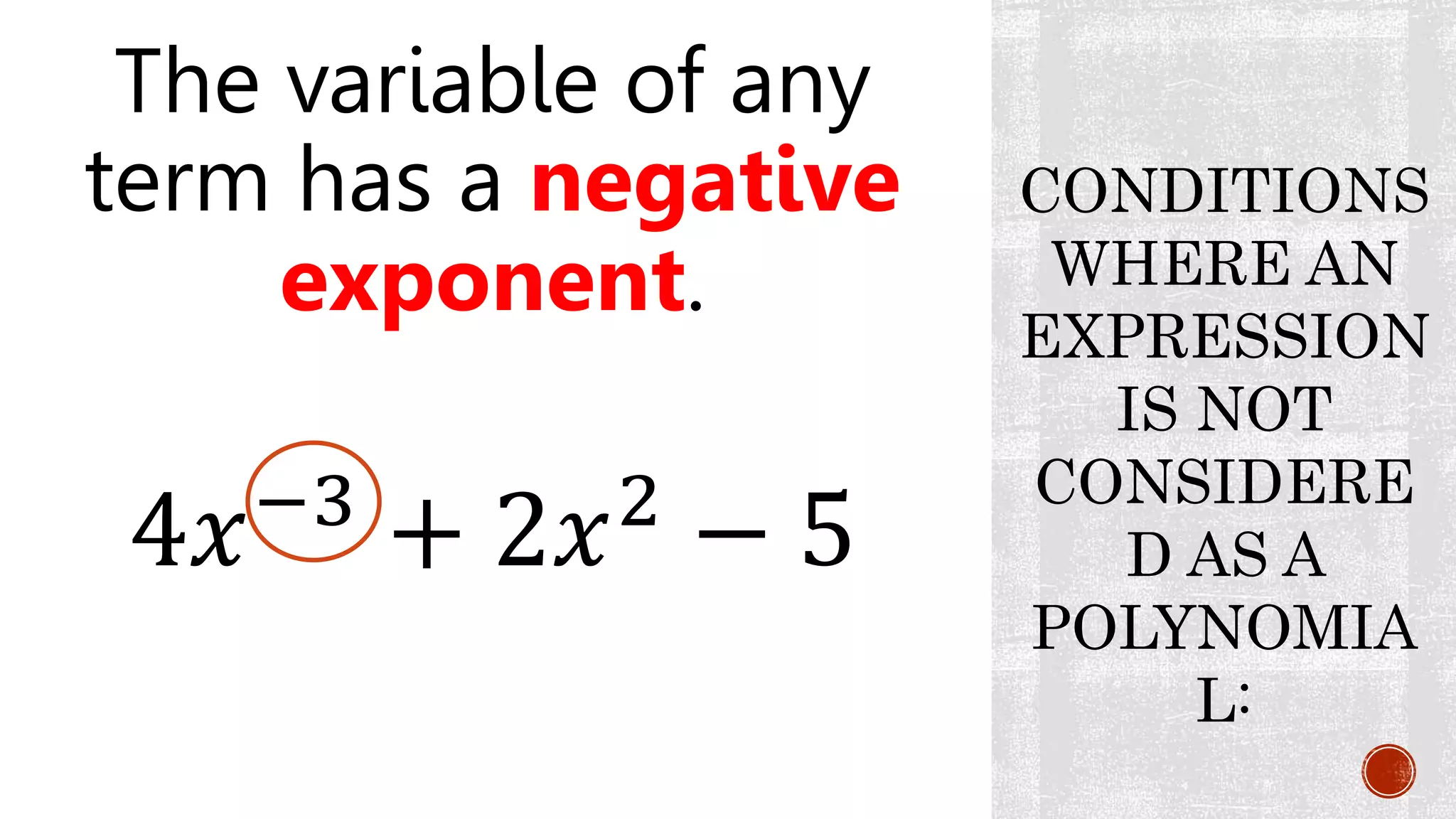


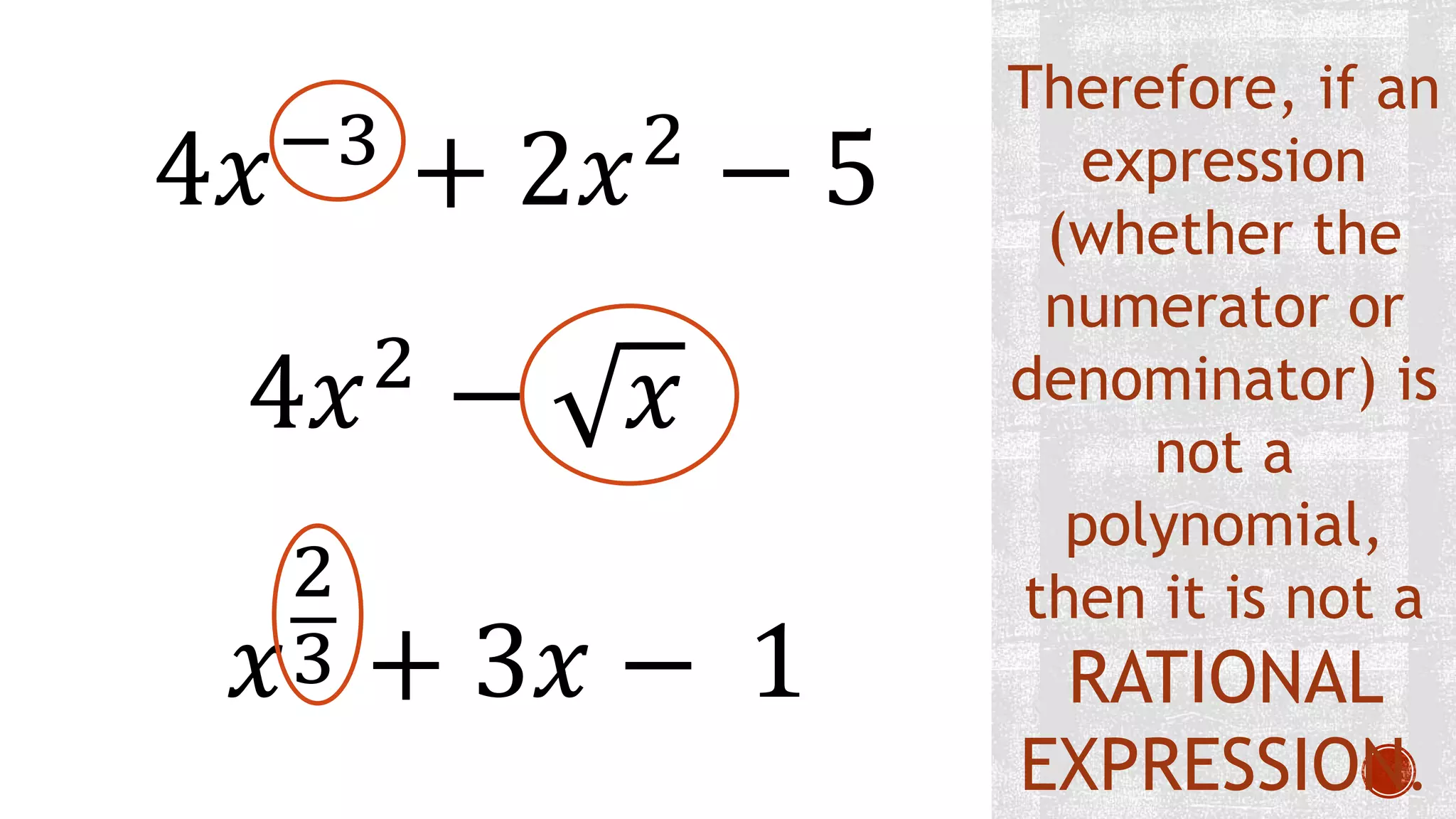
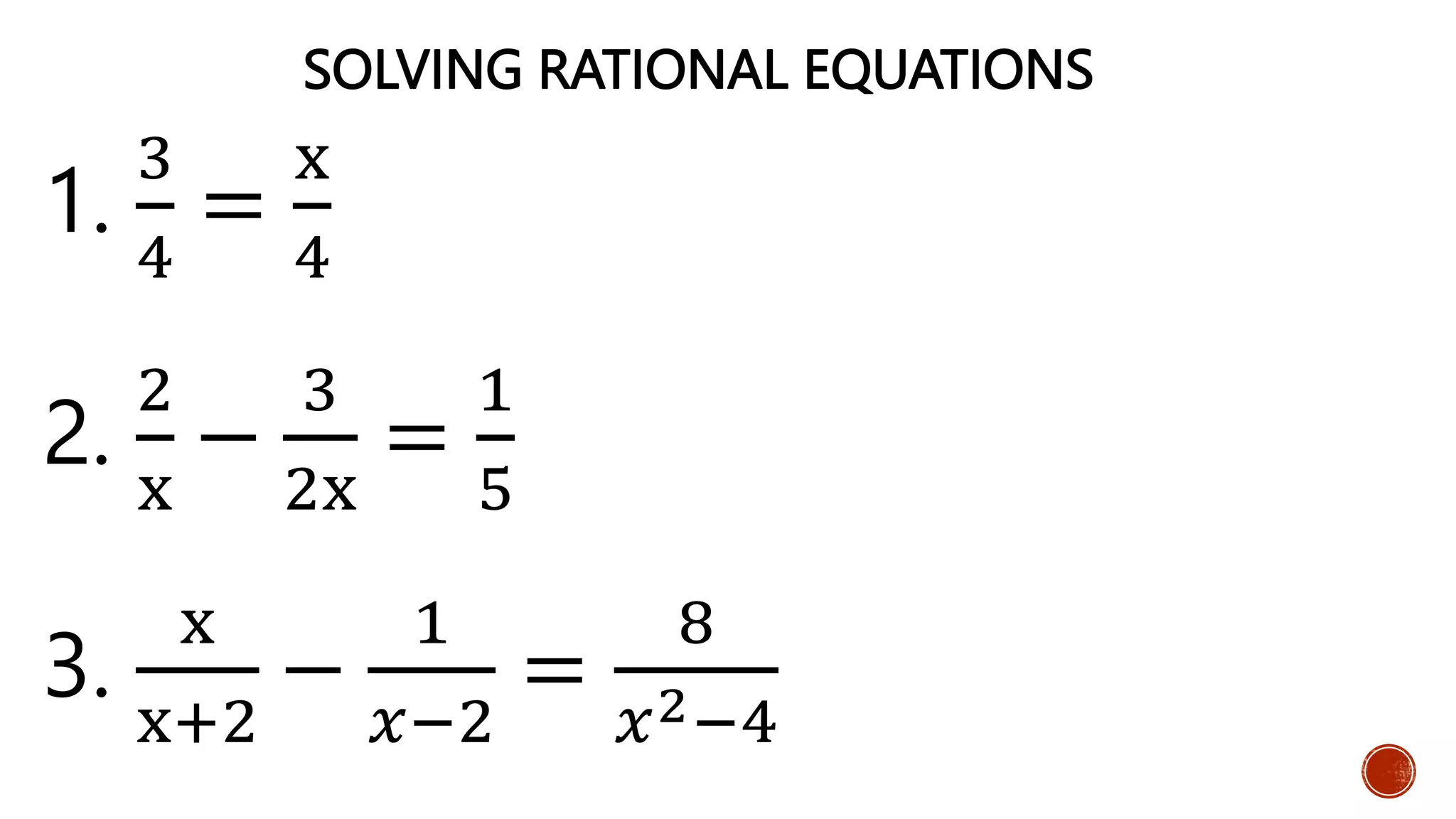
This document defines and provides examples of rational expressions, equations, and inequalities. A rational expression is a ratio of two polynomial expressions. Rational expressions are not considered polynomials if the variables have negative exponents, are inside radical symbols, or have fractional exponents. Rational equations and inequalities involve rational expressions and use equal or inequality symbols. A rational function is an expression of the form f(x) = p(x)/q(x) where p(x) and q(x) are polynomials and q(x) is not equal to zero. Examples of rational equations, inequalities, and functions are provided.
Introduction to rational functions, equations, and inequalities.
Definition of polynomial: expression with variables and coefficients, examples given.
Conditions where an expression is not a polynomial: negative exponent example provided.
Another condition for non-polynomial: variable inside radical symbol.
Condition where variable has a fractional exponent, not a polynomial example provided.
A non-polynomial expression indicates a non-rational expression. Examples clarified.
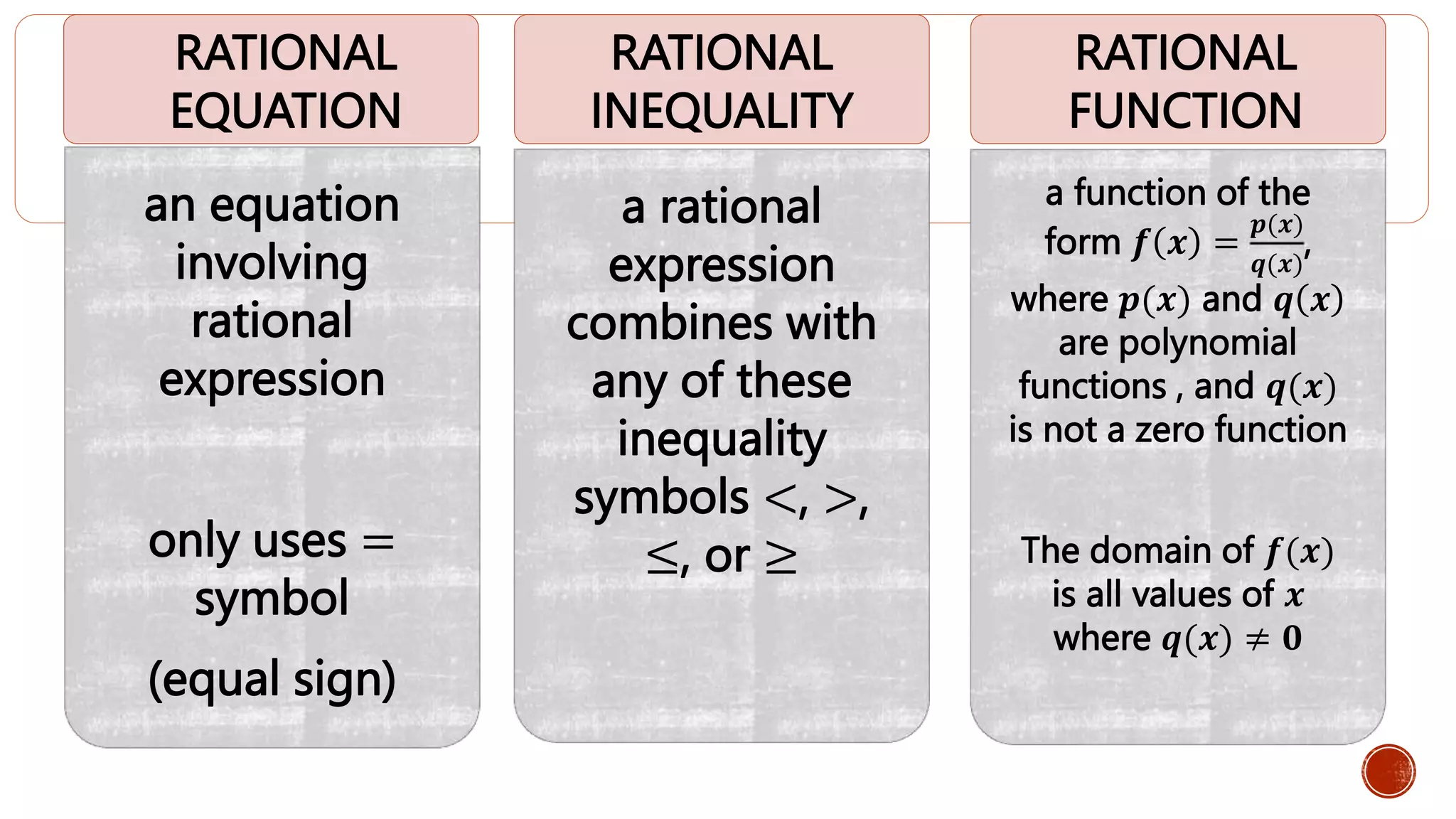
Definition of rational equations and inequalities, including domains of functions.
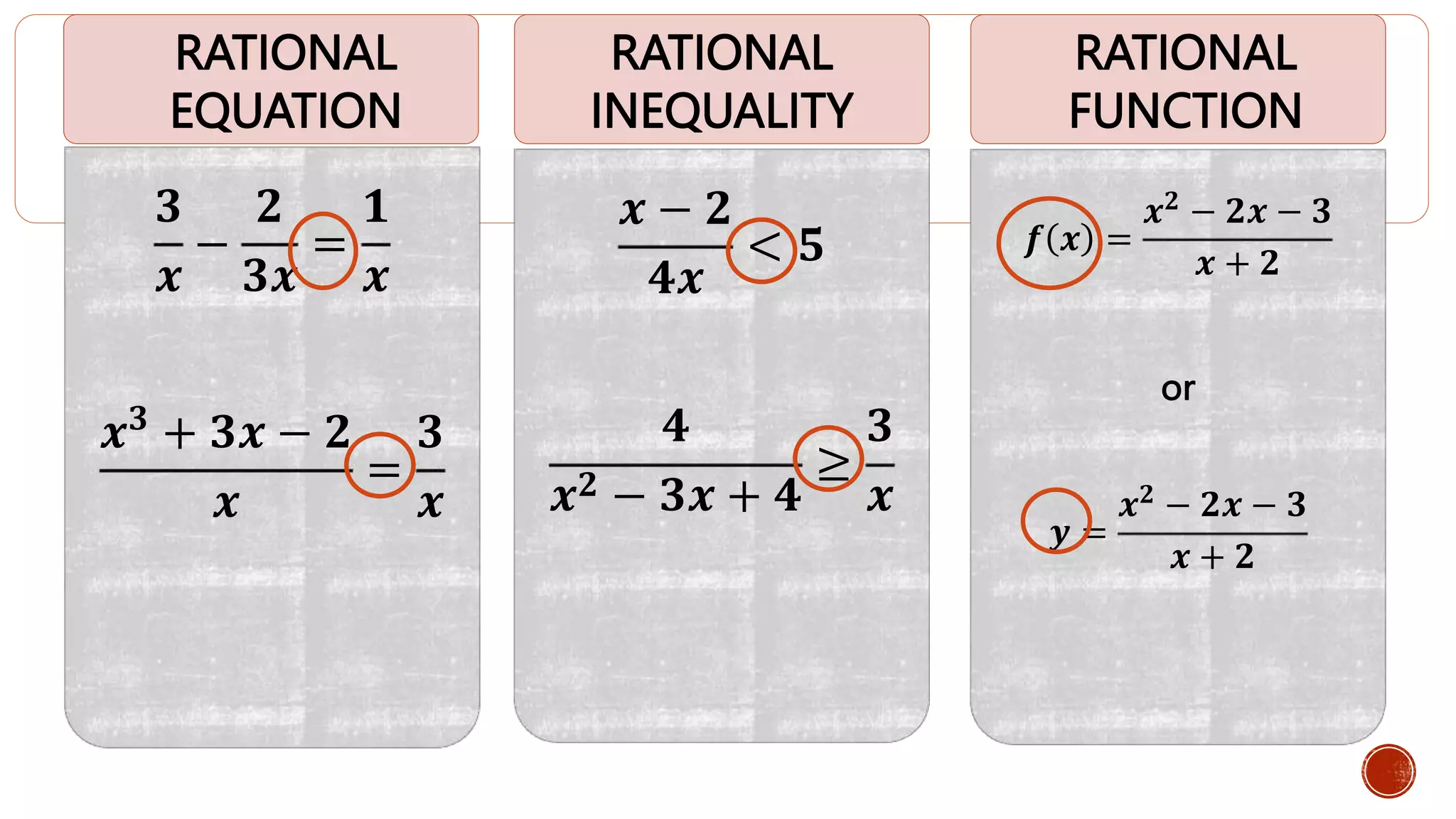
Various rational equations and inequalities are illustrated with equations.
Steps and examples for solving rational equations provided.