This document discusses using R and RStudio to simulate reinforcement learning models. It demonstrates simulating a Rescorla-Wagner model to update action values Q_A and Q_B based on payoffs from actions A and B over time. The model is expanded to select actions stochastically using a softmax function of the difference between Q_A and Q_B. Plots show the evolution of Q_A and Q_B over time for different learning rate and temperature parameters. The document provides an example code implementation of this reinforcement learning model in R.

1. R
Masatoshi Yoshida
2020/12/26
CHAIN 2020 R RStudio
2
RStudio Cloud R markdown knitr html
PDF
R
R “Run”
“Run Current Chunk”
1+2
## [1] 3
“3”
“Run current chunk”
Windows Linix Ctrl+Shift+Enter Mac Command+Shift+Enter
R
knitr::opts_chunk$set(echo = TRUE)
source('functions.R')
library(tidyverse)
## ── Attaching packages ─────────────────────────────────────
── tidyverse 1.3.0 ──
## ggplot2 3.3.2 purrr 0.3.4
## tibble 3.0.4 dplyr 1.0.2
## tidyr 1.1.2 stringr 1.4.0
## readr 1.4.0 forcats 0.5.0
## ── Conflicts ────────────────────────────────────────── ti
dyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()

2. 2 R
2 (1)
A B
A
A 6 B 4
A B 20
A A 1
( )
rnorm(n=1, mean=6, sd=1)
## [1] 6.383498
R
rnorm rnorm 3
(n), (mean), (sd)
6 1 1
A 20 20
n,mean,sd
rnorm(20, 6, 1)
## [1] 5.412230 4.530800 6.951788 5.502108 6.414942 8.257738 6.395087 5.455391
## [9] 8.408270 6.523041 6.156924 5.826539 6.590015 6.505697 5.347838 6.098579
## [17] 7.141431 5.856865 5.309370 6.642150
6

3. payoff_A <- rnorm(20, 6, 1)
mean(payoff_A)
## [1] 6.220117
sd(payoff_A)
## [1] 1.333274
1 rnorm(20, 6, 1) payoff_A payoff_A
mean payoff_A sdn
20 (payoff_A )
(payoff_A <- rnorm(20, 6, 1))
## [1] 5.662120 7.793825 4.590291 6.557083 5.759567 5.834412 6.130306 4.284135
## [9] 7.753249 8.187345 5.071674 7.213497 5.616805 4.234351 6.517725 5.916005
## [17] 5.100752 4.186295 6.442338 4.567008
20 1000
B 1000
set.seed(777) # setting a seed to the random process below to fix the result
payoff_A <- rnorm(1000, 6, 1)
payoff_B <- rnorm(1000, 4, 1)
mean(payoff_A)
## [1] 6.001977
mean(payoff_B)
## [1] 4.010321
1000 rnorm (
)
(6.001977 4.010321) set.seed
777
set.seed
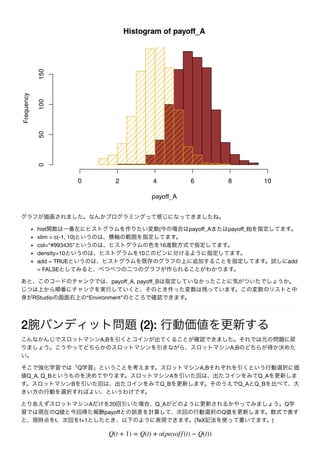
A B
hist(payoff_A, xlim = c(-1, 10), col="#993435")
hist(payoff_B, density=10, col="#edae00", add = TRUE)

4. hist ( payoff_A payoff_B)
xlim = c(-1, 10)
col=“#993435” 16
density=10 10
add = TRUE add
= FALSE
payoff_A, payoff_B
RStudio “Environment”
2 (2):
A,B
A,B
Q A,B
Q_A, Q_B A Q_A
B Q_B Q_A Q_B
A 20 Q_A Q
Q payoff Q
t t+1 (TeX )

5. Rescorla-Wagner
Q_A QA0 = 0 1 A payoff = 6.48
Q_A (=QA1)
QA0 <- 0
payoff <- 6.48
alpha <- 0.5
(QA1 <- QA0 + alpha * (payoff - QA0))
## [1] 3.24
Q_A 0 3.24 0.5
20 A Q_A 20 payoff_A
set.seed(777)
(payoff_A <- rnorm(20, 6, 1))
## [1] 6.489786 5.601459 6.510836 5.601188 7.638686 6.621274 6.202704 7.108938
## [9] 5.793775 5.621035 5.695738 6.054162 4.119069 5.966244 8.311495 6.972340
## [17] 6.964608 5.455867 6.671223 6.500819
Q_A c 20 NA (
) 1 2 A Q_A
(Q_A <- c(rep(NA,20)))
## [1] NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
Q_A 0 1 0 Q_A[1]
1 0
Q_A[1] <- 0
Q_A
## [1] 0 NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA NA
Q_A 0
1 payoff_A 2 Q_A
payoff_A[1]
## [1] 6.489786

6. Q_A[2] <- Q_A[1] + alpha * (payoff_A[1] - Q_A[1])
Q_A
## [1] 0.000000 3.244893 NA NA NA NA NA NA
## [9] NA NA NA NA NA NA NA NA
## [17] NA NA NA NA
2 payoff_A Q_A
payoff_A[2]
## [1] 5.601459
Q_A[3] <- Q_A[2] + alpha * (payoff_A[2] - Q_A[2])
Q_A
## [1] 0.000000 3.244893 4.423176 NA NA NA NA NA
## [9] NA NA NA NA NA NA NA NA
## [17] NA NA NA NA
Q 4.42
A t t
3
t <- 3
Q_A[t+1] <- Q_A[t] + alpha * (payoff_A[t] - Q_A[t])
Q_A
## [1] 0.000000 3.244893 4.423176 5.467006 NA NA NA NA
## [9] NA NA NA NA NA NA NA NA
## [17] NA NA NA NA
t 19 1 for
for (t in 1:19) {
Q_A[t+1] <- Q_A[t] + alpha * (payoff_A[t] - Q_A[t])
}
Q_A
## [1] 0.000000 3.244893 4.423176 5.467006 5.534097 6.586392 6.603833 6.403269
## [9] 6.756103 6.274939 5.947987 5.821863 5.938013 5.028541 5.497392 6.904444
## [17] 6.938392 6.951500 6.203684 6.437453
0 Q_A payoff_A 6

7. set.seed(777)
alpha <- 0.2
payoff_A <- rnorm(20, 6, 1)
Q_A <- c(rep(NA,20))
Q_A[1] <- 0
for (t in 1:19) {
Q_A[t+1] <- Q_A[t] + alpha * (payoff_A[t] - Q_A[t])
}
Q_A
## [1] 0.000000 1.297957 2.158658 3.029093 3.543512 4.362547 4.814292 5.091975
## [9] 5.495367 5.555049 5.568246 5.593745 5.685828 5.372476 5.491230 6.055283
## [17] 6.238694 6.383877 6.198275 6.292865
Q_B Q_A payoff_B 6 4
alpha <- 0.2
payoff_B <- rnorm(20, 4, 1)
Q_B <- c(rep(NA,20))
Q_B[1] <- 0
for (t in 1:19) {
Q_B[t+1] <- Q_B[t] + alpha * (payoff_B[t] - Q_B[t])
}
Q_B
## [1] 0.0000000 0.3938728 1.1606486 1.5719139 2.3122495 2.9373417 3.2352751
## [8] 3.0393288 3.2263998 3.0834555 3.1584492 3.4590219 3.7388860 4.0414425
## [15] 3.7902134 4.1368013 3.8622445 4.2229662 4.0776561 3.9464291
0 Q_B payoff_B 4
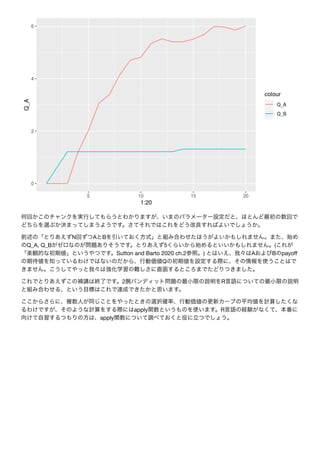
ggplot2 x 1:20, y Q_A
Q_B geom_line
ggplot() +
geom_line(aes(x=1:20, y=Q_A, colour = "Q_A")) +
geom_line(aes(x=1:20, y=Q_B, colour = "Q_B"))

8. 15 payoff Q (= )
2 (3):
A B
( )
Q
payoff_A, Q_A, payoff_B, Q_B
set.seed(777)
alpha <- 0.2
payoff_A <- rnorm(20, 6, 1)
Q_A <- c(rep(NA,20))
Q_A[1] <- 0
payoff_B <- rnorm(20, 4, 1)
Q_B <- c(rep(NA,20))
Q_B[1] <- 0
Q Q if-
else Q_A %%2==0 (%%2 2
0 )
Q_A[t+1] <- Q_A[t] Q_B

9. for (t in 1:19) {
if (t%%2==0){
Q_A[t+1] <- Q_A[t] + alpha * (payoff_A[t] - Q_A[t])
Q_B[t+1] <- Q_B[t]
}
else{
Q_A[t+1] <- Q_A[t]
Q_B[t+1] <- Q_B[t] + alpha * (payoff_B[t] - Q_B[t])
}
}
Q_A
## [1] 0.000000 0.000000 1.120292 1.120292 2.016471 2.016471 2.937432 2.937432
## [9] 3.771733 3.771733 4.141593 4.141593 4.524107 4.524107 4.812534 4.812534
## [17] 5.244496 5.244496 5.286770 5.286770
Q_B
## [1] 0.0000000 0.3938728 0.3938728 0.9584932 0.9584932 1.8543367 1.8543367
## [8] 1.9345781 1.9345781 2.0499981 2.0499981 2.5722611 2.5722611 3.1081425
## [15] 3.1081425 3.5911446 3.5911446 4.0060863 4.0060863 3.8891733
ggplot() +
geom_line(aes(x=1:20, y=Q_A, colour = "Q_A")) +
geom_line(aes(x=1:20, y=Q_B, colour = "Q_B"))

10. 5 A
greedy N ( N=5) Q Q_A
Q_B N Q_A Q_B
N A B
Q 100% Q 95%
5% Q
Q -greedy
% Q_A Q_B
Q_A=6 Q_B=4 A B Q_A=60 Q_B=1
B softmax
softmax Softmax A
1
( logistic softmax logistic
2 softmax logistic )
Q_D <- seq(-3,3,length=101)
beta <- 1
P_A = 1 / (1 + exp(-beta * Q_D))
ggplot() +
geom_line(aes(x=Q_D, y=P_A, colour = "P_A"))

11. seq -3 3 101
0.5 1
0.1 0 Softmax max ( argmax )
softmax Q_A=1.5, Q_B=1.2
Softmax (functions.R) softmax
(RStudio Files functions.R
RWmodel.Rmd editor functions.R
RWmodel.Rmd 30 source(‘functions.R’) functions.R
)
Q_A <- 6
Q_B <- 4
P_A <- softmax(Q_D = Q_A - Q_B, beta = 1)
P_A=0.8807971 P_A sample
x=1 2 P_A P_B(=1-P_A) x=1 A
x=2 B
choice <- sample(x=1:2, size=1, replace=FALSE, prob=c(P_A,1-P_A))
choice
## [1] 1

12. 1 (=A ) 2 (=B )
( 2 (4) )
Q_D <- seq(-3,3,length=101)
P_A1 <- softmax(Q_D, beta = 1)
P_A2 <- softmax(Q_D, beta = 5)
P_A3 <- softmax(Q_D, beta = 99)
ggplot() +
geom_line(aes(x=Q_D, y=P_A1, colour = "beta=1")) +
geom_line(aes(x=Q_D, y=P_A2, colour = "beta=5")) +
geom_line(aes(x=Q_D, y=P_A3, colour = "beta=99"))
100% max
softmax
Q_A Q_B (
)

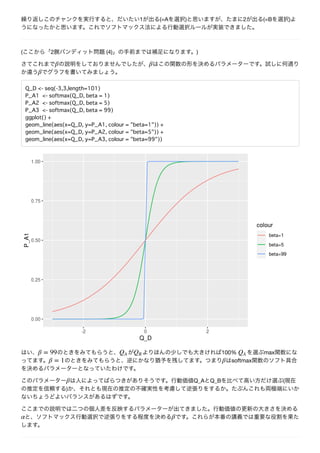
13. 2 (4):
A B
Q_A=0,Q_B=0 A B (
50%-50% ) payoff Q_A Q_B
Q_A,Q_B A B
# �������設定
alpha <- 0.2
beta <- 0.5
# 行動�結果得���payoff������計算����
payoff_A <- rnorm(20, 6, 1)
payoff_B <- rnorm(20, 4, 1)
# 行動価値Q�初期化
Q_A <- c(rep(NA,20))
Q_A[1] <- 0
Q_B <- c(rep(NA,20))
Q_B[1] <- 0
for (t in 1:19) {
# 行動価値Q_A,Q_B�元�行動選択choice�決��
Q_D <- Q_A[t] - Q_B[t]
P_A <- softmax(Q_D, beta)
choice <- sample(x=1:2, size=1, replace=FALSE, prob=c(P_A,1-P_A))
# 行動�結果得���payoff��行動価値Q_A,Q_B�更新
if (choice==1){
Q_A[t+1] <- Q_A[t] + alpha * (payoff_A[t] - Q_A[t])
Q_B[t+1] <- Q_B[t]
}
else{
Q_A[t+1] <- Q_A[t]
Q_B[t+1] <- Q_B[t] + alpha * (payoff_B[t] - Q_B[t])
}
}
ggplot() +
geom_line(aes(x=1:20, y=Q_A, colour = "Q_A")) +
geom_line(aes(x=1:20, y=Q_B, colour = "Q_B"))

14. N A B
Q_A, Q_B 5 (
Sutton and Barto 2020 ch.2 ) A B payoff
Q
2 R
apply R
apply