The document provides a comprehensive guide on using R programming, covering basic calculations such as addition, subtraction, multiplication, and division. It also introduces key concepts like data frames, pie charts, histograms, and statistical functions including summary statistics, quantiles, and regression analysis. Additionally, it includes practical examples for creating plots and performing sampling and probability distributions.

1. BY GROUP B
 Waseem
 Balach
 Salman
 Devika
 Faitma
 Daniyal
 Haneet
 Hajii
 Bashir ahmend
 Gulam Mustafa

2. ADD A FOOTER 2

3. R Studio is that all the information you
need to write code is available in a
single window.
Additionally, with many shortcuts, auto
completion, and highlighting for the
major file types you use while developing
in R, R Studio will make typing easier
and less error-prone.
R offers a wide variety of statistics-
related libraries and provides a
favorable environment for statistical
computing and design.
ADD A FOOTER 3

4. 4
Lets start

5. sum
5
 a=13
 b=15
 c=36
 ## Basic Calculation ##
 ## Addition ##
 Run
 sum=a+b+c
 sum
 Result
 64

6. Subtract
6
 a=13
 b=15
 c=36
 ## Basic Calculation ##
 ## subtract ##
 Run
 Subtract c-b
 Subtract b-a
 Subtract a-c
 subtract
 Result
 21, 15 , -23

7. Multiply
7
 a=13
 b=15
 c=36
 ## Basic Calculation ##
 ## multiply ##
 Run
 Multiply a*b
 Multiply b*c
 Multiply c*a
 multiply
 Result
 195, 540 , 468

8. Divide
8
 a=19
 b=44
 c=89
 ## Basic Calculation ##
 ## multiply ##
 Run
 divide=a/b
 divide=b/c
 divide=c/b
 Divide
 Result
 0.4318182, 0.494382, 2.022727

9. power
9
 ## power ##
 9^4
 199^5
 88990^6
 Run
 Result
 9^4= 6561
 199^5= 312079600999
 88990^6= 4.966463e+29

10. Repetition and sequence
10
##rep()##
 rep(3,10)
Result = 3 3 3 3 3 3 3 3 3 3
• rep(90,9)
result = 90 90 90 90 90 90 90 90 90
##seq()
• Seq (1,100)
= Result
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
[20] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
[39] 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57
[58] 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76
[77] 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
[96] 96 97 98 99 100

11. x = c(20,40,29,10,28,55)
x
names = c("mango","orange","pine","pineapple", "apple")
Names
heartDeck = c(rep(1, 13), rep(0, 39))
heartDeck
Result = 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
11

12. Letters, LETTER, month.abb, month.name
12
Letters
"a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t"
"u" "v" "w" "x" "y" "z"
LETTERS
"A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N" "O" "P" "Q" "R"
"S" "T" [21] "U" "V" "W" "X" "Y" "Z"
month.abb
"Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov"
"Dec“
month.name
"January" "February" "March" "April" "May" "June"
[7] "July" "August" "September" "October" "November"
"December"

13. Data frame
13
A DataFrame is a data structure that organizes data into a 2-
dimensional table of rows and columns, much like a spreadsheet.
DataFrames are one of the most common data structures used in
modern data analytics because they are a flexible and intuitive way of
storing and working with data.
 Numerical=c(1,2,3,4,5)
 Character=c("one","two","three","four","five")
 logical=c(TRUE,FALSE,FALSE,TRUE,TRUE)
 data.frame(Character,Numerical,logical) Character Numerical
logical) 1 one 1 TRUE 2 two 2 FALSE 3
three 3 FALSE 4 four 4 TRUE 5 five 5
TRUE

14. Pie chart
14
Fruits=c ("Mango","pineaplle","apple","banana",
"orange")
slices=c(6,4,7,8,3)
pie(slices,Fruits,main = "pie chart of furits")
#simple pie chart
h=c(1,2,3,4,5)

15. 15
A histogram is a graph used to represent
the frequency distribution of a few data
points of one variable. Which is equal to
class interval.
hist(iris$Sepal.Length)
hist(iris$Petal.Width)
hist(faithful$eruptions)

16. 16
hist(faithful$eruptions, n=10 ,col="red")
hist(faithful$eruptions, n=10 ,col="pink")
hist(faithful$eruptions, n=10 ,col=“green")

17. 17
 histogram(iris$Sepal.Length, breaks=seq(4,8,.25))
 histogram(iris$Sepal.Length, breaks=seq(2,9,.44))
 histogram(iris$Sepal.length, breaks=seq(2,9,.44))

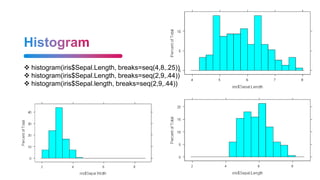
18. It is basically a table where each column is a variable and each row has one
set of values for each of those variables (much like a single sheet in a program
like LibreOffice Calc or Microsoft Excel).
18
Basic
 data("iris")
 names(iris)
Result "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"
 dim(iris)
Result = 150 5
 str(iris3)
 num [1:50, 1:4, 1:3] 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 - attr(*, "dimnames")=List of 3
 ..$ : NULL
 ..$ : chr [1:4] "Sepal L." "Sepal W." "Petal L." "Petal W."
 ..$ : chr [1:3] "Setosa" "Versicolor" "Virginica"

19. 19
 sum(iris$Sepal.Length)
 Result = 876.5
 sum(iris$Sepal.Width)
 result = 458.6
 sum(iris$Petal.Length)
 result = 563.7
 sum(iris$Petal.Width)
 result = 179.9
 IQR(iris$Sepal.Length)
 Result= 1.3
 sort(iris3)
 sort(iris$Sepal.Length)
 round(iris$Sepal.Length)

20. 20
 summary(iris)
• Result
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300
virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
 summary(iris$Sepal.Length)
• Result
Min. 1st Qu. Median Mean 3rd Qu. Max. 4.300 5.100 5.800
5.843 6.400 7.900

21. 21
 sum(iris$Sepal.Length)
 Result = 876.5
 sum(iris$Sepal.Width)
 result = 458.6
 sum(iris$Petal.Length)
 result = 563.7
 sum(iris$Petal.Width)
 result = 179.9
 IQR(iris$Sepal.Length)
 Result= 1.3

22. 22
 mean(x, na.rm = T)
Result 30.33333
 median(x,na.rm=T)
Result 28.5
 summary(x)
result Min. 1st Qu. Median Mean 3rd Qu. Max.
10.00 22.00 28.50 30.33 37.25 55.00 >
 sd(x,na.rm=T)
result 15.68014
 var(x,na.rm=T)
Result 245.8667

23. 23
A quantile defines a particular part of a data set, i.e. a quantile determines how many values in
a distribution are above or below a certain limit
 quantile(x, probs = seq(0,1,.2), na.rm=T)
0% 20% 40% 60% 80% 100%
10 20 28 29 40 55
 quantile(x, probs = seq(0,1,.3), na.rm=T)
 0% 30% 60% 90%
 10.0 24.0 29.0 47.5
 quantile(x, probs = seq(0,1,.4), na.rm=T)
 0% 40% 80%
 10 28 40
 quantile(x, probs = seq(0,1,.6), na.rm=T)
 0% 60%
 10 29
 quantile(x, probs = seq(0,1,.9), na.rm=T)
 0 0% 90% 10.0 47.5

24. 24
An integer (pronounced IN-tuh-jer) is a whole number (not a fractional number) that can be
positive, negative, or zero. Examples of integers are: -5, 1, 5, 8, 97,
 firstTwentyIntegers = 1:30
 sum(firstTwentyIntegers)
 Result = 465

25. 25
##binary ##
dec="x"=20:30
20:30
Result = 20 21 22 23 24 25 26 27 28 29 30
dec="x"=50:90
50:90
Results 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
65 66 67 68 69 70 71 72 73 74 75
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

26.  boxplot(iris$Sepal.Length)
 boxplot(iris$Sepal.Length,
col="orange")
 boxplot(Sepal.Length ~
Species, data=iris,
col="yellow", ylab="Sepal
length",main="Iris Sepal
Length by Species")

27. Plot = plot(iris)

28. ADD A FOOTER 28
plot(iris$Sepal.Length) plot(iris$Petal.Length)

29. ADD A FOOTER 29
plot(waiting~eruptions,data=faithful) plot(waiting~eruptions,data=faithful)

30. ADD A FOOTER 30
plot(waiting~eruptions,data=faithful, cex=5) plot(waiting~eruptions,data=faithful, cex=10)

31. ADD A FOOTER 31
plot(waiting~eruptions,data=faithful, pch=5)
plot(waiting~eruptions,data=faithful, pch=50)

32. plot(waiting~eruptions,data=faithful,
cex=5,pch=19,col="yellow")
plot(waiting~eruptions,data=faithful,
cex=5,pch=19,col="red", main="Old Faithful Eruptions",

33. Regression, correlation
 #regression
 y=c(70,65,90,95,110,45,120,140,155,150)
 x=c(80,100,120,140,160,180,200,220,240,280)
 lm(y~x)
Call:
 lm(formula = y ~ x)
 Coefficients:
 (Intercept) x
 24.7944 0.4605
 #correclation
 y=c(70,65,90,95,110,45,120,140,155,150)
 x=c(80,100,120,140,160,180,200,220,240,280)
 cor(x,y)
 0.7843481

34. sample
• sample(c("Heads","Tails"), size=1)
• Result = "Tails"
• sample(c("Heads","Tails"), size=2)
• "Tails" "Heads"
• sample(c("Heads","Tails"),
• "Heads" "Tails" "Tails" "Tails" "Heads" "Heads" "Heads" "Tails" "Tails" "Heads"
• size=10, replace=T)
• sample(c(0, 1), 10, replace = T)
• 1 1 1 1 1 1 1 1 1 1
• sample(c(0, 5), 10, replace = T)
• 5 0 0 0 0 0 0 5 5 0

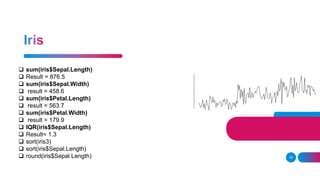
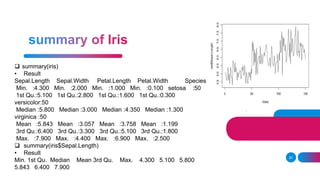
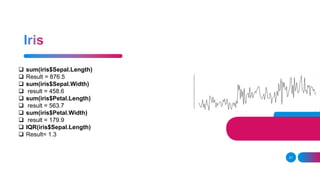
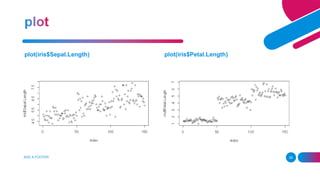
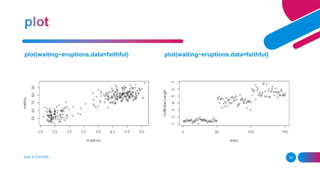
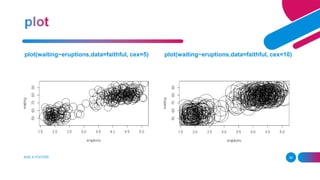
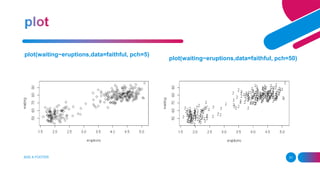
35. replicate
 sample(c("heads","TAILS"), 2, replace = T)
Result "TAILS" "heads"
 replicate(5, sample(c("Heads","TAILS"), 2, replace =T))
Result [,1] [,2] [,3] [,4] [,5]
 [1,] "Heads" "Heads" "Heads" "Heads" "Heads"
 [2,] "Heads" "Heads" "Heads" "Heads" "Heads"
 replicate(10, sample(c("Heads","TAILS"), 2, replace =T))
Result

36. dbinom
 dbinom(0, 5, .5) #probabilty of 0 heads in 5 flips
Result 0.03125
 dbinom(0:5, 5, .5) #full probability dist. for 5 flips
 Result 0.03125 0.15625 0.31250 0.31250 0.15625 0.03125
 sum(dbinom(0:2, 5, .5)) #probability of 2 or fewer heads in 5
flips
Result 0.5
 sum(dbinom(0:8, 9, .10)) #probability of 6 or fewer heads in 8
flips
 Result 1

37. rbinom, binom.test, prop.test
pbinom(2, 5, .5) #same as last line
Result 0.5
table(rbinom(10000, 5, .5)) / 10000
Result 0 1 2 3 4 5
0.0335 0.1544 0.3131 0.3182 0.1532 0.0276
binom.test(29,200, .21)
Result Exact binomial test
data: 29 and 200
number of successes = 29, number of trials = 200, p-value = 0.02374
alternative hypothesis: true probability of success is not equal to 0.21
95 percent confidence interval:
0.09930862 0.20156150
sample estimates:
probability of success
0.145
prop.test(29, 200, .21)

38. #par()
par(nfrow= c(1,2))
poisSamp= rpois(50,3)
maxX = max(poisSamp)
hist(poisSamp)
Par over flow

39. dpois(2:7, 4.2) #probabilities of 2,3,4,5,6,or7
result 0.13226099 0.18516538 0.19442365 0.16331587 0.11432111 0.06859266
ppois(1, 9.2) #probabilities of 1 or fewer successes in pois(4.2); sameas sum (0:1,4.2
Result 0.001030602
1-ppois(7,4.2) #probability of 8 or more successes in pois(4.2)
0.001030602
dpois(), ppois()

40. data(warpbreaks)
by(warpbreaks$breaks, warpbreaks$tension, mean)
warpbreaks$tension: L
[1] 36.38889
---------------------------------------------------------------
warpbreaks$tension: M
[1] 26.38889
---------------------------------------------------------------
warpbreaks$tension: H
[1] 21.66667
by

41. t.test(extra ~ group, data=sleep) # 2-sample t with group id column
Result
Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.07939
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean in group 1 mean in group 2
0.75 2.33
data(sleep)

42. t.test(sleepGrp1, sleepGrp2, conf.level=.99)
Welch Two Sample t-test
data: sleepGrp1 and sleepGrp2
t = -1.8608, df = 17.776, p-value = 0.07939
alternative hypothesis: true difference in means is not equal to 0
99 percent confidence interval:
-4.0276329 0.8676329
sample estimates:
mean of x mean of y
0.75 2.33
data(sleep)

43. Two sample test
Two-sample t test power calculation
n = 40
delta = 0.5
sd = 0.4
sig.level = 0.01
power = 0.998096
alternative = two.sided
NOTE: n is number in *each* group

44. 44