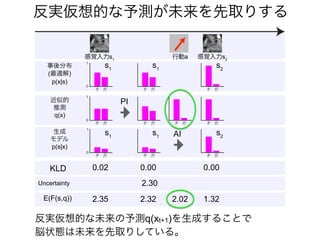
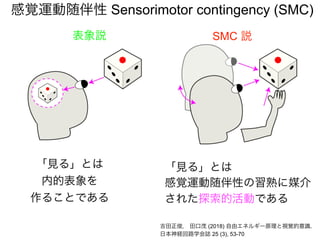
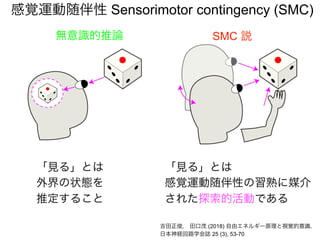
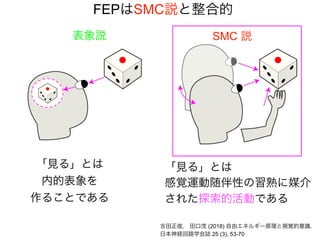
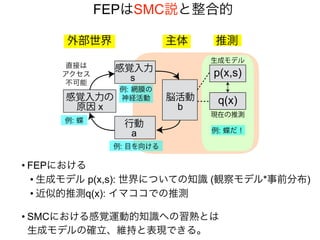
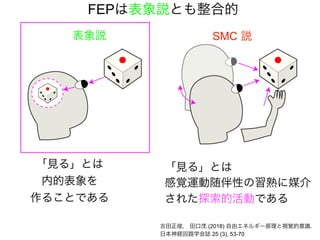
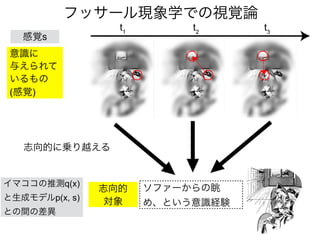
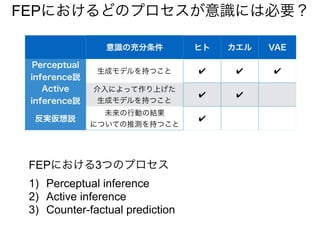
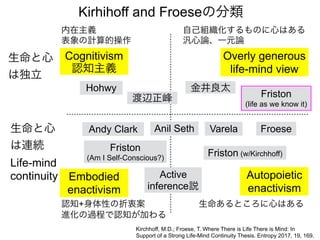
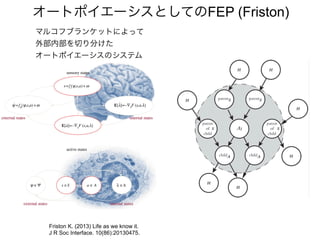
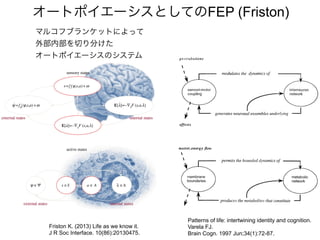
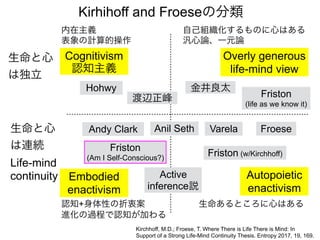
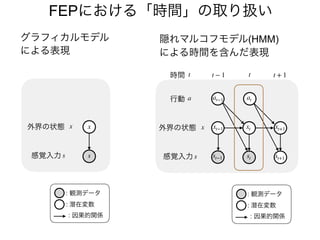
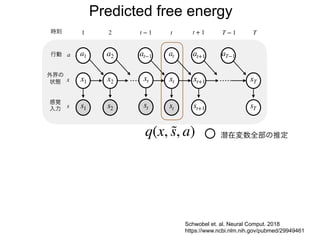
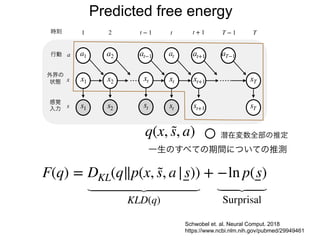
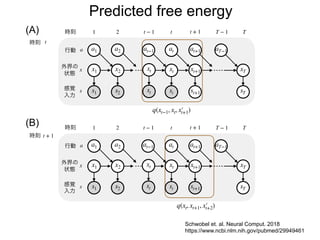
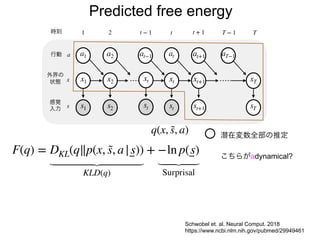
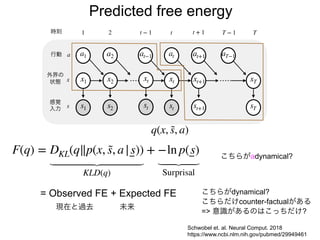
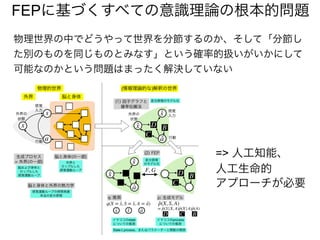
先日シンギュラリティサロン @東京 第31回公開講演会 https://peatix.com/event/676133/ で発表した「自由エネルギー原理と視覚的意識」にアップデートを加えたものを作成しました。内容としては2/14にアップロードした「自由エネルギー原理と視覚」https://speakerdeck.com/pooneil68/fep-and-visual-consciousness-2019-02-14 のアップデート版ですが、こちらを最新版としてご利用ください。このスライドはブログ記事に埋め込む予定。ブログ記事へのリンクはこちら:http://pooneil.sakura.ne.jp/archives/permalink/001673.php






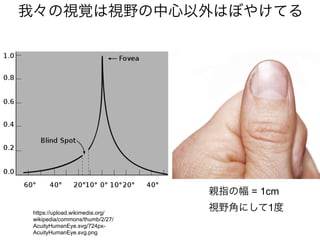













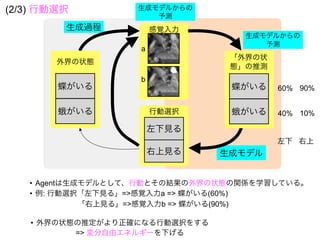

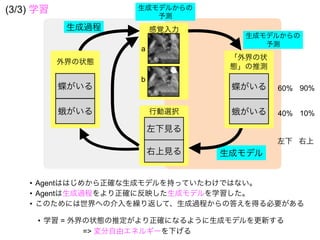






![外界 Agent
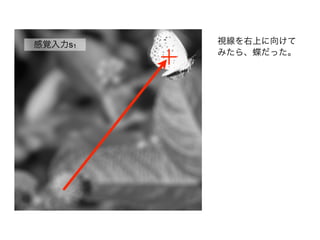
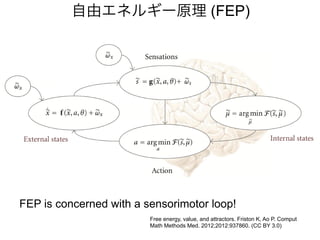
感覚入力
蝶がいる
外界の状態
蛾がいる
「外界の状
態」の推測
蝶がいる
蛾がいる
観測データ, 結果
隠れ値, 原因 内部状態
x = 1
x = 0
x
s
p(x|s)
x = 1
x = 0
s = 1
s = 0
0.9
0.1
0.9
0.1
0.5
0.5
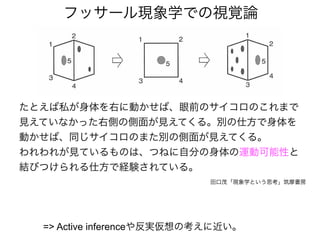
知覚のモデル1: (フル)ベイズ
ベイズの公式
事後分布
=
[
0.9 0.1
0.1 0.9]
x = 1 x = 0
s = 1
s = 0
p(x|s) =
p(x, s)
∑x
p(x, s)
生成モデル
p(s|x)
p(x)
p(x, s)
事前分布 観測モデル
[
0.9 0.1
0.1 0.9]
[0.5 0.5]
[
0.45 0.05
0.05 0.45]
x = 1 x = 0
s = 1
s = 0](https://image.slidesharecdn.com/20190608speakerdeck-220822060452-6c9c5c52/85/2019-06-08-43-320.jpg)
![外界 Agent
感覚入力
蝶がいる
外界の状態
蛾がいる
「外界の状
態」の推測
蝶がいる
蛾がいる
観測データ, 結果
隠れ値, 原因 内部状態
x = 1
x = 0
x
s
p(x|s)
x = 1
x = 0
s = 1
s = 0
0.9
0.1
0.9
0.1
0.5
0.5
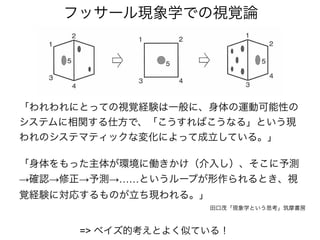
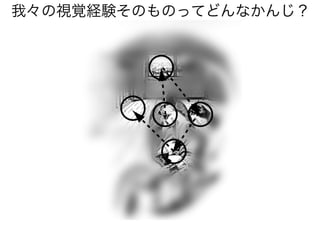
知覚のモデル1: (フル)ベイズ
ベイズの公式
事後分布
=
[
0.9 0.1
0.1 0.9]
x = 1 x = 0
s = 1
s = 0
90%
10%
「s=1」
を観測
p(x|s) =
p(x, s)
∑x
p(x, s)](https://image.slidesharecdn.com/20190608speakerdeck-220822060452-6c9c5c52/85/2019-06-08-44-320.jpg)
![外界 Agent
感覚入力
蝶がいる
外界の状態
蛾がいる
「外界の状
態」の推測
蝶がいる
蛾がいる
観測データ, 結果
隠れ値, 原因 内部状態
x = 1
x = 0
x
s
p(x|s)
x = 1
x = 0
s = 1
s = 0
0.9
0.1
0.9
0.1
0.5
0.5
知覚のモデル1: (フル)ベイズ
ベイズの公式
事後分布
=
[
0.9 0.1
0.1 0.9]
x = 1 x = 0
s = 1
s = 0
90%
10%
「s=1」
を観測
p(x|s) =
p(x, s)
∑x
p(x, s)
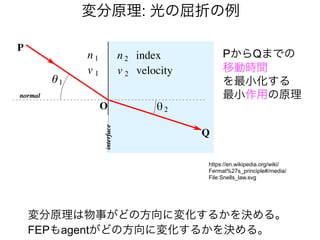
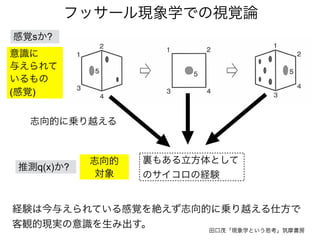
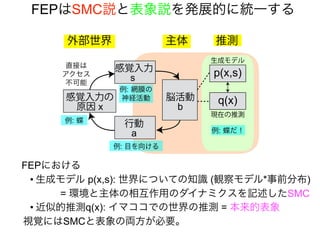
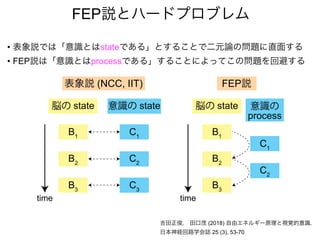
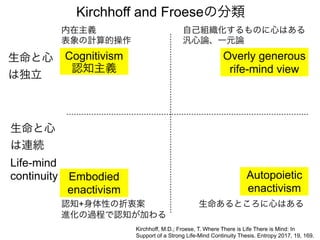
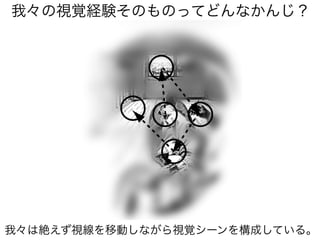
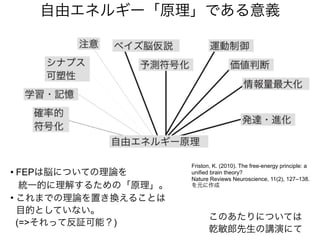
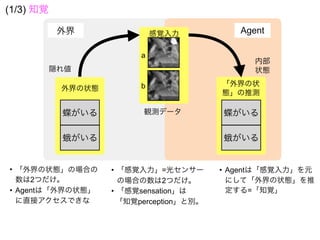
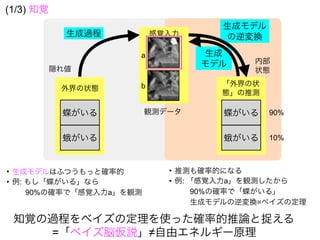
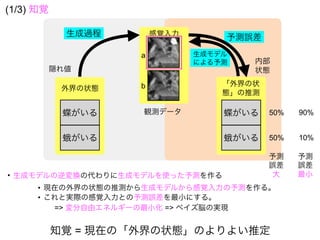
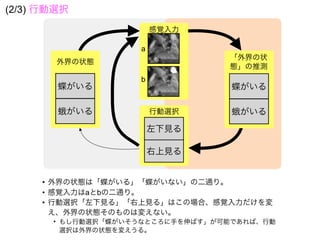
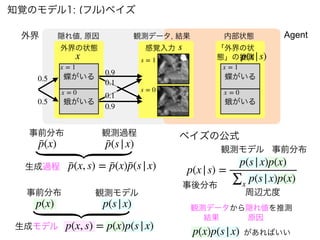
知覚とは
生成モデルと感覚入力に基づいて
外界の状態の事後分布を
計算(確率的に推定)すること => ベイズ脳仮説
事後分布を計算するには
生成モデル(これまでの経験)
と感覚入力(イマココでの観測)
があればいい](https://image.slidesharecdn.com/20190608speakerdeck-220822060452-6c9c5c52/85/2019-06-08-45-320.jpg)



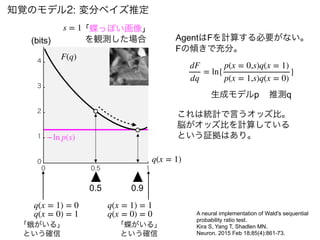
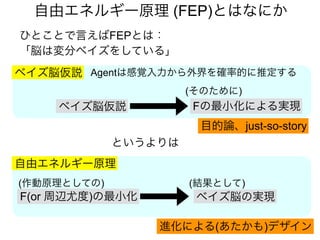
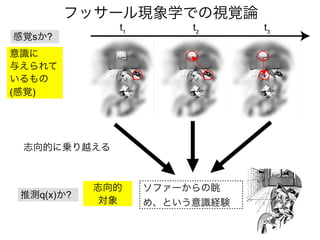
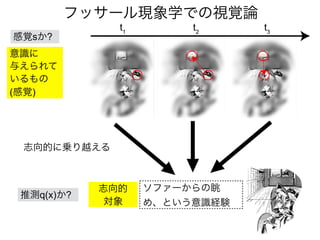
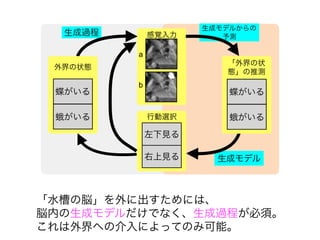
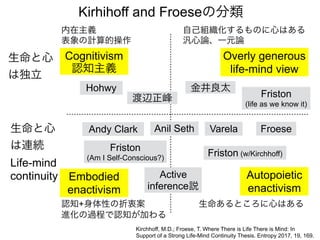
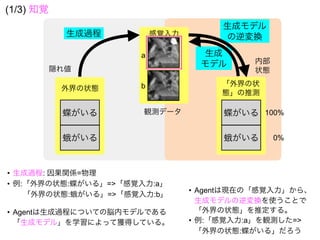
![知覚のモデル2: 変分ベイズ推定
では、q(x)= [1,0]~[0,1]の範囲でFをプロットしてみよう
F(q) =
∑
x
{q(x)ln
q(x)
p(x, s)
}
= DKL(q(x)∥p(x|s)) −ln p(s)
周辺尤度
事後分布
KLD
変分自由エネルギーF
推測
KLD: 推測q(x)と事後分布p(x|s)のKL距離。
KL 距離: 2つの確率分布間の類似度(>=0)
DKL(A(x)kB(x))
=
X
i
A(xi) log
A(xi)
B(xi)
3.22
(bit)
0.29 0.00
A B
x
F(q) = −ln p(s)
推測q(x)が事後分布p(x|s)を完全に近似できたとき、KLD=0が成り立つので](https://image.slidesharecdn.com/20190608speakerdeck-220822060452-6c9c5c52/85/2019-06-08-49-320.jpg)
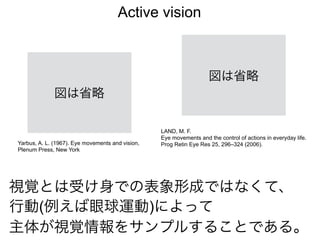
![知覚のモデル2: 変分ベイズ推定
(bits)
q(x = 1)
0.9
0.5
F(q)
−ln p(s)
s = 1「蝶っぽい画像」
を観測した場合
q(x = 1) = 0
q(x = 0) = 1
q(x = 1) = 1
q(x = 0) = 0
「蛾がいる」
という確信
「蝶がいる」
という確信
q(x = 1)
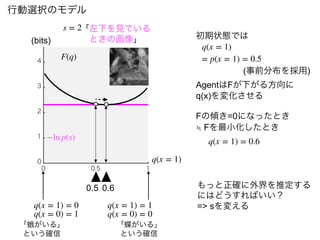
初期状態では
= p(x = 1) = 0.5
(事前分布を採用)
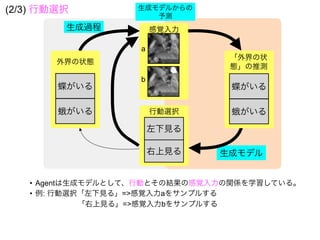
AgentはFが下がる方向に
q(x)を変化させる
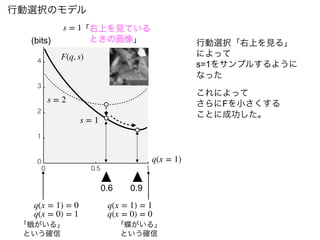
事後分布を近似できている
Fの傾き=0になったとき
≒ Fを最小化したとき
q(x = 1) = 0.9
= p(x|s = 1)
p(x|s) =
[
0.9 0.1
0.1 0.9]
x = 1 x = 0
s = 1
s = 0](https://image.slidesharecdn.com/20190608speakerdeck-220822060452-6c9c5c52/85/2019-06-08-50-320.jpg)