1. 約数
 原案、問題文：宮村
 解答：宮村、橋本
 解説：宮村

2. 問題概要
 数列からなるべく大きい部分集合を選びたい
 ただしどの 2 つを選んでも一方がもう一方の約数
にならないようにしなければならない
 そのような部分集合で添字が辞書順最小のものを
求める問題
 数列の長さ N≦100

3. 辞書順最小を求める問題
 辞書順最小の何かを求める問題を解く典型パター
ンとは
 bool 値を返す判定関数を用意して、列の先頭から
小さい順に候補を試し、 true が帰ってきた時点で
確定して 1 文字進める
 この問題でも同じような考え方を用いる

4. 辞書順最小を求める問題
 辞書式順序云々は無視して、「どれだけ大きい部分
集合を作れるか」という int 値を返す関数を用意
する
 後は、先頭から順に「この数字を部分集合に含め
る場合どれだけ大きい集合が作れるか」と「含め
ないときどれだけ大きい集合が作れるか」の値を
比較して大きい方を選ぶ ( 等しいときは含める )

5. 最大いくつ選べるか
 結局、辞書式順序は無視して最大いくつ選べるか
が分かれば十分であることが分かった
 じゃあ、どうやってそれを求めるのか？
 ところで、 a が b の倍数であるとき a から b へ辺を
張る。このときグラフは DAG になる
 この問題はそのグラフで最大独立点集合 ( のよう
なもの ) の個数を求める問題だと言い換えること
ができる

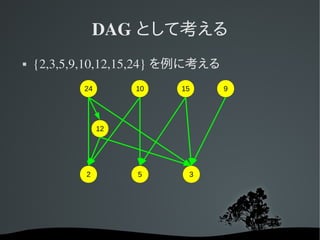
6. DAG として考える
 {2,3,5,9,10,12,15,24} を例に考える
24 10 15 9
12
2 5 3

7. Dilworth の定理
 実は、今回の問題に対する有名な定理が存在する
 Dilworth の定理
推移的に得られる辺を付け加えた DAG に対して
以下の等式が成立する。
( 任意の 2 点間にパスが存在しないような頂点の
部分集合の最大サイズ )
= ( 最小パス被覆の本数 )

8. DAG の最小パス被覆
 典型問題です。プログラミングコンテストチャレンジ
ブックでも紹介されています
 頂点 V と V' を用意する。
頂点 x から y への辺が存在するとき x と y' の間
に辺を張る。
このとき、
|V| ­ |V+V' を頂点とする二部グラフの最大マッチ
ング | = | 最小パス被覆 |

9. 計算量
 DAG の最小パス被覆を求めるのにどれだけかか
るか
­ グラフの構成 O(N^2) 、マッチング O(N^3)
­ マッチングは頑張ればもっと計算量を落とせる
 1 文字ずつ繰り返すので全体の計算量は O(N^4)
 係数が小さいので十分間に合う

10. 解答例
 宮村
C++ : 119 行 2026 byte
Java : 91 行 1792 byte
 橋本
C++ : 105 行 2055 byte