The document covers the Quicksort algorithm, a divide-and-conquer sorting method that efficiently sorts an array by partitioning elements around a pivot. Originating from Tony Hoare's work in 1959, it has an average time complexity of O(n log n), requiring minimal memory as it operates in place. It details the steps of partitioning and recursive sorting of sub-arrays, culminating in a sorted array.

1. COMP0005 (Algorithms)
Quicksort
Vasileios Lampos
Computer Science, UCL
@lampos
lampos.net www
Slides (with potential revisions)
lampos.net/slides/quicksort2019.pdf

2. About this lecture
• Quicksort (yet another sorting algorithm)
— Description
— Performance analysis
• Material
— Cormen, Leiserson, Rivest and Stein. Introduction
to Algorithms. MIT Press, 3rd Edition, 2009
(mainly Chapter 7)
— Alternative slides at https://algs4.cs.princeton.edu/lectures/
(Sedgewick and Wayne)

3. Quicksort divides & conquers

4. Given an array A with n elements, A[1…n]:
• DIVIDE (step 1)
Partition, i.e. re-arrange the elements of, array A[1…n] so that
for some element A[q]:
1. all elements on the left of A[q], i.e. A[1…q−1], are less than or
equal to A[q], and
2. all elements on the right of A[q], i.e. A[q+1…n], are greater
than or equal to A[q].
Quicksort divides & conquers

5. Given an array A with n elements, A[1…n]:
• DIVIDE (step 1)
Partition, i.e. re-arrange the elements of, array A[1…n] so that
for some element A[q]:
1. all elements on the left of A[q], i.e. A[1…q−1], are less than or
equal to A[q], and
2. all elements on the right of A[q], i.e. A[q+1…n], are greater
than or equal to A[q].
• CONQUER (step 2)
Sort sub-arrays A[1…q−1] and A[q+1…n] by recursive
executions of step 1.
Quicksort divides & conquers

6. Given an array A with n elements, A[1…n]:
• DIVIDE (step 1)
Partition, i.e. re-arrange the elements of, array A[1…n] so that
for some element A[q]:
1. all elements on the left of A[q], i.e. A[1…q−1], are less than or
equal to A[q], and
2. all elements on the right of A[q], i.e. A[q+1…n], are greater
than or equal to A[q].
• CONQUER (step 2)
Sort sub-arrays A[1…q−1] and A[q+1…n] by recursive
executions of step 1.
• COMBINE (step 3)
Just by joining the sorted sub-arrays we obtain a sorted array.
Quicksort divides & conquers

7. Given an array A with n elements, A[1…n]:
• DIVIDE (step 1)
Partition, i.e. re-arrange the elements of, array A[1…n] so that
for some element A[q]:
1. all elements on the left of A[q], i.e. A[1…q−1], are less than or
equal to A[q], and
2. all elements on the right of A[q], i.e. A[q+1…n], are greater
than or equal to A[q].
• CONQUER (step 2)
Sort sub-arrays A[1…q−1] and A[q+1…n] by recursive
executions of step 1.
• COMBINE (step 3)
Just by joining the sorted sub-arrays we obtain a sorted array.
Quicksort divides & conquers
Note:
• We will assume that the
elements of A are distinct.
• We will be sorting the elements
of A in an ascending order.

8. Quicksort was…
• invented by Tony Hoare in 1959
• published in 1961 (paper)
from Wikipedia

9. Quicksort was…
• invented by Tony Hoare in 1959
• published in 1961 (paper)
from Wikipedia

10. Quicksort was…
• invented by Tony Hoare in 1959
• published in 1961 (paper)
from Wikipedia
that was the
entire paper!

11. Quicksort was…
• invented by Tony Hoare in 1959
• published in 1961 (paper)
• published with an analysis in 1962 (paper)
from Wikipedia
that was the
entire paper!

12. Quicksort was…
• invented by Tony Hoare in 1959
• published in 1961 (paper)
• published with an analysis in 1962 (paper)
from Wikipedia
that was the
entire paper!

13. Quicksort…
• is still being used (in principle, i.e. its
optimised versions)
from Wikipedia

14. Quicksort…
• is still being used (in principle, i.e. its
optimised versions)
• is efficient
— O(n logn) on average
— Θ(n logn) best case
— Θ(n2) worst case
(for an array with n elements)
from Wikipedia

15. Quicksort…
• is still being used (in principle, i.e. its
optimised versions)
• is efficient
— O(n logn) on average
— Θ(n logn) best case
— Θ(n2) worst case
(for an array with n elements)
• requires a small amount of memory
(in-place algorithm)
from Wikipedia

16. Quicksort7.1 Description of quicksort
Combine: Because the subarrays are already
them: the entire array AŒp : : r is now sort
The following procedure implements quicksor
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
p r
… 6 5 1 … 22 9 2 …
}sub-array A[p…r]
both p, r are array indices

17. Quicksort
p q r
… 1 2 6 … 22 9 5 …
}sub-array A[p…r]
p, r, q are array indices
7.1 Description of quicksort
Combine: Because the subarrays are already
them: the entire array AŒp : : r is now sort
The following procedure implements quicksor
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/

18. Quicksort — Partition
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the su
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
7.1 Description of quicksort
Combine: Because the subarrays are alr
them: the entire array AŒp : : r is no
The following procedure implements qu
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call
Partition is the central sorting
operation of quicksort
p q? r
… 1 2 6 … 22 9 5 …
}sub-array A[p…r]
p, r, q are array indices

19. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i p,j r,x
6 5 1 3 2 4

20. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i p,j r,x
6 5 1 3 2 4 pivot element

21. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
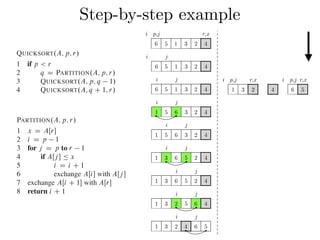
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4 x = 4, A[j = p+1] = 5 > x
i p,j r,x
6 5 1 3 2 4 pivot element

22. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
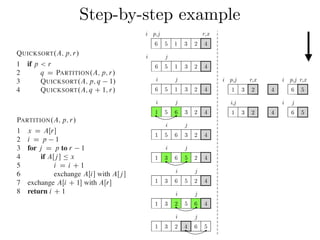
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
i p,j r,x
6 5 1 3 2 4 pivot element

23. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
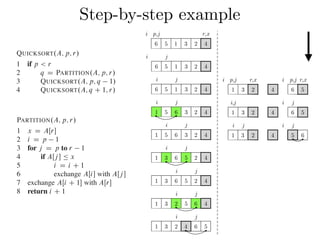
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
i p,j r,x
6 5 1 3 2 4 pivot element

24. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
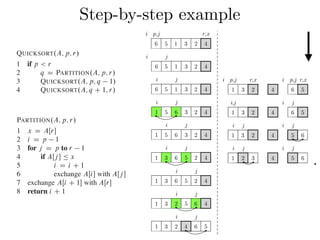
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
A[j = p+3] = 3 < x, i = i+1
i p,j r,x
6 5 1 3 2 4 pivot element

25. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
A[j = p+3] = 3 < x, i = i+1
and A[i]↔A[j]
i p,j r,x
6 5 1 3 2 4 pivot element

26. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
A[j = p+3] = 3 < x, i = i+1
and A[i]↔A[j]
i p,j r,x
6 5 1 3 2 4 pivot element

27. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
A[j = p+3] = 3 < x, i = i+1
and A[i]↔A[j]
i p,j r,x
6 5 1 3 2 4 pivot element

28. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
x = 4, A[j = p+1] = 5 > x
A[j = p+2] = 1 < x, i = i+1
and A[i]↔A[j]
A[j = p+3] = 3 < x, i = i+1
and A[i]↔A[j]
j = r−1, A[i+1]↔A[r]
i p,j r,x
6 5 1 3 2 4 pivot element

29. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i p,j r,x i p,j r,x
1 3 2 4 6 5
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5

30. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i,j i j
1 3 2 4 6 5
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
i p,j r,x i p,j r,x
1 3 2 4 6 5

31. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j i j
1 3 2 4 5 6
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
i,j i j
1 3 2 4 6 5
i p,j r,x i p,j r,x
1 3 2 4 6 5

32. Step-by-step exampleCombine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
always selects an element x D AŒr as a pivot element around which to partition the
subarray AŒp : : r. As the procedure runs, it partitions the array into four (possibly
empty) regions. At the start of each iteration of the for loop in lines 3–6, the regions
i j i j
1 2 3 4 5 6
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
i j i j
1 3 2 4 5 6
i,j i j
1 3 2 4 6 5
i p,j r,x i p,j r,x
1 3 2 4 6 5
.

33. Why does quicksort work?
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSO
Partitioning the array
The key to the algorithm is the PARTITION procedur
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
• As i goes through the array from left to
right, no element greater than the pivot
element (= 4) is left behind it. When such
element is identified, it is swapped.

34. Why does quicksort work?
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSO
Partitioning the array
The key to the algorithm is the PARTITION procedur
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
• As i goes through the array from left to
right, no element greater than the pivot
element (= 4) is left behind it. When such
element is identified, it is swapped.
• Elements i+1 to j−1 are always greater
than the pivot element.

35. Quicksort’s performance

36. • The performance is affected by the choice of the pivot element
during partitioning: balanced vs. unbalanced outcome
Quicksort’s performance

37. • The performance is affected by the choice of the pivot element
during partitioning: balanced vs. unbalanced outcome
• Worst case: Θ(n2)
— when partitioning is always completely unbalanced, i.e. the
choice of pivot generates sub-arrays that always have n−1
and 0 elements, respectively
— when the array is already sorted
Quicksort’s performance

38. • The performance is affected by the choice of the pivot element
during partitioning: balanced vs. unbalanced outcome
• Worst case: Θ(n2)
— when partitioning is always completely unbalanced, i.e. the
choice of pivot generates sub-arrays that always have n−1
and 0 elements, respectively
— when the array is already sorted
• Best case: Θ(n logn)
— when partitioning is always fairly balanced, i.e. the choice
of pivot generates sub-arrays that always have ⌊n/2⌋ and
⌈n/2⌉−1 elements, respectively
Quicksort’s performance

39. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6

40. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6

41. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6

42. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6

43. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6

44. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6

45. Step-by-step example for worst case
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i,j
1 2 3 4 5 6
i p,j r,x
1 2 3 4 5 6
i,j
1 2 3 4 5 6
1 2 3 4 5 6
.

46. Recall previous example (average case)
i j i j
1 2 3 4 5 6
i p,j r,x
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
6 5 1 3 2 4
i j
1 5 6 3 2 4
i j
1 5 6 3 2 4
i j
1 3 6 5 2 4
i j
1 3 6 5 2 4
i j
1 3 2 5 6 4
i j
1 3 2 4 6 5
i j i j
1 3 2 4 5 6
i,j i j
1 3 2 4 6 5
i p,j r,x i p,j r,x
1 3 2 4 6 5
.

47. Cost estimation (running time)To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges th
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PA
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. PARTITION
• Cost is mainly affected by the
partition operation, and
especially by the for-loop in it
that performs n−1 comparisons
• The cost for a single partition
operation is: Θ(n), where
n = r−p+1

48. Worst case cost estimation example (n = 8)
n = 8 n-dimensional array, cost: c ⁎ 8

49. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)

50. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60 cost: c ⁎ 7

51. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60
P 50
cost: c ⁎ 7
cost: c ⁎ 6

52. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60
P 50
P 40
cost: c ⁎ 7
cost: c ⁎ 6
cost: c ⁎ 5

53. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60
P 50
P 40
P 03
cost: c ⁎ 7
cost: c ⁎ 6
cost: c ⁎ 5
cost: c ⁎ 4

54. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60
P 50
P 40
P 03
cost: c ⁎ 7
cost: c ⁎ 6
cost: c ⁎ 5
P 02
cost: c ⁎ 4
cost: c ⁎ 3

55. Worst case cost estimation example (n = 8)
n = 8
n − 1 = 7 P 0
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ (7+1)
P 60
P 50
P 40
P 03
cost: c ⁎ 7
cost: c ⁎ 6
cost: c ⁎ 5
P 02
P 01
cost: c ⁎ 4
cost: c ⁎ 3
total cost: c ⁎ (8+8…+2) = c ⁎ 43 ≈ Θ(n2)
cost: c ⁎ 2

56. Worst case cost analysis (1/3)
• Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements

57. • Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements
• The cost of partitioning an array with n elements is Θ(n)
Worst case cost analysis (1/3)

58. • Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements
• The cost of partitioning an array with n elements is Θ(n)
T(n) = (T(q) + T(n − q − 1)) + Θ(n)So, the cost of quicksort is:
Worst case cost analysis (1/3)

59. T(n) = max
0≤q≤n−1
(T(q) + T(n − q − 1)) + Θ(n) (1)
• Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements
• The cost of partitioning an array with n elements is Θ(n)
In the worst case, this cost will be maximised, i.e.
T(n) = (T(q) + T(n − q − 1)) + Θ(n)So, the cost of quicksort is:
Worst case cost analysis (1/3)

60. T(n) = max
0≤q≤n−1
(T(q) + T(n − q − 1)) + Θ(n) (1)
T(n) = O(n2
) ≤ cn2
, where c > 0 (2)
• Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements
• The cost of partitioning an array with n elements is Θ(n)
In the worst case, this cost will be maximised, i.e.
Let’s now assume that:
T(n) = (T(q) + T(n − q − 1)) + Θ(n)So, the cost of quicksort is:
Worst case cost analysis (1/3)

61. T(n) = max
0≤q≤n−1
(T(q) + T(n − q − 1)) + Θ(n) (1)
T(n) = O(n2
) ≤ cn2
, where c > 0 (2)
• Performing partition once on an n-dimensional array, generates
2 sub-arrays with q and n−q−1 elements
• The cost of partitioning an array with n elements is Θ(n)
In the worst case, this cost will be maximised, i.e.
Let’s now assume that:
and substitute (1) in (2): T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
T(n) = (T(q) + T(n − q − 1)) + Θ(n)So, the cost of quicksort is:
Worst case cost analysis (1/3)

62. T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
= c max
0≤q≤n−1
(q2
+ (n − q − 1)2
) + Θ(n)
Worst case cost analysis (2/3)

63. T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
= c max
0≤q≤n−1
(q2
+ (n − q − 1)2
) + Θ(n)
g(q)
So, we want to maximise g(q) = q2
+ (n − q − 1)2
Worst case cost analysis (2/3)

64. T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
= c max
0≤q≤n−1
(q2
+ (n − q − 1)2
) + Θ(n)
g(q)
So, we want to maximise g(q) = q2
+ (n − q − 1)2
∂g
∂q
= 2q + 2(n − q − 1)(−1) = 4q − 2n + 2
∂g
∂q
= 0 ⟹ q =
1
2
(n − 1)
Worst case cost analysis (2/3)

65. T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
= c max
0≤q≤n−1
(q2
+ (n − q − 1)2
) + Θ(n)
g(q)
So, we want to maximise g(q) = q2
+ (n − q − 1)2
∂g
∂q
= 2q + 2(n − q − 1)(−1) = 4q − 2n + 2
∂g
∂q
= 0 ⟹ q =
1
2
(n − 1)
∂2
g
∂q2
= 4 > 0
Worst case cost analysis (2/3)

66. T(n) ≤ max
0≤q≤n−1
(cq2
+ c(n − q − 1)2
) + Θ(n)
= c max
0≤q≤n−1
(q2
+ (n − q − 1)2
) + Θ(n)
g(q)
So, we want to maximise g(q) = q2
+ (n − q − 1)2
∂g
∂q
= 2q + 2(n − q − 1)(−1) = 4q − 2n + 2
∂g
∂q
= 0 ⟹ q =
1
2
(n − 1)
∂2
g
∂q2
= 4 > 0
this is a local minimum of g(q)
Worst case cost analysis (2/3)

67. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for

68. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1

69. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2

70. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2
T(n) ≤ c(n − 1)2
+ Θ(n) = cn2
− 2cn + c + Θ(n) ≤ cn2

71. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2
T(n) ≤ c(n − 1)2
+ Θ(n) = cn2
− 2cn + c + Θ(n) ≤ cn2
which results in T(n) = O(n2
)

72. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2
T(n) ≤ c(n − 1)2
+ Θ(n) = cn2
− 2cn + c + Θ(n) ≤ cn2
which results in T(n) = O(n2
)
Also: T(n) ≥ c
1
2
(n − 1)2
+ Θ(n) =
cn2
2
+
c
2

73. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2
T(n) ≤ c(n − 1)2
+ Θ(n) = cn2
− 2cn + c + Θ(n) ≤ cn2
which results in T(n) = O(n2
)
Also: T(n) ≥ c
1
2
(n − 1)2
+ Θ(n) =
cn2
2
+
c
2
T(n) = Ω(n2
)which results in

74. Worst case cost analysis (3/3)
T(n) ≤ c max
0≤q≤n−1
g(q) + Θ(n) q =
1
2
(n − 1)g(q)min of for
max of g(q) for q = 0 or q = n − 1
g(0) = g(n − 1) = (n − 1)2
, g
(
n − 1
2 )
=
(n − 1)2
2
T(n) ≤ c(n − 1)2
+ Θ(n) = cn2
− 2cn + c + Θ(n) ≤ cn2
which results in T(n) = O(n2
)
Also: T(n) ≥ c
1
2
(n − 1)2
+ Θ(n) =
cn2
2
+
c
2
T(n) = Ω(n2
)which results in
Thus, T(n) = Θ(n2
) .

75. Best case cost estimation example (n = 8)
n = 8
n − 1 = 3 P 4
n-dimensional array, cost: c ⁎ 8
P: pivot element, cost: c ⁎ 7
P 11 P 12
P 01
cost: c ⁎ 5
cost: c ⁎ 2
total cost: c ⁎ (8+7+5+2) = c ⁎ 22 ≈ Θ(n logn)

76. Best case cost analysis
If the splits are even, partition produces two sub-problems,
each of which has no size more than n/2.

77. Best case cost analysis
If the splits are even, partition produces two sub-problems,
each of which has no size more than n/2.
Thus the running time is equal to:
T(n) = 2T(n/2) + Θ(n)

78. Best case cost analysis
If the splits are even, partition produces two sub-problems,
each of which has no size more than n/2.
Thus the running time is equal to:
T(n) = 2T(n/2) + Θ(n)
Using case 2 of the master theorem (see Theorem 4.1 in
Cormen et al. textbook, 3rd edition), this has the solution:
T(n) = Θ(n log n)
For T(n) = aT(n/b) + f(n),
if f(n) = Θ (nlogb a
), then T(n) = Θ (nlogb a
log n),
where b = 2 and a = 2.

79. • Instead of using the right-most element, A[r], as the pivot…
Randomised quicksort
element x D AŒr is equally likely to be any of the r p C 1 elements in the
subarray. Because we randomly choose the pivot element, we expect the split of
the input array to be reasonably well balanced on average.
The changes to PARTITION and QUICKSORT are small. In the new partition
procedure, we simply implement the swap before actually partitioning:
RANDOMIZED-PARTITION.A; p; r/
1 i D RANDOM.p; r/
2 exchange AŒr with AŒi
3 return PARTITION.A; p; r/
The new quicksort calls RANDOMIZED-PARTITION in place of PARTITION:
RANDOMIZED-QUICKSORT.A; p; r/
1 if p < r
2 q D RANDOMIZED-PARTITION.A; p; r/
3 RANDOMIZED-QUICKSORT.A; p; q 1/
4 RANDOMIZED-QUICKSORT.A; q C 1; r/
We analyze this algorithm in the next section.
subarray. Because we randomly choose the pivot element, we expect the split of
the input array to be reasonably well balanced on average.
The changes to PARTITION and QUICKSORT are small. In the new partition
procedure, we simply implement the swap before actually partitioning:
RANDOMIZED-PARTITION.A; p; r/
1 i D RANDOM.p; r/
2 exchange AŒr with AŒi
3 return PARTITION.A; p; r/
The new quicksort calls RANDOMIZED-PARTITION in place of PARTITION:
RANDOMIZED-QUICKSORT.A; p; r/
1 if p < r
2 q D RANDOMIZED-PARTITION.A; p; r/
3 RANDOMIZED-QUICKSORT.A; p; q 1/
4 RANDOMIZED-QUICKSORT.A; q C 1; r/
We analyze this algorithm in the next section.

80. • Instead of using the right-most element, A[r], as the pivot…
Randomised quicksort
element x D AŒr is equally likely to be any of the r p C 1 elements in the
subarray. Because we randomly choose the pivot element, we expect the split of
the input array to be reasonably well balanced on average.
The changes to PARTITION and QUICKSORT are small. In the new partition
procedure, we simply implement the swap before actually partitioning:
RANDOMIZED-PARTITION.A; p; r/
1 i D RANDOM.p; r/
2 exchange AŒr with AŒi
3 return PARTITION.A; p; r/
The new quicksort calls RANDOMIZED-PARTITION in place of PARTITION:
RANDOMIZED-QUICKSORT.A; p; r/
1 if p < r
2 q D RANDOMIZED-PARTITION.A; p; r/
3 RANDOMIZED-QUICKSORT.A; p; q 1/
4 RANDOMIZED-QUICKSORT.A; q C 1; r/
We analyze this algorithm in the next section.
subarray. Because we randomly choose the pivot element, we expect the split of
the input array to be reasonably well balanced on average.
The changes to PARTITION and QUICKSORT are small. In the new partition
procedure, we simply implement the swap before actually partitioning:
RANDOMIZED-PARTITION.A; p; r/
1 i D RANDOM.p; r/
2 exchange AŒr with AŒi
3 return PARTITION.A; p; r/
The new quicksort calls RANDOMIZED-PARTITION in place of PARTITION:
RANDOMIZED-QUICKSORT.A; p; r/
1 if p < r
2 q D RANDOMIZED-PARTITION.A; p; r/
3 RANDOMIZED-QUICKSORT.A; p; q 1/
4 RANDOMIZED-QUICKSORT.A; q C 1; r/
We analyze this algorithm in the next section.
• Why? By adding randomisation, obtaining the average expected
performance is more likely than obtaining the worst case
performance.

81. Average number of comparisons (1/3)
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.

82. Average number of comparisons (1/3)
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.
cn = 1 + (n − 1) + …

83. Average number of comparisons (1/3)
cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.

84. Average number of comparisons (1/3)
cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.
total number of
comparisons

85. Average number of comparisons (1/3)
cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.
total number of
comparisons
probability of a
split — n pivot
choices

86. Average number of comparisons (1/3)
cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
Combine: Because the subarrays are already sorted, no work is needed to combine
them: the entire array AŒp : : r is now sorted.
The following procedure implements quicksort:
QUICKSORT.A; p; r/
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges the subar-
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Partitioning the array
The key to the algorithm is the PARTITION procedure, w
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-e
always selects an element x D AŒr as a pivot element ar
subarray AŒp : : r. As the procedure runs, it partitions t
empty) regions. At the start of each iteration of the for lo
satisfy certain properties, shown in Figure 7.2. We stat
invariant:
At the beginning of each iteration of the loop of l
index k,
1. If p Ä k Ä i, then AŒk Ä x.
2. If i C 1 Ä k Ä j 1, then AŒk > x.
3. If k D r, then AŒk D x.
total number of
comparisons
probability of a
split — n pivot
choices
sub-array sizes

87. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
Average number of comparisons (2/3)

88. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
Average number of comparisons (2/3)

89. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
Average number of comparisons (2/3)
Replace n → n−1

90. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
Average number of comparisons (2/3)
subtract

91. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
ncn − (n − 1)cn−1 = 2(n − 1) + 2cn−1 ⟹
Average number of comparisons (2/3)
subtract

92. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
ncn − (n − 1)cn−1 = 2(n − 1) + 2cn−1 ⟹
Average number of comparisons (2/3)
subtract
cn =
2n − 1
n
+
(n + 1)cn−1
n
⟹

93. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
ncn − (n − 1)cn−1 = 2(n − 1) + 2cn−1 ⟹
Average number of comparisons (2/3)
subtract
cn =
2n − 1
n
+
(n + 1)cn−1
n
⟹ divide by n + 1

94. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
ncn − (n − 1)cn−1 = 2(n − 1) + 2cn−1 ⟹
cn
n + 1
=
2
n + 1
−
1
n(n + 1)
+
cn−1
n
Average number of comparisons (2/3)
subtract
cn =
2n − 1
n
+
(n + 1)cn−1
n
⟹ divide by n + 1

95. cn = n +
1
n [(c0 + cn−1) + (c1 + cn−2) + … + (cn−1 + c0)]
= n +
2
n
(c0 + c1 + … + cn−1) ⟹
ncn = n2
+ 2 (c0 + c1 + … + cn−1)
(n − 1)cn−1 = (n − 1)2
+ 2 (c0 + c1 + … + cn−2)
ncn − (n − 1)cn−1 = 2(n − 1) + 2cn−1 ⟹
cn
n + 1
=
2
n + 1
−
1
n(n + 1)
+
cn−1
n
Average number of comparisons (2/3)
subtract
cn =
2n − 1
n
+
(n + 1)cn−1
n
⟹ divide by n + 1
≤
2
n + 1
+
cn−1
n

96. Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1

97. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1

98. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
= … =
c1
2
+ 2
(
1
n + 1
+
1
n
+ … +
1
3)
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1

99. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
= … =
c1
2
+ 2
(
1
n + 1
+
1
n
+ … +
1
3)
=
c1
2
+ 2
n
∑
i=2
1
i + 1
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1

100. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
= … =
c1
2
+ 2
(
1
n + 1
+
1
n
+ … +
1
3)
=
c1
2
+ 2
n
∑
i=2
1
i + 1
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1
≤ 2
n
∑
i=1
1
i

101. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
= … =
c1
2
+ 2
(
1
n + 1
+
1
n
+ … +
1
3)
=
c1
2
+ 2
n
∑
i=2
1
i + 1
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1
≤ 2
n
∑
i=1
1
i
= 2Hn ≈ 2 loge(n) ⟹
Harmonic series
or ln(n)

102. =
cn−2
n − 1
+
2
n
+
2
n + 1
=
cn−3
n − 2
+
2
n − 1
+
2
n
+
2
n + 1
= … =
c1
2
+ 2
(
1
n + 1
+
1
n
+ … +
1
3)
=
c1
2
+ 2
n
∑
i=2
1
i + 1
cn ≤ 2(n + 1)loge(n) = 2(n + 1)
log2 n
log2 e
≈ 1.39(n log2 n + log2 n) = O(n log n) .
Average number of comparisons (3/3)
cn
n + 1
≤
cn−1
n
+
2
n + 1
replace n → n−1
≤ 2
n
∑
i=1
1
i
= 2Hn ≈ 2 loge(n) ⟹
Harmonic series
change of base
or ln(n)

103. Average number of comparisons, take II (1/4)
• At most n calls to partition over the execution of quicksort
because every time partition is called, it will handle at least
one element
• Every call to the partition takes O(1) + lines 3-6 (focus on
the number of comparisons)
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. P
always selects an element x D AŒr as a pivot element around which to p
subarray AŒp : : r. As the procedure runs, it partitions the array into fou
empty) regions. At the start of each iteration of the for loop in lines 3–6, t
satisfy certain properties, shown in Figure 7.2. We state these propertie

104. Average number of comparisons, take II (1/4)
• At most n calls to partition over the execution of quicksort
because every time partition is called, it will handle at least
one element
• Every call to the partition takes O(1) + lines 3-6 (focus on
the number of comparisons)
1 if p < r
2 q D PARTITION.A; p; r/
3 QUICKSORT.A; p; q 1/
4 QUICKSORT.A; q C 1; r/
To sort an entire array A, the initial call is QUICKSORT.A; 1; A:length/.
Partitioning the array
The key to the algorithm is the PARTITION procedure, which rearranges
ray AŒp : : r in place.
PARTITION.A; p; r/
1 x D AŒr
2 i D p 1
3 for j D p to r 1
4 if AŒj  Ä x
5 i D i C 1
6 exchange AŒi with AŒj 
7 exchange AŒi C 1 with AŒr
8 return i C 1
Figure 7.1 shows how PARTITION works on an 8-element array. P
always selects an element x D AŒr as a pivot element around which to p
subarray AŒp : : r. As the procedure runs, it partitions the array into fou
empty) regions. At the start of each iteration of the for loop in lines 3–6, t
satisfy certain properties, shown in Figure 7.2. We state these propertie
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!

105. Average number of comparisons, take II (2/4)
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!
Notation
• A is a set containing elements {z1,z2,…,zn}, where zi is the i-th
smallest element — A’s are not presumed to be sorted

106. Average number of comparisons, take II (2/4)
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!
Notation
• A is a set containing elements {z1,z2,…,zn}, where zi is the i-th
smallest element — A’s are not presumed to be sorted
• Zij = {zi,zi+1,…,zj} is a set that contains elements from zi to zj

107. Average number of comparisons, take II (2/4)
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!
Notation
• A is a set containing elements {z1,z2,…,zn}, where zi is the i-th
smallest element — A’s are not presumed to be sorted
• Zij = {zi,zi+1,…,zj} is a set that contains elements from zi to zj
How many times does quicksort compare elements zi and zj?

108. Average number of comparisons, take II (2/4)
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!
Notation
• A is a set containing elements {z1,z2,…,zn}, where zi is the i-th
smallest element — A’s are not presumed to be sorted
• Zij = {zi,zi+1,…,zj} is a set that contains elements from zi to zj
How many times does quicksort compare elements zi and zj?
• Any pair of elements of A is compared at most once… because
elements are only compared to the pivot element.
• Reminder: Once used, the pivot element is not used again.

109. Average number of comparisons, take II (2/4)
If the entire quicksort requires m comparisons, then its running
time is O(n+m). Let’s estimate m!
Notation
• A is a set containing elements {z1,z2,…,zn}, where zi is the i-th
smallest element — A’s are not presumed to be sorted
• Zij = {zi,zi+1,…,zj} is a set that contains elements from zi to zj
How many times does quicksort compare elements zi and zj?
• Any pair of elements of A is compared at most once… because
elements are only compared to the pivot element.
• Reminder: Once used, the pivot element is not used again.
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.

110. Average number of comparisons, take II (3/4)
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.
Total number of comparisons: m =
n−1
∑
i=1
n
∑
j=i+1
mij

111. Average number of comparisons, take II (3/4)
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.
Total number of comparisons: m =
n−1
∑
i=1
n
∑
j=i+1
mij
E(m) = E
n−1
∑
i=1
n
∑
j=i+1
mij =
n−1
∑
i=1
n
∑
j=i+1
E (mij) what is m’s expectation?

112. Average number of comparisons, take II (3/4)
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.
Total number of comparisons: m =
n−1
∑
i=1
n
∑
j=i+1
mij
E(m) = E
n−1
∑
i=1
n
∑
j=i+1
mij =
n−1
∑
i=1
n
∑
j=i+1
E (mij) what is m’s expectation?
=
n−1
∑
i=1
n
∑
j=i+1
Pr{zi is compared to zj}

113. Average number of comparisons, take II (3/4)
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.
Total number of comparisons: m =
n−1
∑
i=1
n
∑
j=i+1
mij
E(m) = E
n−1
∑
i=1
n
∑
j=i+1
mij =
n−1
∑
i=1
n
∑
j=i+1
E (mij) what is m’s expectation?
=
n−1
∑
i=1
n
∑
j=i+1
Pr{zi is compared to zj}
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?

114. Average number of comparisons, take II (3/4)
Hence, mij = 1, if zi is compared to zj, and 0 otherwise.
Total number of comparisons: m =
n−1
∑
i=1
n
∑
j=i+1
mij
E(m) = E
n−1
∑
i=1
n
∑
j=i+1
mij =
n−1
∑
i=1
n
∑
j=i+1
E (mij) what is m’s expectation?
=
n−1
∑
i=1
n
∑
j=i+1
Pr{zi is compared to zj}
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.

115. Average number of comparisons, take II (4/4)
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.

116. Average number of comparisons, take II (4/4)
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.
• Zij has j−i+1 elements. Selecting one of them as the first pivot
has a probability of 1/(j−i+1).

117. Average number of comparisons, take II (4/4)
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.
• Zij has j−i+1 elements. Selecting one of them as the first pivot
has a probability of 1/(j−i+1).
Pr{zi is compared to zj} = Pr{zi or zj are the first pivots} =
2
j − i + 1

118. Average number of comparisons, take II (4/4)
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.
• Zij has j−i+1 elements. Selecting one of them as the first pivot
has a probability of 1/(j−i+1).
Pr{zi is compared to zj} = Pr{zi or zj are the first pivots} =
2
j − i + 1
E(m) =
n−1
∑
i=1
n
∑
j=i+1
Pr{zi is compared to zj} =
n−1
∑
i=1
n
∑
j=i+1
2
j − i + 1

119. Average number of comparisons, take II (4/4)
• Note that when the pivot element x is zi < x < zj, zi and zj are
not going to be compared. Why?
• To compare them we need to select zi or zj as pivots.
• Zij has j−i+1 elements. Selecting one of them as the first pivot
has a probability of 1/(j−i+1).
Pr{zi is compared to zj} = Pr{zi or zj are the first pivots} =
2
j − i + 1
E(m) =
n−1
∑
i=1
n
∑
j=i+1
Pr{zi is compared to zj} =
n−1
∑
i=1
n
∑
j=i+1
2
j − i + 1
k = j − i, then E(m) =
n−1
∑
i=1
n
∑
k=1
2
k + 1
<
n−1
∑
i=1
n
∑
k=1
2
k
≈
n−1
∑
i=1
O (log n) = O (n log n) .
Similar to the
previous proof

120. end_of_lecture
@lampos
lampos.net www
Slides (with potential revisions)
lampos.net/slides/quicksort2019.pdf