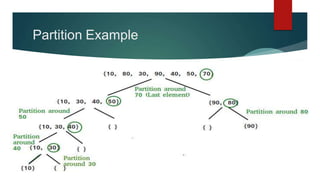
The document provides an overview of the quicksort sorting algorithm, detailing its method of arranging elements in ascending or descending order. It outlines the choice of pivot for partitioning the array and includes pseudocode and a C++ implementation of the algorithm. Quicksort's complexities indicate that it averages O(n log n) efficiency, with a worst-case scenario of O(n²), though the latter can typically be avoided.

1. Quicksort
MADE BY
SANIA NISAR

2. INTRODUCTIO
N
What is sorting?
Sorting breaks large data into smaller data units.
What is quicksort?
Arranges the element of array systematically or orderly.
The order could be ascending (moving from less to greater) or
descending (moving from greater to less).
Quicksort (sometimes called partition-exchange sort) is an efficient
sorting algorithm.

3. Quicksort Method

4. Choice of Pivot
Determine the pivot :
Many different approaches
The first element of the current sub-array
The last element
The middle element
The median of first , middle and last elements
Randomly choose an element

5. Quicksort Algorithm
Using pivot algorithm recursively, we end up with smaller possible partitions. Each partition is
then processed for quick sort. We define recursive algorithm for quicksort as follows −
Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value Step
3 − quicksort left partition recursively Step 4 −
quicksort right partition recursively

6. Partition
Code

7. Partition Example

8. Quicksort Pseudocode
 Procedure quicksort(Left ,
Right)
 if right-left <= 0
 retur
n
 else
 pivot = A[right]
 partition = partitionFunc(left, right, pivot)


quickSort(left,partition-1)
quickSort(partition+1,right)
 end if
 end procedure

9. Quicksort Implementation
#include < iostream >
using namespace std ;
void quick_sort (int[],int,int); int
partition (int[],int,int);
int main()
{
int a[50],n,i;
cout<<"How many elements?";
cin>>n;
cout<<"n Enter array elements:";
for(i=0;i<n;i++)
cin>>a[i];

10. quick_sort (a,0,n-1);
cout<<"n Array after sorting:";
for(i=0;i<n;i++)
cout<<a[i]<<" ";
return 0;
}
void quick_sort (int a[],int l,int u)
{
int j;
if(l<u)
{
j=partition(a,l,u);
quick_sort(a,l,j-1);
quick_sort(a,j+1,u);
}
}

11. int partition (int a[],int l,int u)
{
int v,i,j,temp;
v=a[l];
i=l;
j=u+1;
do
{
do
i++;
while(a[i]<v&&i<=u);
do
j--;
while(v<a[j]);
if(i<j)
{
temp=a[i];
a[i]=a[j];
a[j]=temp;
}

12. }
while(i<j);
a[l]=a[j];
a[j]=v;
return(j);
}
Output
How many elements?
6
Enter array elements:
9 15 6 7 10 12
Array after
sorting: 6 7 9 10
12 15

13. Quicksort Complexities

14. Quicksort Uses

15. REVIE
W
What will be the worst case for the algorithm?
Partition is always unbalanced
 What will be the best case for the algorithm?
Partition is balanced

16. SUMMAR
Y
 In worst case efficiency is O(n2)
---But easy to avoid the worst case
 On average efficiency is O(n log n)
 Better space complexity than merge sort
 In practice , runs fast and widely used

17. EN
D