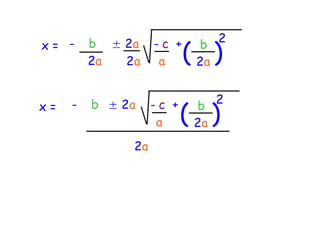
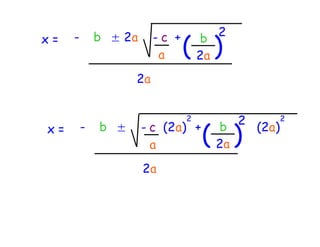
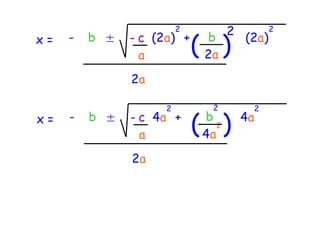
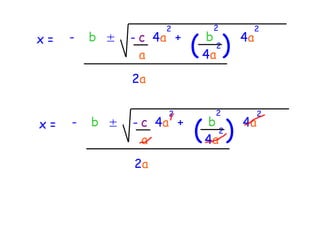
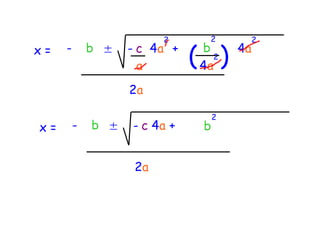
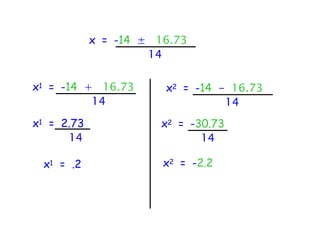
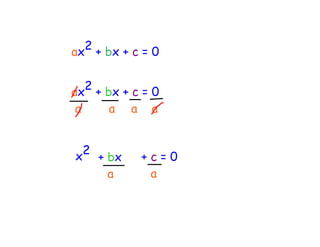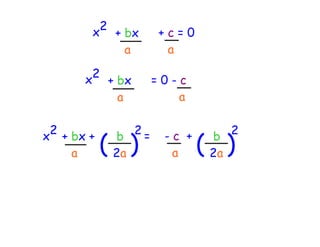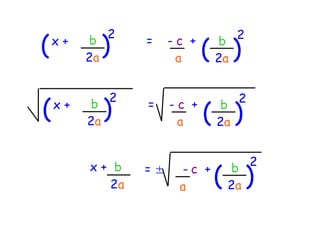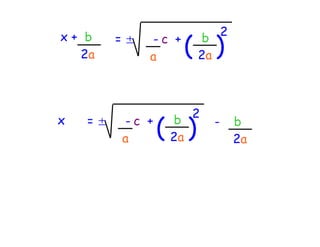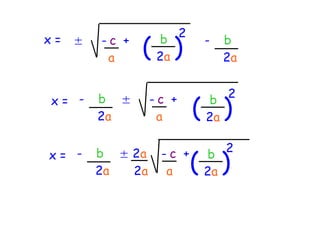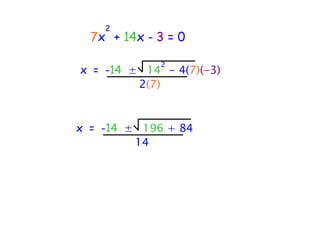The quadratic formula provides a method to solve quadratic equations of the form ax^2 + bx + c = 0. It expresses the solutions for x in terms of the coefficients a, b, and c as x = (-b ± √(b^2 - 4ac))/2a. The document demonstrates applying the quadratic formula to solve the equation 7x^2 + 14x - 3 = 0, obtaining the two solutions x1 = 0.2 and x2 = -2.2.

1. Quadratic Formula

2. Quadratics come in this form:
ax 2 + bx + c = 0
Sometimes it is factorable and finding
the value(s) of x is easy. What do you do
when it isn't factorable?
Can you still solve for x?

3. 2 + bx + c = 0
ax
2 + bx + c = 0
ax
a a a a
2
x + bx +c=0
a a

4. x 2
+ bx +c=0
a a
x 2
+ bx =0-c
a a
2 2= 2
x + bx +
a ( )
b
2a
-c +
a ( )
b
2a

5. 2 2
( x+ b
2a
) = -c +
a ( )
b
2a
2 2
( x+ b
2a
) = -c +
a ( )
b
2a
2
( )
x+ b =± -c + b
2a a 2a

6. 2
( )
x+ b =± -c + b
2a a 2a
2
x =± -c +
a
( )
b
2a
- b
2a

7. 2
x= ± -c +
a
( )b
2a
- b
2a
2
x= -
( )
b ± -c + b
2a a 2a
2
x= -
( )
b ± 2a -c + b
2a 2a a 2a

8. 2
x= -
( )
b ± 2a -c + b
2a 2a a 2a
2
( )
x= - b ± 2a -c + b
a 2a
2a

9. 2
( )
x= - b ± 2a -c + b
a 2a
2a
2 2 2
x= - b ± - c (2a) +
a ( )
b
2a
(2a)
2a

10. 2 2 2
x= - b ± - c (2a) +
a ( )
b
2a
(2a)
2a
2 2 2
x= - b ± - c 4a +
a
( )
b
4a
2
4a
2a

11. 2 2 2
x= - b ± - c 4a +
a ( )
b
4a
2
4a
2a
2 2 2
x= - b ± - c 4a +
a ( )
b
4a
2
4a
2a

12. 2 2 2
x= - b ± - c 4a +
a ( )
b
4a
2
4a
2a
2
x= - b ± - c 4a + b
2a

13. 2
x = -b ± b - 4ac
2a

14. 2
7x + 14x - 3 = 0
What are the roots of
the above function
2
x = -b ± b - 4ac
2a
2
7x + 14x - 3 = 0

15. 2
7x + 14x - 3 = 0
2
x = -14 ± 14 - 4(7)(-3)
2(7)
x = -14 ± 196 + 84
14

16. x = -14 ± 280
14
x = -14 ± 16.73
14

17. x = -14 ± 16.73
14
x1 = -14 + 16.73 x2 = -14 - 16.73
14 14
x1 = 2.73 x2 = -30.73
14 14
x1 = .2 x2 = -2.2