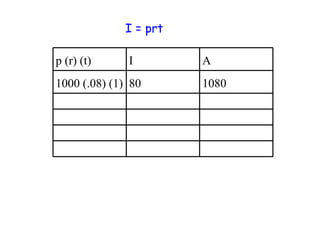
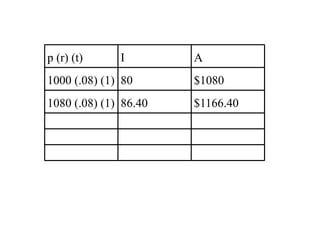
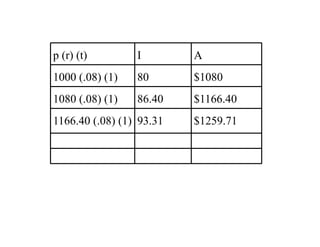
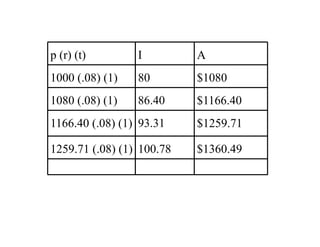
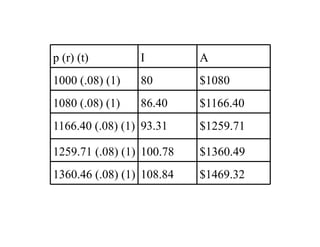
The document explains compound interest using examples of borrowing $1000 at 8% interest for 1 year, and then not paying it back for additional years. It shows how the interest builds on itself each year, with the borrower paying interest on accumulated interest. A formula is provided to calculate the final amount for any principal, interest rate, number of compounding periods per year, and term of years. An example calculates the amount owed after 2 years at 6% interest compounded semi-annually.

1. Compound Interest

2. Example
Calculate the interest and the
final amount if $1000 is
borrowed for 1 year at 8%.

3. I = prt
p (r) (t) I A
1000 (.08) (1) 80 1080

4. What if the person did not pay back
the loan? What would be the new
amount owing if he didn't pay it back
for another year?

5. p (r) (t) I A
1000 (.08) (1) 80 $1080
1080 (.08) (1) 86.40 $1166.40

6. What if he still didn't pay it
back for another year?

7. p (r) (t) I A
1000 (.08) (1) 80 $1080
1080 (.08) (1) 86.40 $1166.40
1166.40 (.08) (1) 93.31 $1259.71

8. What about another year?

9. p (r) (t) I A
1000 (.08) (1) 80 $1080
1080 (.08) (1) 86.40 $1166.40
1166.40 (.08) (1) 93.31 $1259.71
1259.71 (.08) (1) 100.78 $1360.49

10. Another?

11. p (r) (t) I A
1000 (.08) (1) 80 $1080
1080 (.08) (1) 86.40 $1166.40
1166.40 (.08) (1) 93.31 $1259.71
1259.71 (.08) (1) 100.78 $1360.49
1360.46 (.08) (1) 108.84 $1469.32

12. This is called compound
interest. The interest builds
on itself. You pay interest on
the interest.

13. There is a formula to answer the
example more quickly.
A = p (1 + r/n) nt
A = the final amount (principal plus interest)
p = the principal
r = rate in decimal form
n = the number of times interest will be paid
in a year
t = time in years

14. Example
A = p (1 + r/n) nt
p = 1000
r = .08
t =5
n=1
(1)(5)
A = 1000(1 + .08/1)
A = $1469.32

15. example 2
How much is owed if $1000 is borrowed
for 2 year at 6% compounded semi-
annually.
p = 1000
r = .06
t=2
n=2
A = 1000(1 + .06/2) 2(2)
A = $1125.51

16. Daily = once a day = 365 times per year
Weekly = once a week = 52 times per year
Monthly = once a month = 12 times per year
Annually = once a year = 1 times per year
Semi-annually = every 6 months = 2 times per
year
Quarterly = every 3 months = 4 times per year