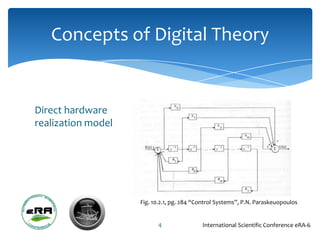
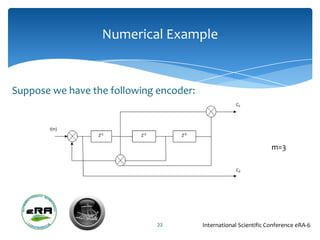
1) The document discusses state equations that can model digital control systems based on modulo-2 arithmetic and their application to recursive convolutional coding. 2) State equations can be derived from the transfer function of a discrete-time controller and expressed using modulo-2 arithmetic. 3) A recursive convolutional encoder can be modeled by state equations in modulo-2 algebra, where the state at each time step is a function of the previous states and the input bit.

1. State equations model based on
modulo-2 arithmetic and its
application on recursive
convolutional coding
Ch. N. Tasiopoulos, A.A. Fotopoulos, K.P. Peppas,
P.H. Yannakopoulos
International Scientific Conference eRA-6

2. Introduction
According to the theory of control systems, a time-
invariant system can be represented by a block diagram
with feedback for error correction, such a system can
be modeled by state equations. These equations can be
derived from the transfer function of the given system,
expressed in zeta transformation.
2 International Scientific Conference eRA-6

3. Concepts of Digital Theory
A discrete time controller can be described from the
transfer function:
1
U ( z) b( z ) b0 b1 z b2 z 2  bn z n
Gc ( z ) 1
E( z) a( z ) a0 a1 z a2 z 2  an z n
3 International Scientific Conference eRA-6

4. Concepts of Digital Theory
Direct hardware
realization model
Fig. 10.2.1, pg. 284 “Control Systems”, P.N. Paraskeuopoulos
4 International Scientific Conference eRA-6

5. Concepts of Digital Control Theory
State Equations
x(k+1)= Ax(k)+be(k) where:
u(k) = cTx(k)+de(k) 0 1 0 ... 0 0 bn anb0
0 0 1 ... 0 0 bn 1 an 1b0
A=      , b=  , c= 
0 0 0  1 0 b2 a2 b0
an an 1 an 2  a1 1 b1 a1b0
and the Constant d=b0
5 International Scientific Conference eRA-6

6. Concepts of Information
& Control Theory
Group definition
A group (G,*) is a pair consisting of a set G and an operation
* on that set , that is a function from the Cartesian product
GxG to G , with the result of operating on a and b denoted
by a*b , which satisfies
1. Associativity : a*(b*c)= (a*b)*c for all a, b, c G
2. Existence of identity: There exists e G such that
e*a=a and a*e=a for all a G
1
3.Existence of inverses: For each a G there exists a G
such that a * a 1 =e and a 1 * a =e
6 International Scientific Conference eRA-6

7. Concepts of Information
& Control Theory
Cyclic Groups definition
For each positive integer p, there is a group called the cyclic
group of order p, with set of elements
Zp {0,1,,( p 1)}
and operation defined by i j i j
If i j p , where (+ )denotes the usual operation
of addition of integers, and i j i j p
If i j p ,where (-) denotes the usual operation of subtraction of integers.
The operation in the cyclic group is addition modulo p. We shall use the sign +
instead of to denote this operation in what follows and refer to “the cyclic
Group ( Z p , ) ” , or simply the cyclic group Z
p
7 International Scientific Conference eRA-6

8. Concepts of Information
& Control Theory
Ring definition
A ring is a triple ( R, , ) consisting of a set R, and two operations + and , referred
to as addition and multiplication, respectively, which satisfy the following conditions:
1.Associativity of +: a (b c) (a b) c, for all a,b,c R
2.Commutativity of +: a b b a for all a,b R
3.Existence of additive identity: there exists 0 R such that 0 a a and a 0 a for all a R
a ( a) 0
4.Existence of additive inverses: for each a R there exists a R such that and ( a) a 0
5.Associativity of : a (b c) (a b) c, for all a, b, c R
6. Distributivity of over +: a (b c) (a b)(a c), for all a, b, c R
8 International Scientific Conference eRA-6

9. Concepts of Information
& Control Theory
Cyclic Groups definition
For every positive integer p, there is a ring (Z p , , ) , called the cyclic ring of order p,
with set of elements
Zp {0,1,,( p 1)}
and operations + denoting addition modulo p, and denoting multiplication modulo p
9 International Scientific Conference eRA-6

10. Modulo-2 Arithmetic
From the cyclic groups definition we have: Zp {0,1,,( p 1)}
The equation becomes for p=2: Z2 {0,1}
Where Z 2 is a cyclic group in modulo-2 arithmetic.
The operations stands as referred previously.
10 International Scientific Conference eRA-6

11. State equations & modulo-2
Assume the following transfer function:
1
U ( z) b( z ) b0 b1 z b2 z 2  bn z n
Gc ( z ) 1
E( z) a( z ) a0 a1 z a2 z 2  an z n
with b0b1b2bn GF (2) and a0 a1a2an GF (2)
The differential equation will be:
1 2
U ( z)(a0 a1z a2 z ... an z n ) e( z)(b0 b1z 1
b2 z 2
... bn z n )
11 International Scientific Conference eRA-6

12. State equations & modulo-2
1 2 n 1 2 n
u( z)a0 u( z)a1z u( z)a2 z ... u(z)an z e(z )b0 e(z )b1z e(z )b2 z ... e(z )bn z
Applying inverse Z transform with k 0,1, 2,...m GF (10)
we have:
u(k )a0 u(k 1)a1 u(k 2)a2 ... u(k n)an e(k )b0 e(k 1)b1 e(k 2)b2 ... e(k n)bn
12 International Scientific Conference eRA-6

13. State equations & modulo-2
The above differential
equation has the
following
direct hardware
realization:
Fig. 10.2.1, pg. 284 “Control Systems”, P.N. Paraskeuopoulos
13 International Scientific Conference eRA-6

14. State equations & modulo-2
Based on the above figure we derive the following
recursive signal equations:
xn ( k 1) e( n ) a1 xn ( k ) a2 xn 1 (k ) ... an x1 (k )
xn ( k ) xn 1 (k 1)
xn 1 (k ) xn 2 (k 1)

x2 ( k ) x1 ( k 1)
x1 ( k )
14 International Scientific Conference eRA-6

15. State equations & modulo-2
0 1 0 ... 0 0 bn anb0
x( k 1) Ax ( k ) be( k ) 0 0 1 ... 0 0 bn 1 an 1b0
A=      , b=  , c= 
u (k ) cT x( k ) de( k ) 0 0 0  1 0 b2 a2 b0
an an 1 an 2  a1 1 b1 a1b0
where: , b, c, d GF (2)
15 International Scientific Conference eRA-6

16. Implementation in recursive
convolutional coding
16 International Scientific Conference eRA-6

17. Description of Recursive
Convolutional Encoder
17 International Scientific Conference eRA-6

18. Description of Recursive
Convolutional Encoder
o The convolutionally encoding data, requires the use of n memory
registers, each holding 1 input bit, unless otherwise specified. All
memory registers start with a value of zero (0).
o The encoder has n modulo-2 adders and n generator polynomials
o Using the generator polynomials and the existing values in the
remaining registers, the encoder outputs n bits.
o I(n) consists the Input data and C1,C2,Cn the output data
18 International Scientific Conference eRA-6

19. Recursive Convolutional Encoder
Based on the figure we derive
the following recursive signal
equations:
X1 n = X1 n
X1 n-1 = X 2 n
X 2 n-1 = X 3 n = X1 n-2
X 3 n-1 =X 4 n =X1 n-3

X n-1 n-1 =X n n
Xn n-1
19 International Scientific Conference eRA-6

20. Algebraic Form of State Equations of
Recursive Convolutional Encoder in modulo-2
From the recursive signal equations
we have the algebraic form of state
equations: m
xm (n 1) xi (n) I (n) where m is the number of registers
i 1
m
cj xi (n) dI (n) where 1 j n
i 1
n, m, i, j GF (10)
with:
X , I , c, d GF (2)
20 International Scientific Conference eRA-6

21. Vector Form of State Equations of Recursive
Convolutional Encoder in modulo-2
From the recursive signal equations
we have the vector form of state
equations:
0 1 0 ... 0 0 bn anb0
X (n 1) AX (n) bI (n) 0 0 1 ... 0 0 bn 1 an 1b0
A=      , b=  , c= 
Cj cT X (n) dI (n) 0 0 0  1 0 b2 a2 b0
an an 1 an 2  a1 1 b1 a1b0
n, j, e GF (10)
with:
A, b, c, d , I , a, b GF (2)
21 International Scientific Conference eRA-6

22. Numerical Example
Suppose we have the following encoder:
m=3
22 International Scientific Conference eRA-6

23. Numerical Example
By applying the recursive signal formula for this particular model
we have:
X1(n)=X1(n)
X1(n-1)=X2(n)
X2(n-1)=X3(n)
X3(n-1)=X1(n)-I(n)-X3(n)-X2(n)
23 International Scientific Conference eRA-6

24. Numerical Example
Using these equations we can derive the state equations:
x1( n 1)
0 1 0 x1( n ) 0
x2( n 2) = 0 0 1 x2( n ) + 0 I(n)
x3( n 3)
1 1 1 x3( n ) 1
24 International Scientific Conference eRA-6

25. Numerical Example
Now we will study the controllability & observability of the given
system:
The determinant of s is given by the
s B  AB  A2 B following formula:
0 0 0 1 0 1 0 1
1 3 3
AB 1 s 0 1 1 det( s) 0 0 ( 1) det( s) 1
1 1 1 1
1 1 1 0
1 det(s) 1 0 1 1 0
2
AB 1
0 The system is controllable
25 International Scientific Conference eRA-6

26. Numerical Example
For finding if the system is observable we have:
C1 1 0 1 C2 1 0 0
R1 C1 A det( R) 1 0 1 det( R) 0 R2 C2 A det( R ) 0 1 0 1 0
C1 A2 1 1 1 C2 A 2 0 0 1
The system is observable only for the C2 output
26 International Scientific Conference eRA-6

27. Thank you for your attention
Evariste Galois
1811-1832
27 International Scientific Conference eRA-6