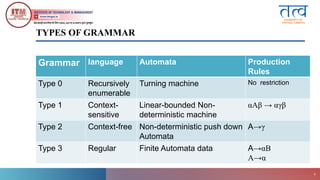
The document discusses types of grammars in the context of computation, as defined by Noam Chomsky's model. It categorizes grammars into four types based on production rules and derives specific languages recognized by different automata. Additionally, it highlights the applications of grammar in programming languages, compilers, and parsing.

1. ITM
Gwalior
1
INSTITUTE OF TECHNOLOGY AND MANAGEMENT
TOPIC: TYPES OF GRAMMAR
CS-501(A):Theory of computation
Presented to- Presented by-
Dr . Deepak Gupta Abhay Dhupar 0905CS191001
Associate Professor Abhay Singh 0905CS191002
(Dept. of CSE) Abhinav Goyal 0905CS191003
Abhinav Gupta 0905CS191004

2. GRAMMARS
• Noam Chomsky gave a mathematical model of grammar.
This model is used to write computer languages effectively.
• Grammar in theory of computation is a finite set of formal
rules that are generating syntactically correct sentences.
• The formal definition of grammar is that it is defined as four
tuples
ITM
Gwalior
2

3. CONT.
 G=(V,T,P,S)
 G is a grammar, which consists of a set of production rules. It is used to generate
the strings of a language.
 T is the final set of terminal symbols. It is denoted by lower case letters.
 V is the final set of non-terminal symbols. It is denoted by capital letters.
 P is a set of production rules, which is used for replacing non-terminal symbols
(on the left side of production) in a string with other terminals (on the right side
of production).
 S is the start symbol used to derive the string.
ITM
Gwalior
3

4. CONT.
• V = { S , A , B } => Non-Terminal symbols
• T = { a , b } => Terminal symbols
• P = { S → ABa , A → Ba , B → ab} => Production rules
• S = { S } => Start symbol
ITM
Gwalior
4

5. ITM
Gwalior
5

6. ITM
Gwalior
6

7. DIFFERENT TYPES OF GRAMMAR
Grammar can be divided on basis of –
 Type of Production Rules
 Number of Derivation Trees
 Number of Strings
ITM
Gwalior
7

8. CONT.
ITM
Gwalior
8

9. TYPES OF GRAMMAR
Grammar language Automata Production
Rules
Type 0 Recursively
enumerable
Turning machine No restriction
Type 1 Context-
sensitive
Linear-bounded Non-
deterministic machine
αAβ → αγβ
Type 2 Context-free Non-deterministic push down
Automata
A→γ
Type 3 Regular Finite Automata data A→αB
A→α
ITM
Gwalior
9

10. CONT.
ITM
Gwalior
10

11. TYPE 0
ITM
Gwalior
11
Type 0 grammar language are recognized by turing machine.
Grammar Production in the form of
where
α is ( V + T)* V ( V + T)*
β is ( V + T )*.
In type 0 there must be at least one variable on Left side of production.
Ex -
Sab –> ba
A –> S.

12. TYPE 1
Type-1 grammars generate the context-sensitive languages.
The language generated by the grammar are recognized by the Linear
Bound Automata
In Type 1,
I. First of all Type 1 grammar should be Type 0.
II. Grammar Production in the form of
|α | <= | β |
i.e count of symbol in α is less than or equal to
Ex S –> AB
AB –> abc
B –> b
ITM
Gwalior
12

13. TYPE 2
Type-2 grammars generate the context-free languages. The language
generated by the grammar is recognized by a Pushdown automata.
In Type 2,
1. First of all it should be Type 1.
2. Left hand side of production can have only one variable.
|α| = 1.
Their is no restriction on β .
Ex -
S –> AB
A –> a
B –> b
ITM
Gwalior
13

14. TYPE 3
Type-3 grammars generate regular languages. These languages are
exactly all languages that can be accepted by a finite state automaton.
Type 3 is most restricted form of grammar.
It should be in the given form only :
V –> VT / T (left-regular grammar)
(or)
V –> TV /T (right-regular grammar)
Ex -
S –> a
ITM
Gwalior
14

15. APPLICATION OF GRAMMAR
• For defining programming languages
• For parsing the program by constructing syntax tree
• For translation of programming languages
• For describing arithmetic expressions
• For construction of compilers, etc.
ITM
Gwalior
15

16. THANK YOU
ITM
Gwalior
16