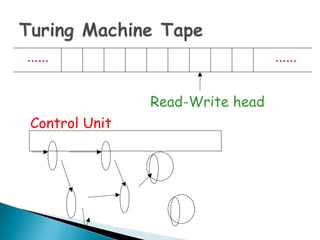
A Turing machine consists of a finite-state control unit, an infinite tape divided into cells to hold symbols, and a read/write head. At each step, the control unit reads the symbol under the head, writes a symbol, and moves the head left or right. It can enter a new state depending on the symbol and its current state. Turing machines can recognize, generate, evaluate, and decide languages by looping through state transitions and tape operations until reaching an accepting or rejecting state. They provide a model for general computation that is theoretically more powerful than finite state machines.

2.  Conceptually a Turing machine, like finite
automata
 A Turing machine consists of a finite-state control
unit and a tape that is infinite in both directions and
divided into cells, each of which can hold one symbol:
 At each step, the control unit performs two actions
in a way dependent on:
 The two actions will be:
 1. either
 – move the read/write head one cell to the left or
right;
 2. put the control unit into a new state

3. Turing machine will be your ultimate
model for computer.
In Turing machine output is very
important.
We know that every program has an
output but this is not exactly true.

4.  1.READ X
 2.IF X=1 THEN END
 3.IF X=2 THEN DIVIDE X BY 0
 4.IF X>2 THEN GOTO STATEMENT 4
 We shall see in a moment that the same
terminology is applied to Turing machine.

5. ............
Read-Write head
Control Unit

6. ............
Read-Write head
No boundaries -- infinite length
The head moves Left or Right

7. ............
Read-Write head
The head at each transition (time step):
1. Reads a symbol
2. Writes a symbol
3. Moves Left or Right

8. ............
Example:
Time 0
............
Time 1
1. Reads
2. Writes
a a cb
a b k c
a
k
3. Moves Left

9. ............
Time 1
a b k c
............
Time 2
a k cf
1. Reads
2. Writes
b
f
3. Moves Right

10. ............ ◊ ◊ ◊ ◊
Blank symbol
head
◊a b ca
Head starts at the leftmost position
of the input string
Input string

11. 1q 2qLba ,→
Read Write
Move Left
1q 2qRba ,→
Move Right

12.  Definition. A Turing machine is a 7-tuple (Q, ∑, Γ, ∂,
q0, qaccept, qreject),
 where:
• Q is a set of states
∀ ∑ is a set of symbols (the alphabet)
∀ Γ is a set of symbols that can be written in tape, ∈
Γ and ∑ ⊆ Γ
• q0 ∈ Q is the initial state

13. • qaccept is the accepting state
• qreject is the rejecting state, qreject ≠ qaccept
∀ ∂ is a collection of transitions defined by the
function:
 ∂: (Q − {qaccept, qreject }) × Γ  Q × Γ × {, }

14. The machine halts in a state if there is
no transition to follow

15. Halting Example 1:
............ ◊ ◊ ◊ ◊◊a b ca
1q
1q No transition from
HALT!!!
1q

16. 1q 2q Allowed
1q 2q Not Allowed
•Accepting states have no outgoing transitions
•The machine halts and accepts

17. Accept Input
If machine halts
in an accept state
Reject Input
If machine halts
in a non-accept state
or
If machine enters
an infinite loop
string
string

18. Accepts the language: *a
0q
Raa ,→
L,◊→◊
1q
Input alphabet },{ ba=Σ

19. ◊ ◊ ◊ ◊aaTime 0
0q
a
0q
Raa ,→
L,◊→◊
1q

20. ◊ ◊ ◊ ◊aaTime 1
0q
a
0q
Raa ,→
L,◊→◊
1q

21. ◊ ◊ ◊ ◊aaTime 2
0q
a
0q
Raa ,→
L,◊→◊
1q

22. ◊ ◊ ◊ ◊aaTime 3
0q
a
0q
Raa ,→
L,◊→◊
1q

23. ◊ ◊ ◊ ◊aaTime 4
1q
a
0q
Raa ,→
L,◊→◊
1q
Halt & Accept

24. Rejection Example
0q
Raa ,→
L,◊→◊
1q
◊ ◊ ◊ ◊baTime 0
0q
a

25. 0q
Raa ,→
L,◊→◊
1q
◊ ◊ ◊ ◊baTime 1
0q
a
No possible Transition
Halt & Reject

26. Accepts the language: *a
0q
but for input alphabet }{a=Σ
A simpler machine for same language

27. ◊ ◊ ◊ ◊aaTime 0
0q
a
0q
Halt & Accept
Not necessary to scan input

32.  Turing machine as a language recognizer.
 Turing machine as a language generator.
 Turing machine as a language evaluator.
 Turing machine as a language decider.

33. ANY QUESTIONS??