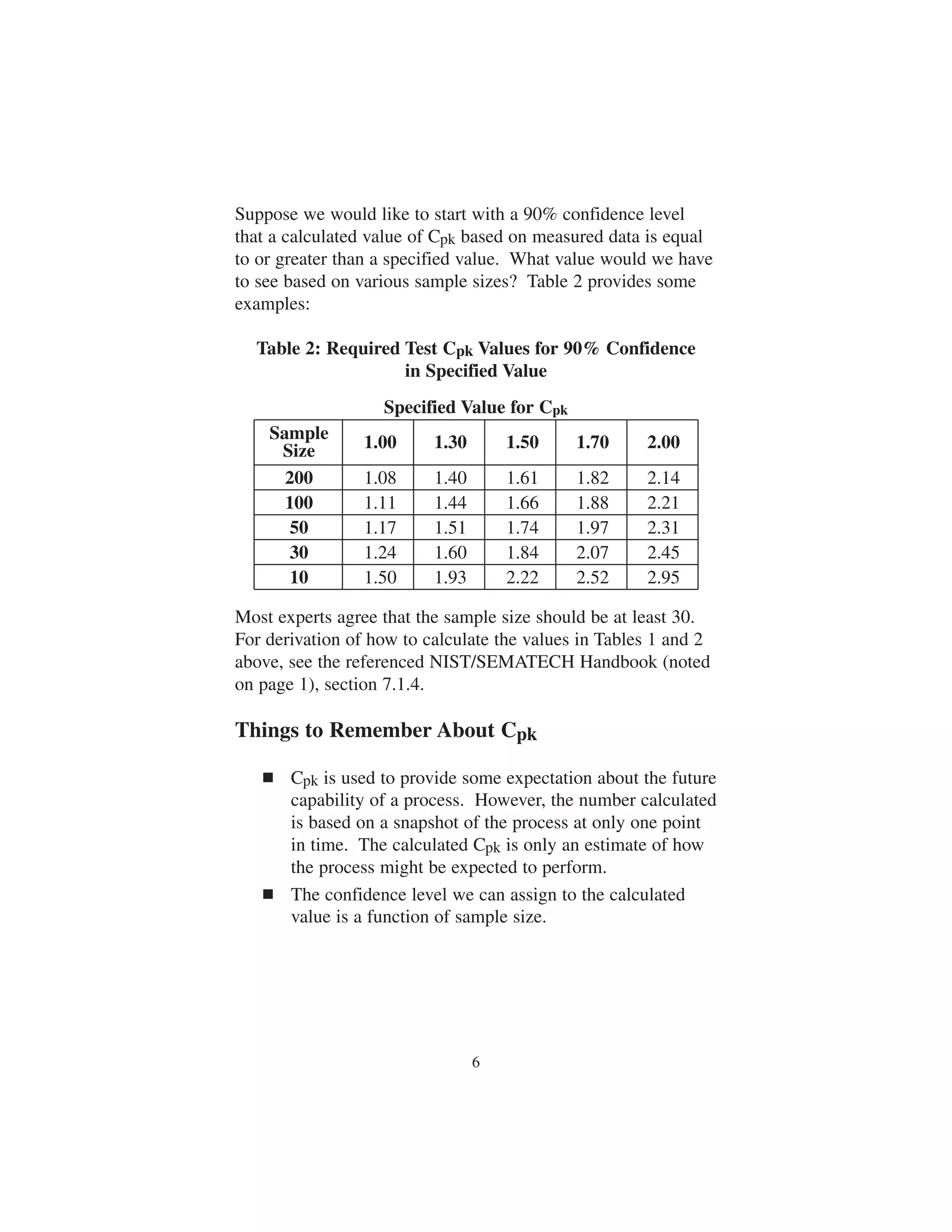
This document provides guidance on calculating and interpreting the process capability index Cpk. It defines Cpk as a ratio that compares the specification tolerance to the process variation expressed in terms of standard deviations. It explains how to calculate Cpk and discusses factors that influence Cpk values such as sample size, process centering, and measurement uncertainty. The document also provides examples of the expected defective parts per million that correspond to different Cpk values and factors to consider when improving Cpk, such as machine, tooling, workholding, and workpiece variables.

1. Cpk A Guide to Using Cpk
a Process Capability Index
LSL
Cpk = Min [ U S L , ] _ X X _LSL
3s 3s
Specification Width
Process Spread
X USL

2. The following information is provided by the
Technology Issues Committee of AMT –
The Association For Manufacturing Technology
to assist in the use and understanding of the
Process Capability Index Cpk.
Published by:
AMT – The Association For Manufacturing Technology
7901 Westpark Drive, McLean, VA 22102
Printed in the United States of America
Copyright © 2002 AMT – The Association For Manufacturing
Technology all rights reserved. Permission to photocopy this
material is granted provided credit is given to AMT.
For ordering information, see the Publication section of the
AMT Website at www.AMTonline.org or contact the AMT
Information Resource Center (IRC) at 703-827-5220 or
703-893-2900.

3. 11/02-PS150
7901 Westpark Drive, McLean, VA 22102-4206
Phone 703-893-2900 Fax 703-893-1151
AMT@AMTonline www.AMTonline.org

4. A Guide to Using Cpk
a Process Capability Index
1
Introduction
The purpose of this guide is twofold. The first is to provide
information on the process capability index Cpk. The second is
to list various actions that can be taken or parameters checked
in order to reduce process variation.
The idea of comparing the specification of a part parameter to
the measured variation or distribution of the process producing
the parameter has been with us for many years. It has only
been in recent years that the comparison has been given a for-mal
name and a means of calculation.
All authors and analysts writing on Cpk hasten to point out that
the index is a statistic based on measurements and, like all such
statistics, has an associated degree of uncertainty. However,
most practitioners consider Cpk to be a fixed number without
regard to the nature of the data that produced it. We will point
out the uncertainty involved in any statement of Cpk.
This guide assumes the reader has knowledge of control charts
and methods for calculating standard deviations. A good refer-ence
is the NIST/SEMATECH Handbook of Statistical Methods.
The complete Handbook is on the Internet and may be accessed
at www.itl.nist.gov/div898/handbook.
What is Cpk?
Cpk is a Process Capability Index. The term index is used
because the value is a comparison or ratio. It is the ratio of the

5. workpiece specification or tolerance (allowed variation) com-pared
to the process variation (produced variation) expressed in
terms of ± 3 standard deviations. When standard deviation is
used in a calculation, the assumption is that the underlying
measurements form a normal distribution.
Therefore, in the case of calculating Cpk, all known assignable
causes for variation in the process should be minimized before
measurements are taken that will be used in the final calcula-tion.
In other words, the process should be stable and in statis-tical
control.
Some processes may use a positive stop or an in-process gage
to produce part size. In those cases, the size distribution may
not be normal, and the calculations described here will not be
valid. Other sources should be consulted on how to deal with
skewed distributions.
In other cases, the specification is not bimodal nor is it given as
a range. Examples might be “hardness at least – ” or “surface
finish not to exceed –.” In those situations a Cpk cannot be cal-culated
since the part specification is not stated as a range. Of
course, the standard deviation for the process output can still be
calculated, and an estimate made about the probability of stay-ing
within the specification. But this is not a comparison such
as Cpk.
The importance of sample size in acquiring data cannot be over
emphasized. As we shall see, the calculated value of Cpk
depends on what is technically termed an “estimate” of the
standard deviation. The larger the sample size, the more accu-rate
is the estimate.
2

6. Calculating Cpk
Once data on the process has been gathered and analyzed, and
the standard deviation calculated, a comparison to the product’s
specification can be made. This simple comparison yields the
process potential Cp. In some cases, the mean of the process is
at the center of the product’s specification limit as shown in
Figure 1. The term Cp assumes centering and should be equal
to or greater than 1.
Specification Width
−
Process Spread
Specificat ion Pr s
USL is the upper specification limit
LSL is the lower specification limit
X is the process mean
Note: The symbol σ is used for standard deviation when very
large samples are used that accurately represent the total popu-lation.
In most cases, it is not feasible to use large samples,
and the resultant standard deviation is represented by s.
3
=
ocess USL LSL
6
Cp =

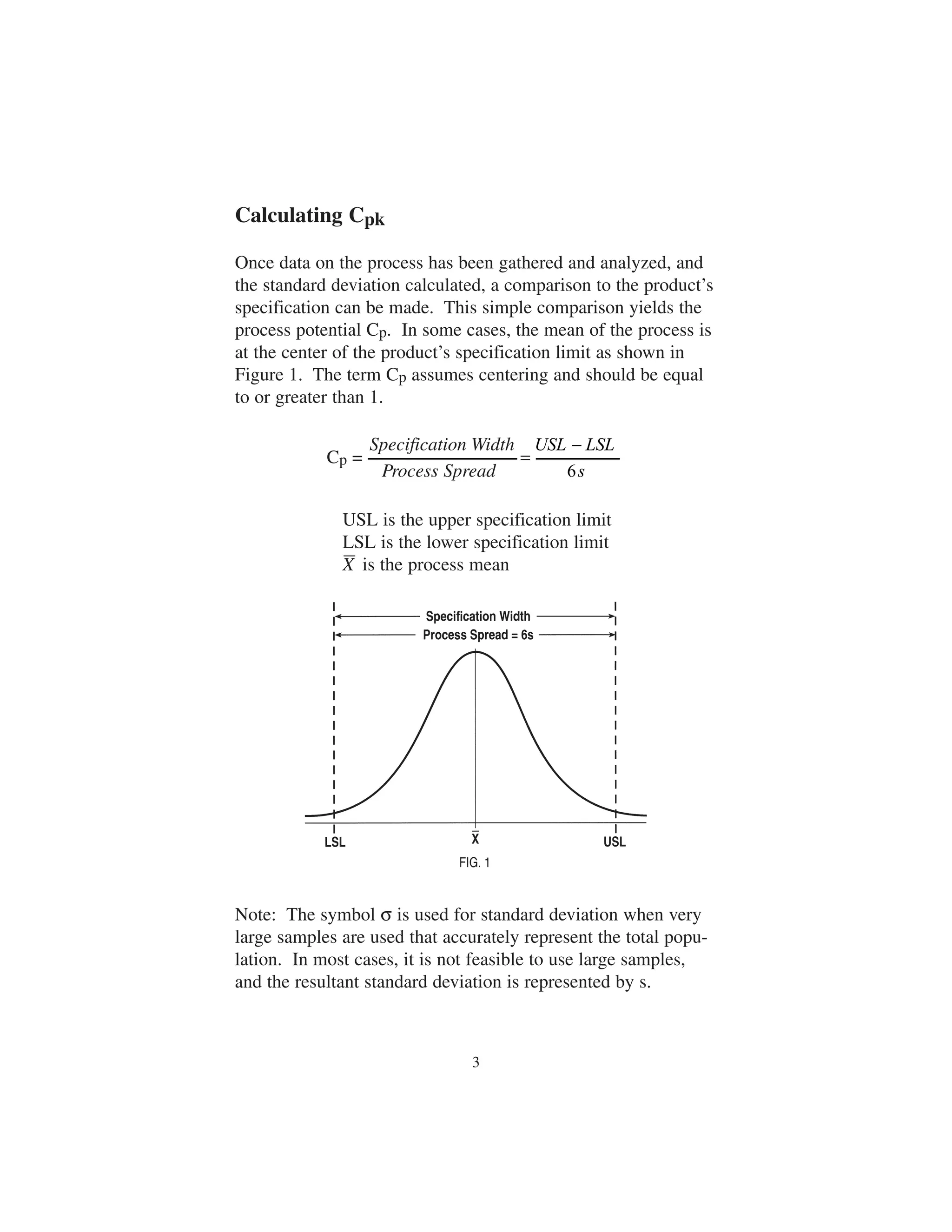
7. However, in most cases, the process will not be centered on the
specification as shown in Figure 2. The actual process capabili-ty
Cpk then becomes
X Nearest Specificat ion Limit
X Nearest Specification Limit
USL X
−
X LSL
In Figure 2, the nearest specification limit is USL. An
inspection of Figure 2 will show that the first step in increasing
Cpk should be to take action to align the center of the process
spread with the center of the specification spread. This
assumes that the two spreads are close to equal, or the process
spread is actually less than the specification spread.
4
s
3
−
s
3
−
s
3
Cpk =
This is usually stated as
Cpk = Min [ , ]
FIG. 2

8. Of course, if the process spread greatly exceeds the specifica-tion
spread, steps must be taken to reduce the process spread.
In Figure 2, Cpk would be about 0.5. However, if the process
spread were aligned with the specification, Cpk would be about
1.0.
Putting Cpk in Perspective
For the sake of simplicity, let’s assume that the process is cen-tered
on the product specification. How many defective parts
per million (parts out of tolerance) would we expect for differ-ent
values of Cpk? Table 1 lists some values:
Table 1: Expected number of defective parts
for values of Cpk
Cpk Parts per million defective
1.00 2,700.0
1.10 967.0
1.20 318.0
1.30 96.0
1.40 26.0
1.50 6.8
1.60 1.6
1.70 0.34
1.80 0.06
2.00 0.0018
It should be noted that a Cpk of 2 equates to roughly two parts
per billion defective! Such a number highlights the signifi-cance
of sample size and the related issue of uncertainty associ-ated
with the actual value of Cpk.
5

9. Suppose we would like to start with a 90% confidence level
that a calculated value of Cpk based on measured data is equal
to or greater than a specified value. What value would we have
to see based on various sample sizes? Table 2 provides some
examples:
Table 2: Required Test Cpk Values for 90% Confidence
in Specified Value
Specified Value for Cpk
Sample
Size 1.00 1.30 1.50 1.70 2.00
200 1.08 1.40 1.61 1.82 2.14
100 1.11 1.44 1.66 1.88 2.21
50 1.17 1.51 1.74 1.97 2.31
30 1.24 1.60 1.84 2.07 2.45
10 1.50 1.93 2.22 2.52 2.95
Most experts agree that the sample size should be at least 30.
For derivation of how to calculate the values in Tables 1 and 2
above, see the referenced NIST/SEMATECH Handbook (noted
on page 1), section 7.1.4.
Things to Remember About Cpk
Cpk is used to provide some expectation about the future
capability of a process. However, the number calculated
is based on a snapshot of the process at only one point
in time. The calculated Cpk is only an estimate of how
the process might be expected to perform.
The confidence level we can assign to the calculated
value is a function of sample size.
6

10. We should not lose sight of the fact that establishing process
capability gives us a benchmark for improvement. Continuous
improvement is the ultimate goal of making the measurements.
Factors to Consider in Improving Cpk
Measurement
The key element in establishing Cpk with a customer is reach-ing
agreement on the measurement method and gauges to be
used. The condition of the measurement equipment, and gauge
reproducibility and repeatability (RR) should be stated. In
fact, for tight tolerances, the conditions used to determine RR
should be stated – such as the number of appraisers and the
number of repeat measurements. In order to be able to analyze
data for events that happen during a test run, make sure that
measurements are recorded chronologically.
See Section 2.4 in the NIST/SEMATECH referenced Handbook
for a complete discussion on gauge RR.
Machine
Thermal deformation is one of the greatest contributors to
change in the output of a machine tool. All elements respond-ing
to temperature change should be understood and monitored.
Machine accuracy and repeatability should be determined using
statistical techniques. Factors such as alignment, spindle
runout and balance, and dynamic stability should be accessed
with respect to the contribution to desired workpiece parame-ters.
Machine maintenance is useful to restore parameters that have
deteriorated and are contributing to variations. Company pro-cedures
should be established for maintaining machine calibra-tion.
7

11. Tooling
Changes in tool condition are a common source of shift in
workpiece size or surface finish. These changes can best be
analyzed from a histogram of data taken chronologically.
Changes are not limited to tool wear, but may also be created
by dirt on the toolholder, a balance condition, or repeatability
when changing inserts.
Workholding
The ability of the workholding device to position each part con-sistently
is critical to maintaining uniform output. Tests should
be made to determine the repeatability of workholding devices.
The rigidity of the workholding device in relation to the rigidity
of the workpiece and process-induced forces can also influence
size variation.
Workpiece
Variations in workpiece initial stock conditions are a common
source of output variation. Workpieces should be checked for
incoming size and hardness. Both parameters cause changes in
process forces. Cpk of incoming parts would be desirable.
8