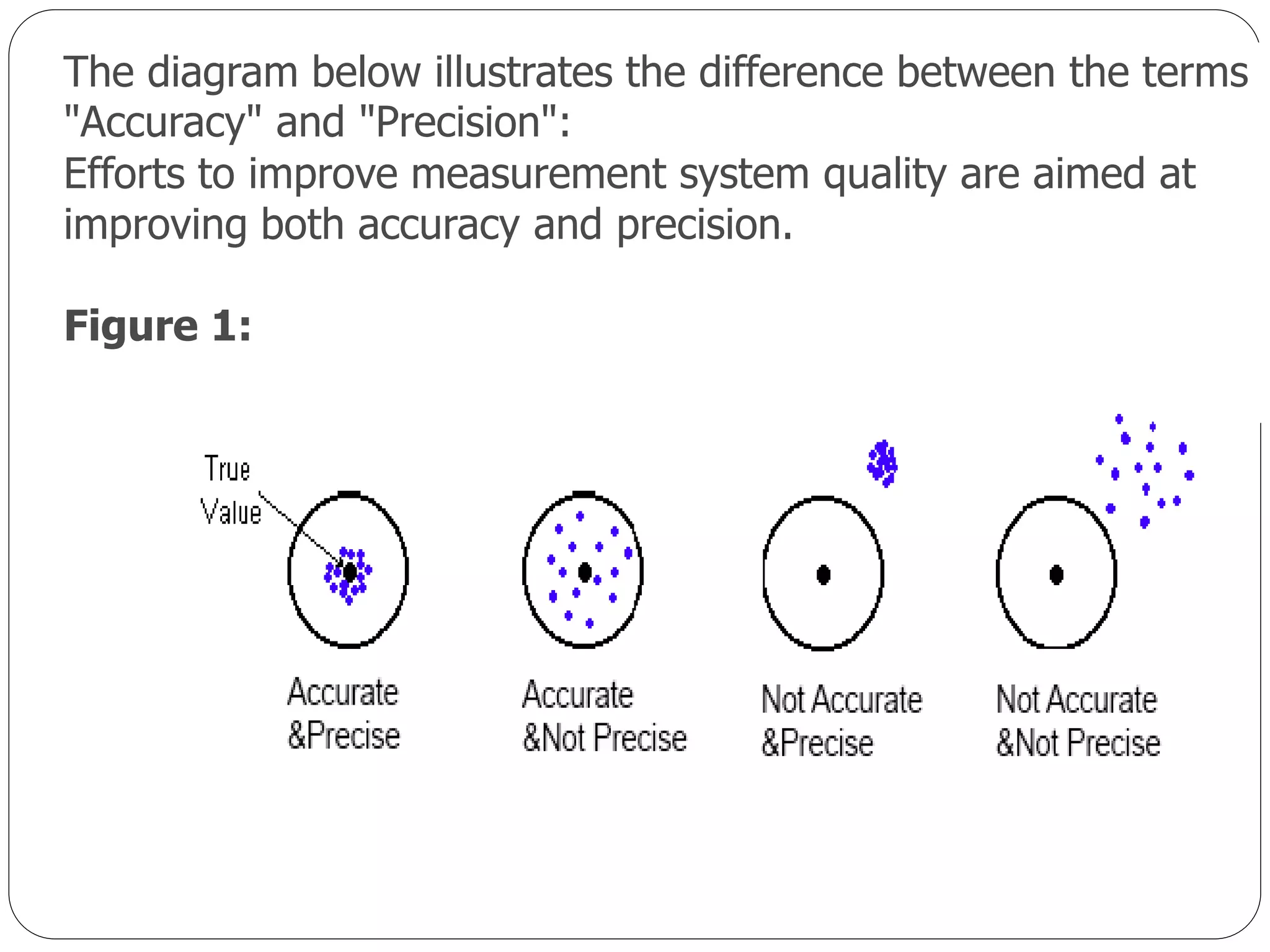
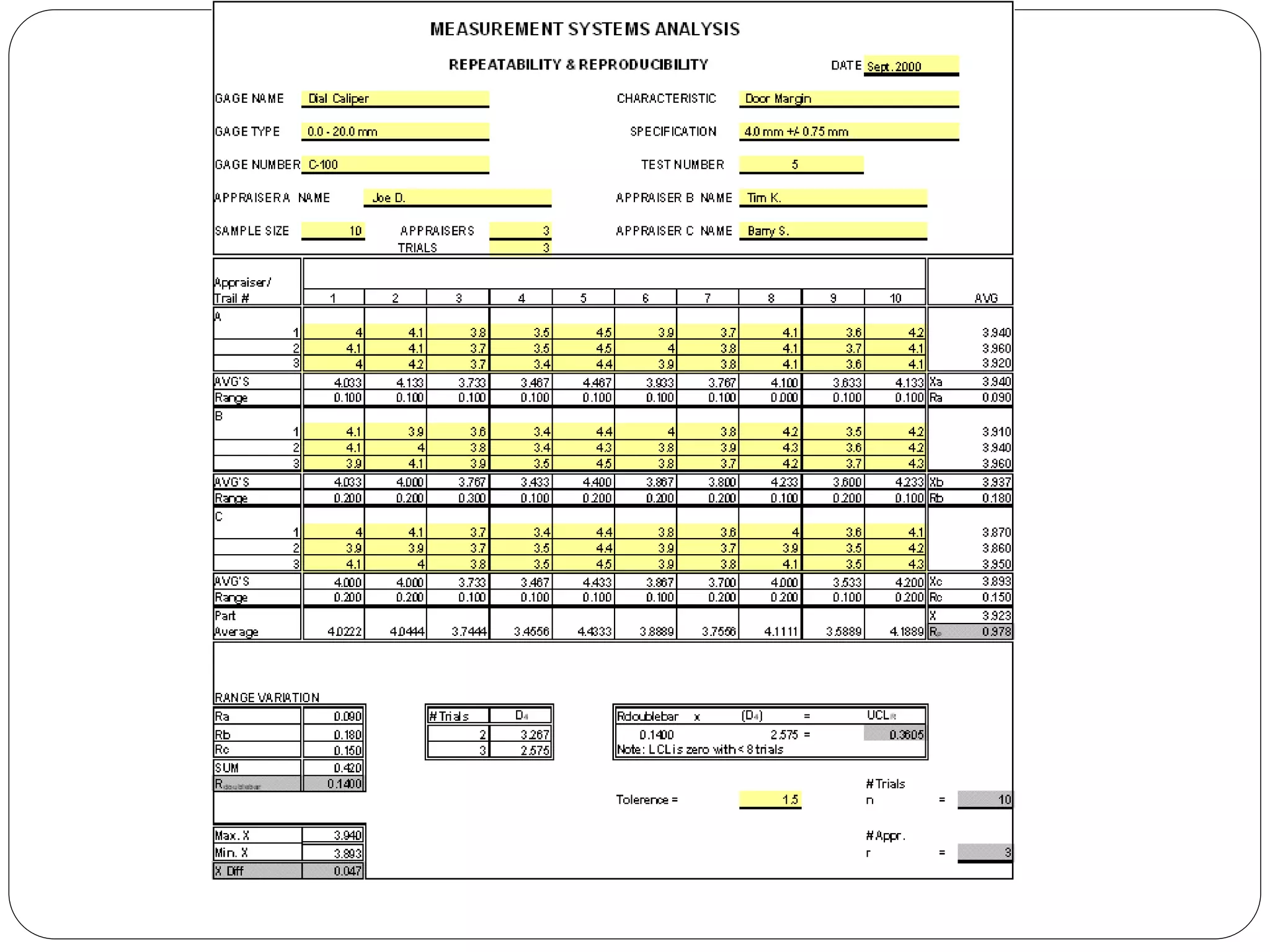
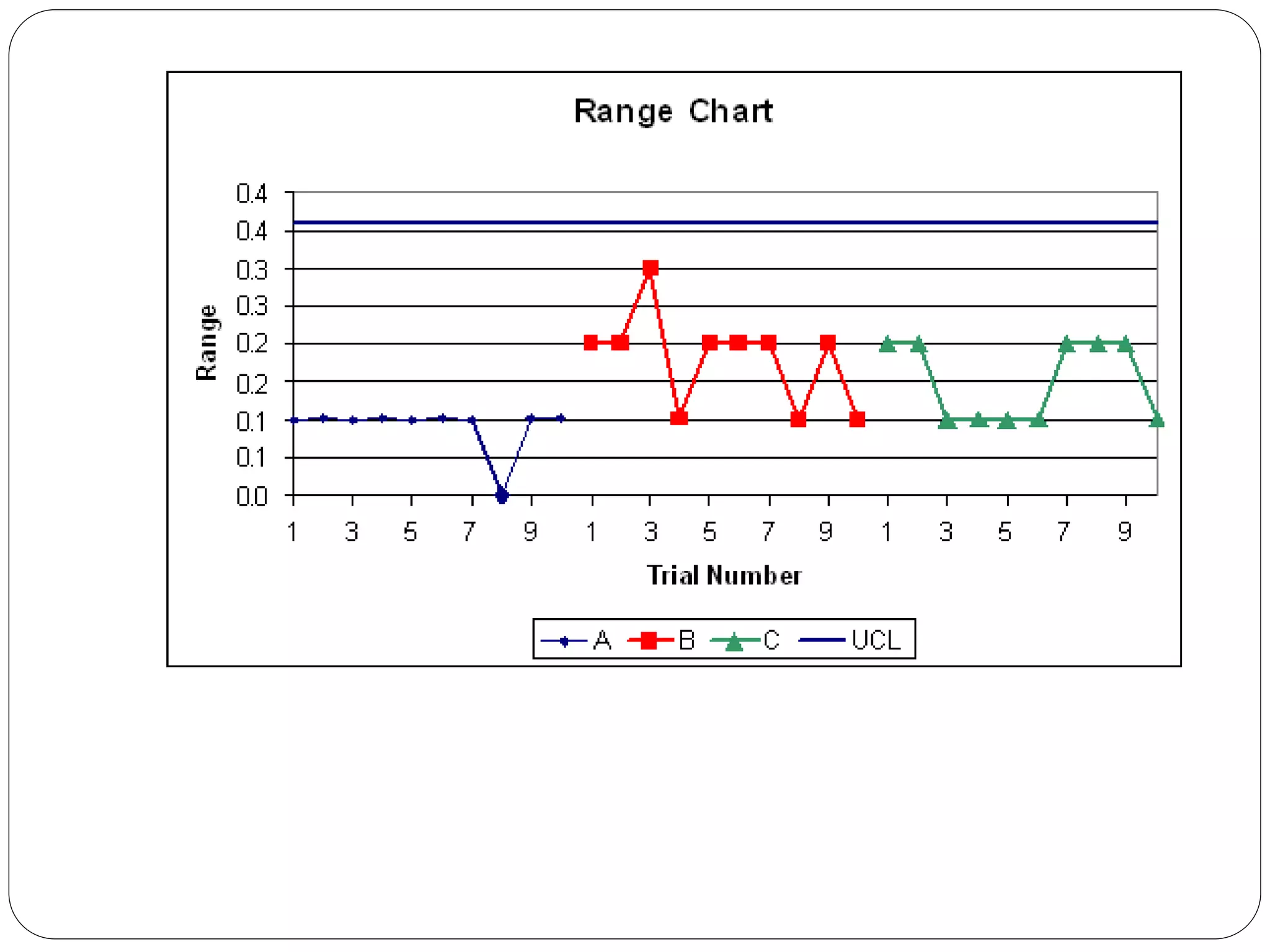
This document defines key concepts in measurement system analysis including accuracy, precision, stability, bias, repeatability, and reproducibility. It provides guidelines for conducting a measurement system analysis, including determining the number of appraisers and parts to measure, ensuring the measurement procedure is documented and followed, and analyzing the results in terms of stability, bias, and gauge R&R to determine if the measurement system is capable and can be used for decision making. The goal is to qualify measurement systems and identify opportunities for improvement.

1. By
S.RAMKUMAR
PRAGYA CONSULTANCY
Email: ramkumarsm@gmail.com
Measurement System Analysis
(MSA)

2. Purpose
 The purpose of Measurement System
Analysis is to qualify a measurement system
for use by quantifying its
 accuracy,
 precision, and
 stability.

3. A measurement system can be
characterized, or described, in five ways:
Location (Average Measurement Value vs.
Actual Value):
 Stability
 Bias
 Linearity
Variation (Spread of Measurement Values -
Precision):
 Repeatibility
 Reproducibility

4. Location (Average Measurement Value
vs. Actual Value):
 Stability refers to the capacity of a measurement
system to produce the same values over time when
measuring the same sample. As with statistical
process control charts, stability means the absence of
"Special Cause Variation", leaving only "Common
Cause Variation" (random variation).
 Bias, also referred to as Accuracy, is a measure of
the distance between the average value of the
measurements and the "True" or "Actual" value of the
sample or part.
 Linearity is a measure of the consistency of Bias
over the range of the measurement device. For
example, if a bathroom scale is under by 1.0 pound
when measuring a 150 pound person, but is off by 5.0
pounds when measuring a 200 pound person, the
scale Bias is non-linear in the sense that the degree
of Bias changes over the range of use.

5. Variation (Spread of Measurement
Values - Precision):
 Repeatability assesses whether the same
appraiser can measure the same part/sample
multiple times with the same measurement device
and get the same value.
 Reproducibility assesses whether different
appraisers can measure the same part/sample
with the same measurement device and get the
same value.

6. The diagram below illustrates the difference between the terms
"Accuracy" and "Precision":
Efforts to improve measurement system quality are aimed at
improving both accuracy and precision.
Figure 1:

7. Requirements
 Statistical stability over time.
 Variability small compared to the process variability.
 Variability small compared to the specification limits
(tolerance).
 The resolution, or discrimination of the measurement
device must be small relative to the smaller of either
the specification tolerance or the process spread
(variation). As a rule of thumb, the measurement
system should have resolution of at least 1/10th the
smaller of either the specification tolerance or the
process spread. If the resolution is not fine enough,
process variability will not be recognized by the
measurement system, thus blunting its effectiveness.

8. Measurement Systems Analysis
Fundamentals
 Determine the number of appraisers, number of
sample parts, and the number of repeat readings.
Larger numbers of parts and repeat readings give
results with a higher confidence level, but the
numbers should be balanced against the time, cost,
and disruption involved.
 Use appraisers who normally perform the
measurement and who are familiar with the
equipment and procedures.
 Make sure there is a set, documented measurement
procedure that is followed by all appraisers.
 Select the sample parts to represent the entire
process spread. This is a critical point. If the process
spread is not fully represented, the degree of
measurement error may be overstated.

9. Measurement Systems Analysis
Fundamentals
 If applicable, mark the exact measurement
location on each part to minimize the impact of
within-part variation (e.g. out-of-round).
 Ensure that the measurement device has
adequate discrimination/resolution, as discussed
in the Requirements section.
 Parts should be numbered, and the
measurements should be taken in random order
so that the appraisers do not know the number
assigned to each part or any previous
measurement value for that part. A third party
should record the measurements, the appraiser,
the trial number, and the number for each part on
a table.

10. Stability Assessment
 Select a part from the middle of the process spread and
determine its reference value relative to a traceable
standard. If a traceable standard is not available, measure
the part ten times in a controlled environment and average
the values to determine the Reference Value. This
part/sample will be designated as the Master Sample .
 Over at least twenty periods (days/weeks), measure the
master sample 3 to 5 times. Keep the number of repeats
fixed. Take readings throughout the period to capture the
natural environmental variation.
 Plot the data on an x̄ & R chart - consult the Statistical
Process Control section of the Toolbox and calculate
control limits.
 Evaluate the control chart for statistical control. Again,
consult the Statistical Process Control section of the
Toolbox for assistance with this assessment.

11. Bias Assessment
 Referring to the & R chart, subtract the Reference
Value from to yield the Bias:
Bias = x̄ - Reference Value
Process Variation = 6 Standard Deviations
(Sigma)
 Calculate the Bias percentage:
Bias Percentage = Bias / Process Variation

12. Bias Assessment
 Analyze the results. If there is a relatively high
value, examine the following potential root
causes: Appraisers not following the
measurement procedure
 An error in measuring the Reference Value
 Instability in the measurement. If the SPC chart
shows a trend, the measurement device could be
wearing or calibration could be drifting.

13. Repeatability and Reproducibility
Assessment (Gage R&R):
Follow the steps below to conduct a Gage R&R study:
 Determine the number of appraisers, trials, and parts,
which may vary from study to study. A rule of thumb is
2-3 appraisers, 2-3 trials, and 5-10 parts - with 10
being greatly preferred. The downloadable
MoreSteam.com spreadsheet will accommodate any
combination within this range. In this example we will
use 2 appraisers, 3 trials, and 10 parts.
 Identify three appraisers who are all trained in the
proper measurement procedure and identify them as
A, B & C.
 Fill in the yellow blanks at the top of the form with the
required background information (Gage Type, Date,
etc.). Also fill in the blank at the bottom of the form
asking for the total specification tolerance.

14. Repeatability and Reproducibility
Assessment (Gage R&R):
 Collect ten parts that represents the range of process
variation. If the parts don't vary as much as the
process, the gage error will be overstated.
 Identify each part with a number 1-10 in such a way
that the appraisers can not see the numbers as they
take the measurements.
 Please refer to the data collection chart below. You
will see that appraiser A's three trials are recorded in
rows A-1, A-2, and A-3. Likewise, Appraiser B has
rows B-1, B-2, and B-3, and Appraiser C has rows C-
1, C-2, and C-3.
 Start with Appraiser A and measure each of the ten
parts in random order. A third party should record the
results of the first trial in row A-1. Proceed to
Appraisers B & C following the same process. Then
repeat the process for trials two and three.

17. Thumb rule
 The rule of thumb for acceptance of a
measurement system is a total Gage R&R of 30%
or less of the lessor of Total Variation or the
Specification Tolerance. In this case, the
measurement system is capable, and can be
used as a basis of decision making.
 If the measurement system has error in excess of
30%, the first step to improve results is to analyze
the breakdown of the error source. If the largest
contributor to error is Repeatability, then the
equipment must be improved. Likewise, if
Reproducibility is the largest source of error,
appraiser training and adherence to procedures
can yield improvement.

18. Summary
 Measurement Systems Analysis is a key step to
any process improvement effort.
 By understanding existing measurement systems
a team can better understand the data provided
by those systems and make better business
decisions.