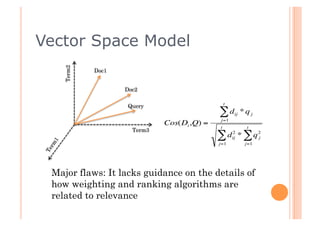
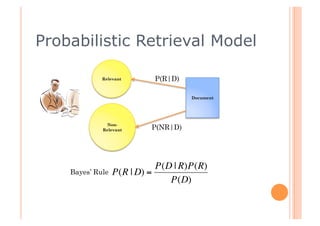
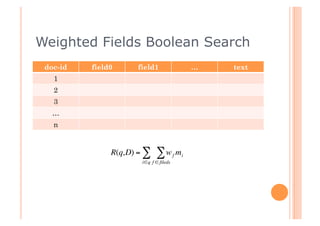
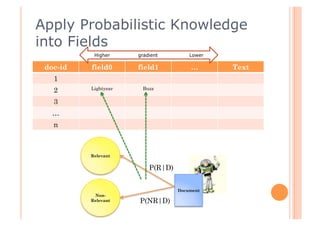
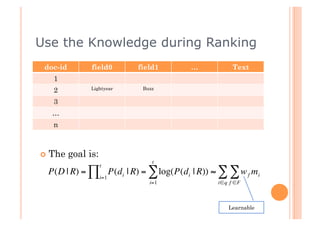
This document discusses incorporating probabilistic retrieval knowledge into TFIDF-based search engines. It provides an overview of different retrieval models such as Boolean, vector space, probabilistic, and language models. It then describes using a probabilistic model that estimates the probability of a document being relevant or non-relevant given its terms. This model can be combined with the BM25 ranking algorithm. The document proposes applying probabilistic knowledge to different document fields during ranking to improve relevance.

1. INCORPORATING
PROBABILISTIC
RETRIEVAL
KNOWLEDGE INTO
TFIDF-BASED SEARCH
ENGINE
Alex Lin
Senior Architect
Intelligent Mining
alin at IntelligentMinining.com

2. Overview of Retrieval Models
 Boolean Retrieval
 Vector Space Model
 Probabilistic Model
 Language Model

3. Boolean Retrieval
 lincolnAND NOT (car AND automobile)
 The earliest model and still in use today
 The result is very easy to explain to users
 Highly efficient computationally
 The major drawback – lack of sophisticated
ranking algorithm.

4. Vector Space Model
Term2 Doc1
Doc2
t
Query
∑d ij *qj
j=1
Cos(Di ,Q) =
t t
Term3
∑ d * ∑q2
ij
2
j
j=1 j=1
Major flaws: It lacks guidance on the details of
€
how weighting and ranking algorithms are
related to relevance

5. Probabilistic Retrieval Model
Relevant P(R|D)
Document
Non-
Relevant P(NR|D)
P(D | R)P(R)
Bayes’ Rule P(R | D) =
P(D)
€

6. Probabilistic Retrieval Model
P(D | R)P(R) P(D | NR)P(NR)
P(R | D) = P(NR | D) =
P(D) P(D)
 IfP(D | R)P(R) > P(D | NR)P(NR)
€ €
then classify D as relevant
€

7. Estimate P(D|R) and P(D|NR)
 Define D = (d1,d2 ,...,dt )
t
then P(D | R) = ∏ P(di | R)
i=1
t
€ P(D | NR) = ∏ P(di | NR)
i=1
€
 Binary Independence Model
€ term independence + binary features in documents

8. Likelihood Ratio
 Likelihood ratio:
P(D | R) P(NR)
>
P(D | NR) P(R)
si: in non-relevant set, the probability of term i occurring
pi: in relevant set, the probability of term i occurring
P(D | R) pi 1− pi pi (1− si )
=∏ ⋅ ∏ = ∑ log
€ P(D | NR) i:d i =1 si i:d i = 0 1− si i:d i =1 si (1− pi )
(ri + 0.5) /(R − ri + 0.5)
= ∑ log
i:d i = q i =1 (n i − ri + 0.5) /(N − n i − R + ri + 0.5)
€
N: total number of Non-relevant documents
ni: number of non-relevant documents that contain a term
ri: number of relevant documents that contain a term
R: total number of Relevant documents
€

9. Combine with BM25 Ranking
Algorithm
 BM25 extends the scoring function for the binary
independence model to include document and
query term weight.
 It performs very well in TREC experiments
(ri + 0.5) /(R − ri + 0.5) (k + 1) f i (k 2 + 1)qf i
R(q,D) = ∑ log ⋅ i ⋅
i∈Q
(n i − ri + 0.5) /(N − n i − R + ri + 0.5) K + f i k 2 + qf i
dl
K = k1 ((1− b) + b ⋅ )
avgdl
€
k1 k2 b: tuning parameters
dl: document length
avgdl: average document length in data set
€
qf: term frequency in query terms

10. Weighted Fields Boolean Search
doc-id field0 field1 … text
1
2
3
…
n
R(q,D) = ∑ ∑w f mi
i∈q f ∈ fileds
€

11. Apply Probabilistic Knowledge
into Fields
Higher gradient Lower
doc-id field0 field1 … Text
1
Lightyear Buzz
2
3
…
n
Relevant
P(R|D)
Document
Non-
Relevant P(NR|D)

12. Use the Knowledge during Ranking
doc-id field0 field1 … Text
1
Lightyear Buzz
2
3
…
n
 The goal is:
t
t
P(D | R) = ∏ P(di | R) = ∑ log(P(di | R)) ≈ ∑ ∑ w f mi
i=1
i=1 i∈q f ∈F
Learnable
€

13. Comparison of Approaches
f ik N
RTF −IDF = tf ik ⋅ idf i = t
⋅ log
nk
∑f ij
j=1
(k1 + 1) f i (k2 + 1)qf i dl
Rbm 25 (q,D) = ⋅ K = k1 ((1− b) + b ⋅ )
K + fi k 2 + qf i avgdl
€ (ri + 0.5) /(R − ri + 0.5) (k + 1) f i (k 2 + 1)qf i
R(q,D) = ∑ log ⋅ 1 ⋅
i∈Q
(n i − ri + 0.5) /(N − n i − R + ri + 0.5) K + f i k 2 + qf i
€ €
IDF TF
€ (k1 + 1) f i (k 2 + 1)qf i
R(q,D) = ∑ ∑ w f mi ⋅ ⋅
i∈q f ∈F K + fi k 2 + qf i
IDF TF
€

14. Other Considerations
 Thisis not a formal model
 Require user relevance feedback (search log)
 Harder to handle real-time search queries
 How to Prevent Love/Hate attacks

15. Thank you